The capacitance in an oscilatory LC circuit is increased by 1%. The charge in inductance required to restore its frequency of oscillation is to
decrease it by 0.5%
increase it by 1%
decrease it by 1%
decrease it by 2%
The correct Answer is:C
To solve the problem, we need to analyze the relationship between capacitance (C), inductance (L), and the frequency of oscillation in an LC circuit.
1. Understanding the Frequency of Oscillation:
The frequency of oscillation f in an LC circuit is given by the formula:
f=12π√LC
where L is the inductance and C is the capacitance.
2. Effect of Increasing Capacitance:
According to the problem, the capacitance C is increased by 1%. Therefore, we can express the new capacitance C′ as:
C′=C+0.01C=1.01C
3. New Frequency Calculation:
Substituting C′ into the frequency formula gives us the new frequency f′:
f′=12π√L⋅1.01C
4. Setting the Frequencies Equal:
To restore the original frequency f, we need to adjust the inductance L. Let the new inductance be L′. The frequency with the new inductance and increased capacitance must equal the original frequency:
f=f′⇒12π√LC=12π√L′⋅1.01C
5. Squaring Both Sides:
Squaring both sides to eliminate the square roots gives:
1LC=1L′⋅1.01C
6. Cross Multiplying:
Cross multiplying leads to:
L′⋅1.01C=LC
7. Solving for New Inductance:
Dividing both sides by 1.01C gives:
L′=L1.01
8. Calculating the Change in Inductance:
The change in inductance ΔL can be calculated as:
ΔL=L′−L=L1.01−L=L(11.01−1)
Simplifying this expression:
ΔL=L(1−1.011.01)=L(−0.011.01)
9. Percentage Change in Inductance:
To find the percentage change in inductance:
Percentage Change=ΔLL×100=−0.011.01×100≈−0.9901%
This can be approximated to about -1%.
Conclusion:
The inductance must decrease by approximately 1% to restore the frequency of oscillation after the capacitance is increased by 1%.
Thus, the correct answer is option 3: decrease by 1%.
The frequency of oscillation f in an LC circuit is given by the formula:
f=12π√LC
where L is the inductance and C is the capacitance.
According to the problem, the capacitance C is increased by 1%. Therefore, we can express the new capacitance C′ as:
C′=C+0.01C=1.01C
Substituting C′ into the frequency formula gives us the new frequency f′:
f′=12π√L⋅1.01C
To restore the original frequency f, we need to adjust the inductance L. Let the new inductance be L′. The frequency with the new inductance and increased capacitance must equal the original frequency:
f=f′⇒12π√LC=12π√L′⋅1.01C
Squaring both sides to eliminate the square roots gives:
1LC=1L′⋅1.01C
Cross multiplying leads to:
L′⋅1.01C=LC
Dividing both sides by 1.01C gives:
L′=L1.01
The change in inductance ΔL can be calculated as:
ΔL=L′−L=L1.01−L=L(11.01−1)
Simplifying this expression:
ΔL=L(1−1.011.01)=L(−0.011.01)
To find the percentage change in inductance:
Percentage Change=ΔLL×100=−0.011.01×100≈−0.9901%
This can be approximated to about -1%.
The inductance must decrease by approximately 1% to restore the frequency of oscillation after the capacitance is increased by 1%.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (multiple Correct )7videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (assertion-reasoning)2videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (subjective)7videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type2videos
MAGNETIC FIELD AND MAGNETIC FORCES
Similar Questions
Knowledge Check
- Question 1 - Select One
The natural frequency (ω0) of oscillations in LC circuit is given by
A12π1√LCB1π1√2LCC1√LCD√LC
Two instruments having stretched strings are being played in unison . When the tension in one of the instruments is increases by 1%,3 beats are produced in 2s. The initial frequency of vibration of each wire is
View SolutionTwo instruments having stretched strings are being played in unison . When the tension in one of the instruments is increases by 1%,3 beats are produced in 2s. The initial frequency of vibration of each wire is
View SolutionA resistor R, an inductor L, a capacitor C and voltmeters V1,V2 and V3 are connected to an oscillator in the circuit as shown in the adjoining diagram.When the frequency of the oscillator is increased, upto resonance frequency, the voltmeter reading (at resonance frequency) is zero in the case of:
 View Solution
View SolutionInitially, the capacitor is charged to a potential of 5V and then connected to position 1 with the shown polarity for 1s. After 1s it is connected across the inductor at position 2
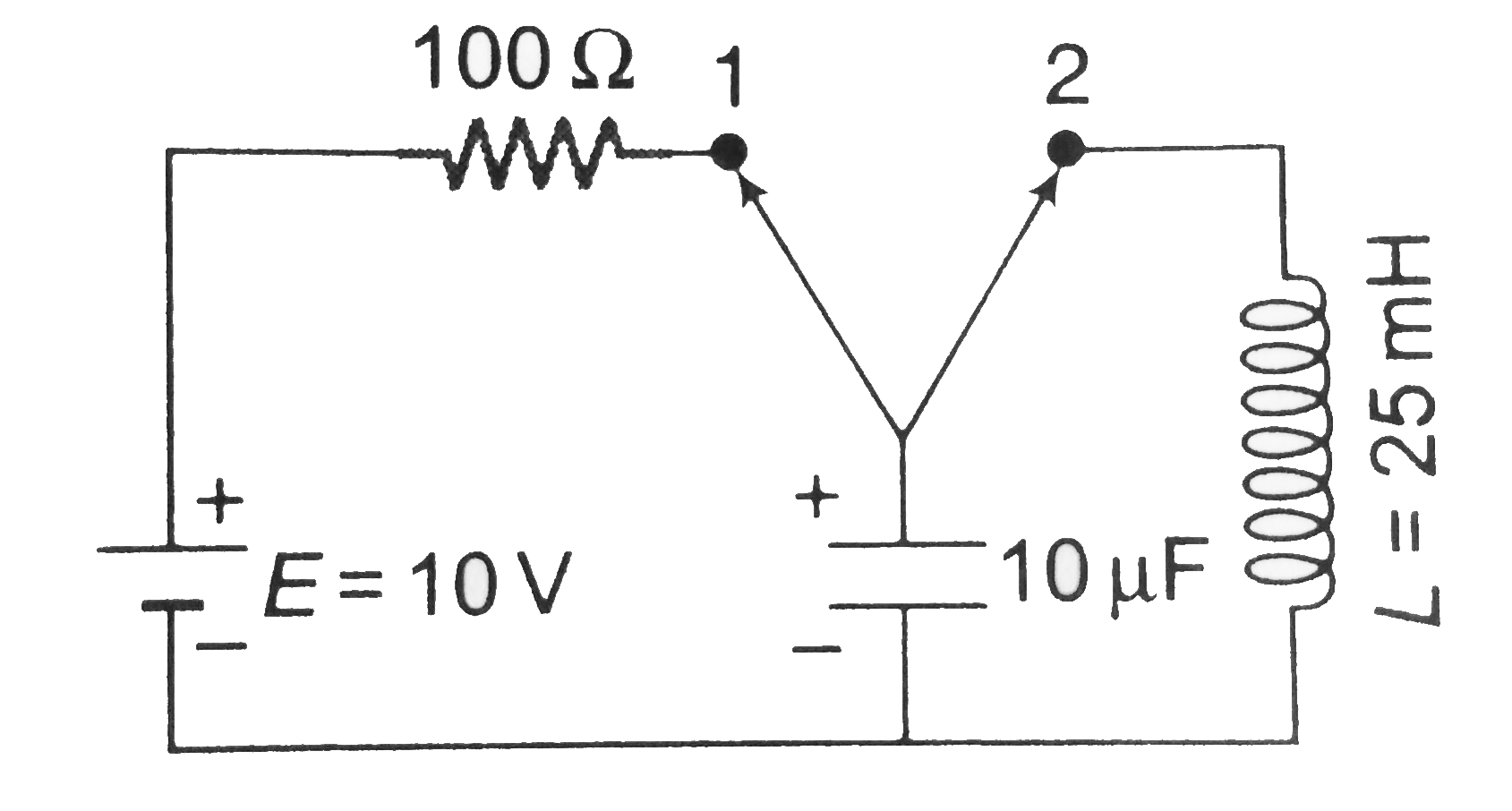
(a) Find the potential across the capacitor after 1s of its connection to position 1.
(b) Find the maximum current flowing in the L−C circuit when capacitor is connected across the inductor. Also, find the frequency of LC oscillations.View SolutionThe capacitance of a pure capacitance is 1 farad. In DC circuits, its effective resistance will be
View SolutionCapacitance of a conductor is 1μF. What charge is required to raise its potential to 100V?
View SolutionIn an alternating current circuit in which an inductance and capacitance are joined in series, current is found to be maximum when the value of inductance is 0.5 henry and the value of capacitance is 8µF. The angular frequency of applied alternating voltage will be
View Solution

