Initially, the capacitor is charged to a potential of 5V and then connected to position 1 with the shown polarity for 1s. After 1s it is connected across the inductor at position 2
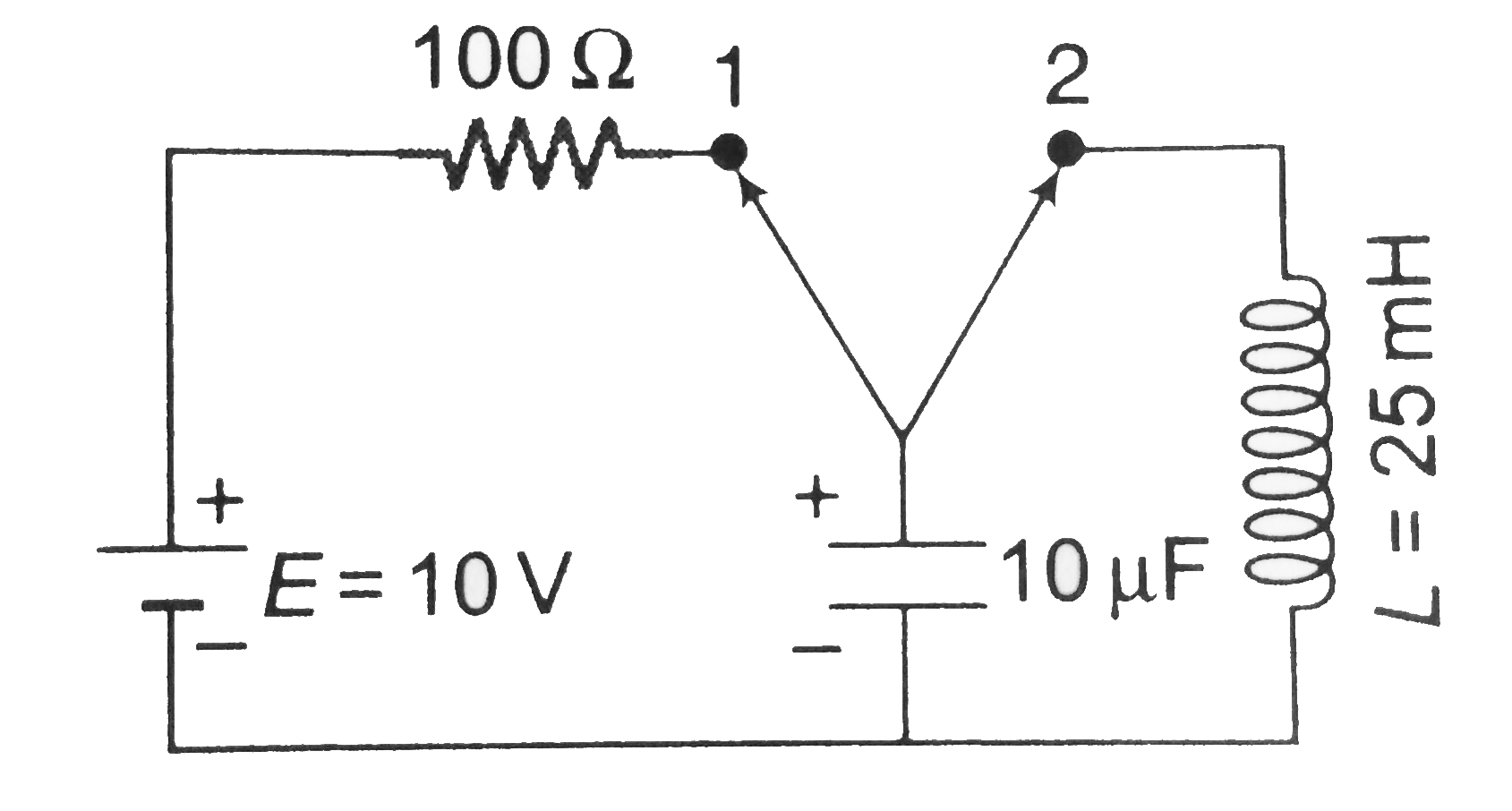
(a) Find the potential across the capacitor after 1s of its connection to position 1.
(b) Find the maximum current flowing in the L−C circuit when capacitor is connected across the inductor. Also, find the frequency of LC oscillations.
The correct Answer is:A
In the capacitor,
qi=CVi=(10×10−3)(5)=0.05C
qf=CVf=(10×10−3)(10)=0.1C
∴ Charge in capacitor will increase from 0.05C to 0.1C exponentialy.
Time constant for this increase would be
τL=CR=1s
∴ Charge at time t will be
q=0.05+(0.1−0.05)(1−e−t/τC)
=0.1−0.05e−t/τC
b. At t=1s,q=0.1−0.05e−1=0.0816C
V=qC=0.081610×10−3=8.16V
b. This charge 0.0816C is also the maximum charge q0 of L−C oscillations.
From energy conservation equation,
12q20C=12Li20 we have,
i0=q0√LC=0.0816√25×10−3×10×10−3
=5.16A
Further, ω=1√LCor f=ω2π=12π√LC
=12π√25×10−3×10×10−3
=10Hz
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example
71 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point
60 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - SUBJECTIVE TYPE
1 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
A capacitor of capacity 2μF is charged to a potential difference of 12V. It is then connected across an inductor of inductance 6μH. At an instant when potential difference across the capacitor is 6V, what is the current(in A)?
View SolutionA capacitor C is charged to a potential V by a battery. It is then disconnected from the battery and again connected with its polarity reversed to the battery
View Solution
Knowledge Check
Two idential capacitors are joined in parallel, charged to a potential V and then separated and then connected in series i.e. the positive plate of one is connected to negative of the other
AThe charges on the free plated connected together are destoyed.BThe energy stored in the system increases.CThe potential difference between the free plates is 2V.DThe potential difference remains constant.
A capacitor of capacity 2μF is changed to a potential different of 12V . It is then connected across an inductor of inductance 0.6mH What is the current in the circuit at a time when the potential difference across the capacitor is 6.0V ?
View SolutionA capacitor of capacity 2μF is changed to a potential different of 12V . It is then connected across an inductor of inductance 0.6mH What is the current in the circuit at a time when the potential difference across the capacitor is 6.0V ?
View SolutionHow many 1μF capacitors must be connected in parallel to store a charge of 1 C with a potential of 110 V across the capacitors?
View SolutionA 10μF capacitor is charged to 15V. It is next connected in seties with an uncharged 5μf capacitor. The series cambination is finally connected across a 30V battery, as shown in. Find the new potential differnce across the 5μF and 10μF capacitors.
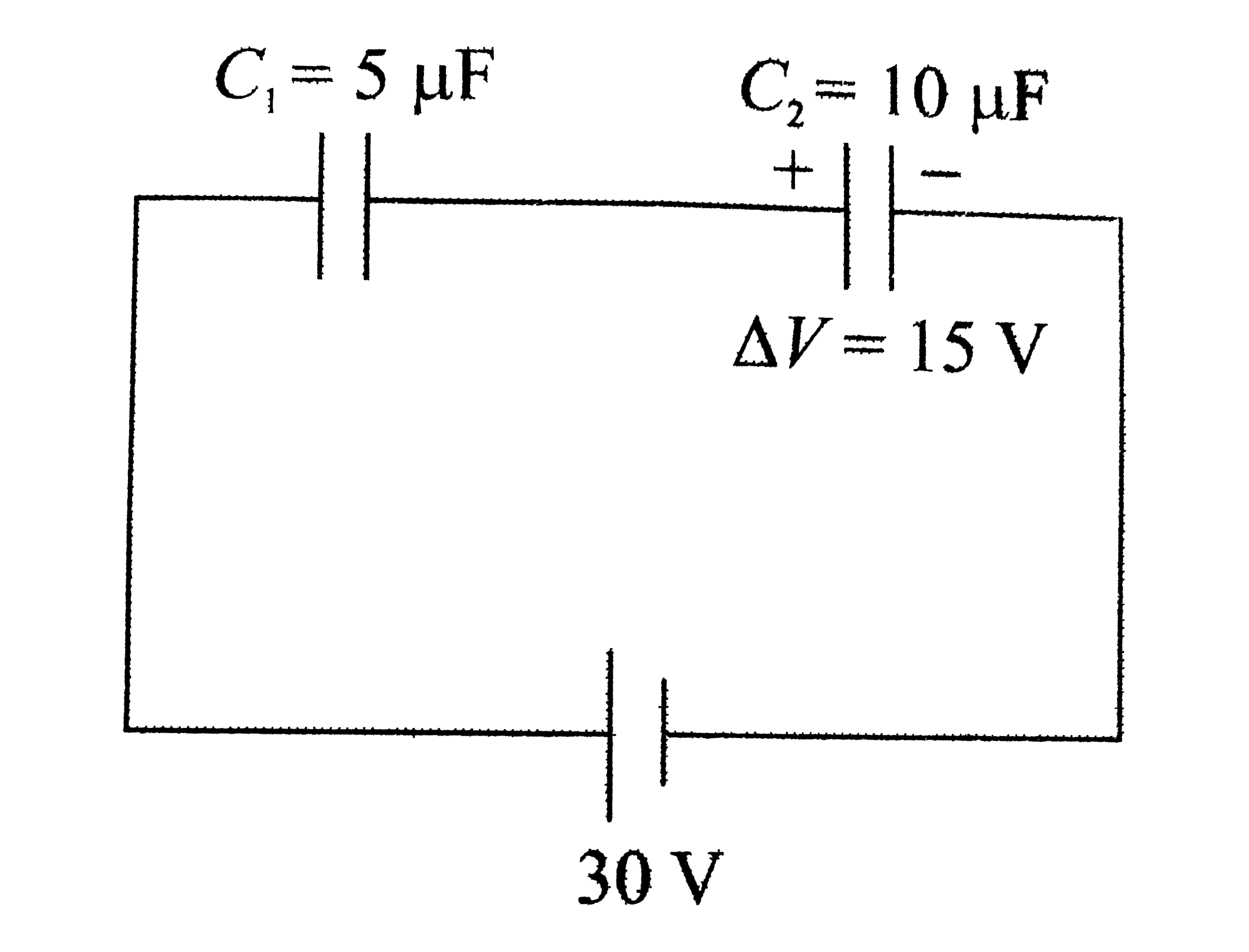
View SolutionA capacitor is charged to a potential of V0. It is connected with an inductor through a switch S. The switch is closed at time t=0. Which of the following statement(s) is/are correct?

View SolutionA 16 μF capacitor is charged to a 20 Volt potential. Battery is then disconnected and inductor of inductance 40mH is connected across the capacitor, So that LC oscillations are step-up. Maximum current in the coil is
View SolutionA capacitor is connected to a 12 V battery through a resistance of (10Ω).It is found that the potential difference across the capacitor rises to 4.0 V in 1(mu)s. find the capacitance of the capacitor.
View Solution
