A coil carrying a steady current is short-circuited. The current in it decreases α times in time t0. The time constant of the circuit is
τ=t0 In α
τ=t0Inα
τ=t0α
τ=t0α−1
The correct Answer is:B
To solve the problem, we need to find the time constant τ of a coil that is short-circuited, causing the current to decrease by a factor of α in a time t0.
1. Understanding the Problem:
- We have a coil with an initial current I0.
- When the coil is short-circuited, the current decreases to I0α in time t0.
2. Using the Exponential Decay Formula:
- The current in an inductor decays according to the formula:
I(t)=I0e−tτ
- At t=t0, the current is:
I(t0)=I0α
3. Setting Up the Equation:
- Substitute t=t0 into the exponential decay formula:
I0α=I0e−t0τ
4. Canceling I0:
- Since I0 is not zero, we can divide both sides by I0:
1α=e−t0τ
5. Taking the Natural Logarithm:
- To solve for τ, take the natural logarithm of both sides:
ln(1α)=−t0τ
- This can be rewritten using the property of logarithms:
−ln(α)=−t0τ
6. Rearranging the Equation:
- Multiply both sides by -1:
ln(α)=t0τ
- Rearranging gives:
τ=t0ln(α)
7. Final Result:
- The time constant τ of the circuit is:
τ=t0ln(α)
Conclusion:
- The correct answer is option 2: τ=t0ln(α).
- We have a coil with an initial current I0.
- When the coil is short-circuited, the current decreases to I0α in time t0.
- The current in an inductor decays according to the formula:
I(t)=I0e−tτ
- At t=t0, the current is:
I(t0)=I0α
- Substitute t=t0 into the exponential decay formula:
I0α=I0e−t0τ
- Since I0 is not zero, we can divide both sides by I0:
1α=e−t0τ
- To solve for τ, take the natural logarithm of both sides:
ln(1α)=−t0τ
- This can be rewritten using the property of logarithms:
−ln(α)=−t0τ
- Multiply both sides by -1:
ln(α)=t0τ
- Rearranging gives:
τ=t0ln(α)
- The time constant τ of the circuit is:
τ=t0ln(α)
- The correct answer is option 2: τ=t0ln(α).
Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (multiple Correct )
7 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (assertion-reasoning)
2 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (subjective)
7 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
Similar Questions
The time constant of the circuit shown is :

View SolutionThe time constant of C-R circuit is
View SolutionConsider the circuit shown below. When switch S1 is closed, let I be the current at time t, then applying Kirchhoff's law
E−iR−Ldidt=0or∫i0diE−iR=1L∫10dt
i=ER(1−e−Rl⋅t)
LR = time constant of circuit
When current reaches its steady value (=i0, open S1 and close S2, the current does reach to zero finally but decays expnentially. The decay equation is given as i=i0e−RL⋅T).
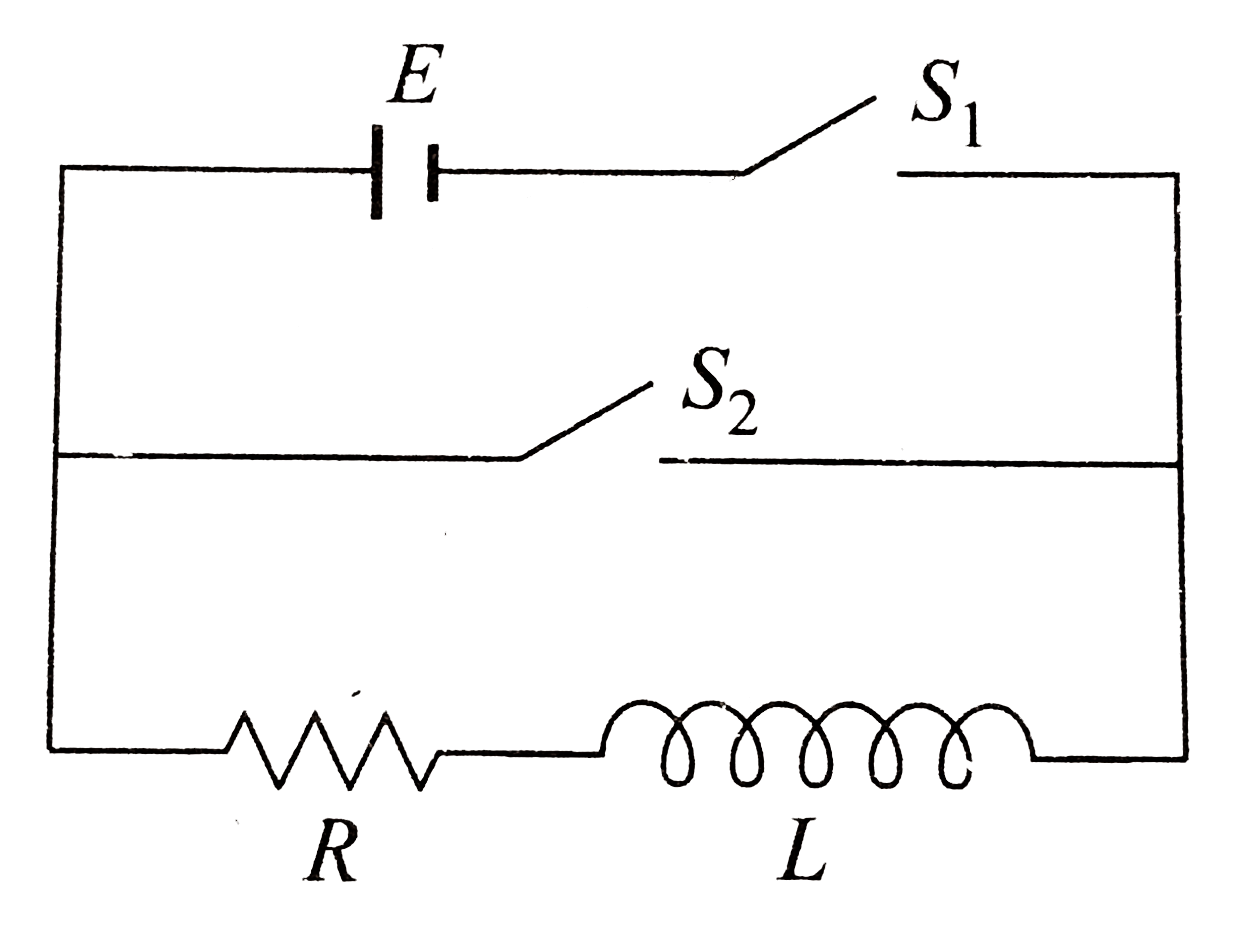
When a coil carrying a steady current is short circuited, the current decreases in it η times in time t0. The time constant of the circuit is
View SolutionTime constant of LR circuit will be
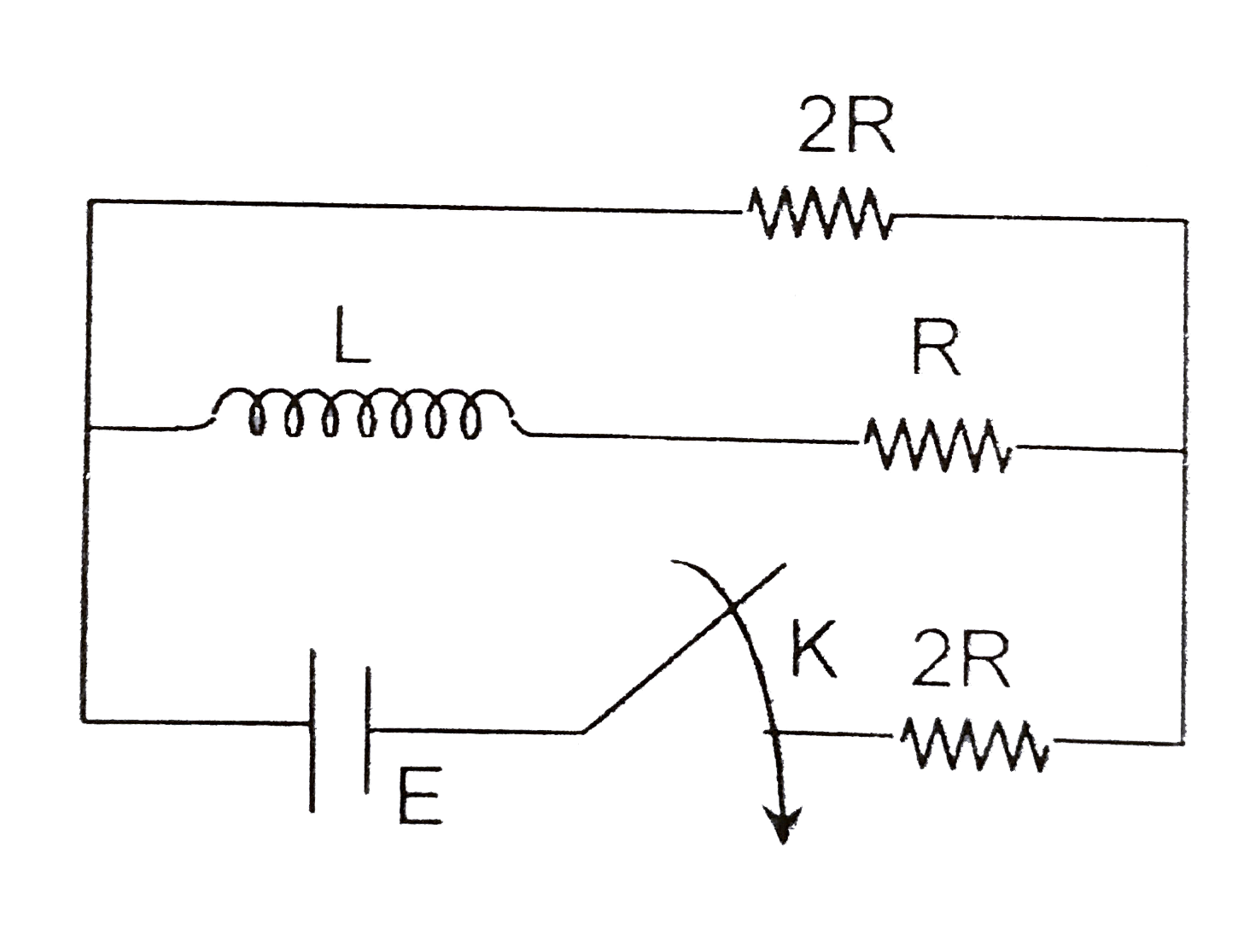
View SolutionWhen a choke coil carrying a steady current is short circuited, the current in it decreases to β(<1) times its initial value in a time T. The time constant of the choke coil is
View SolutionIn the transient circuit shown, the time constant of the circuit is :
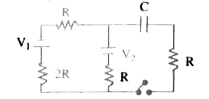
View SolutionThe value of time constant for the given circuit is
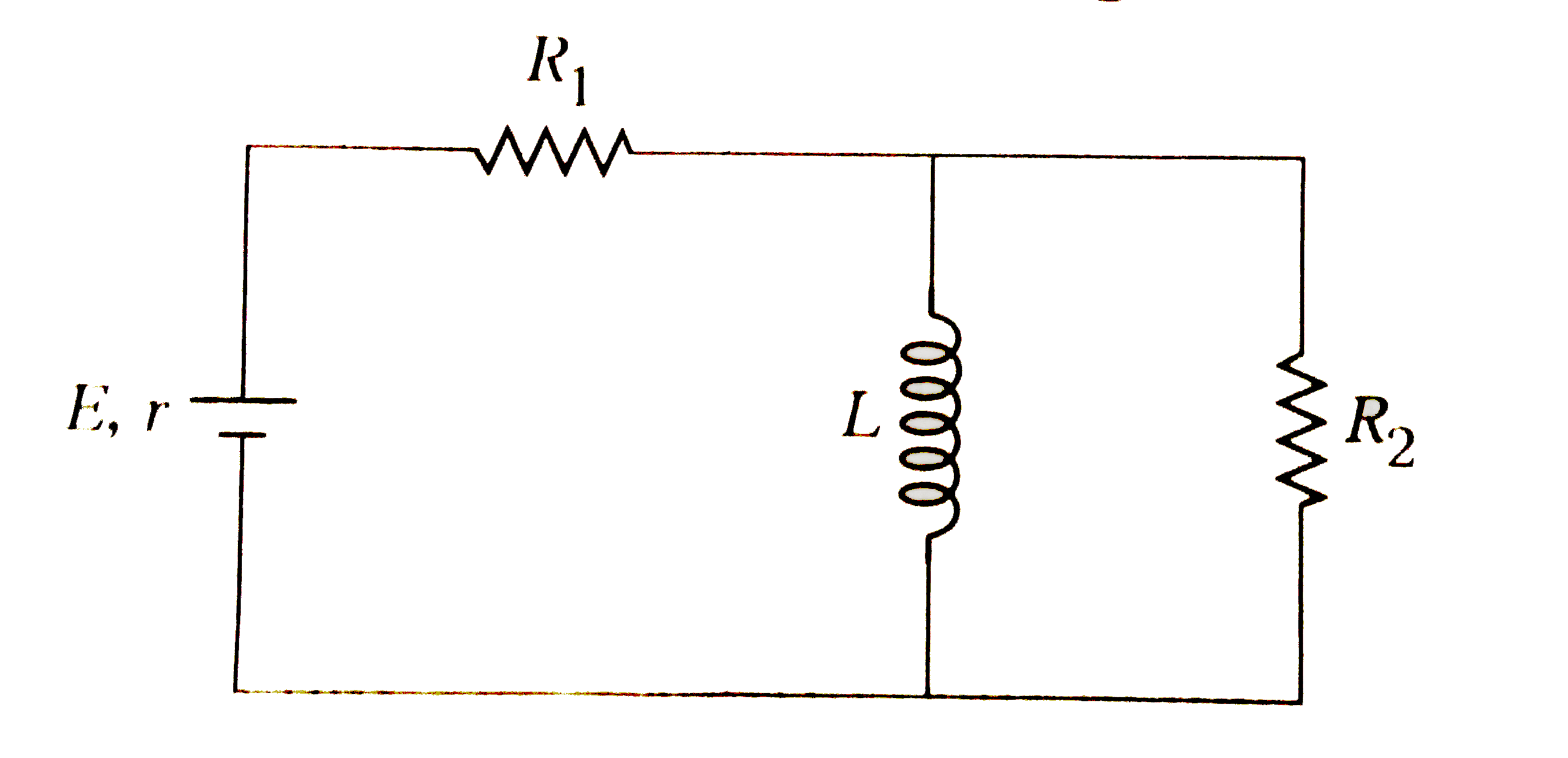
View SolutionThe time constant of the circuit shown in the figure is
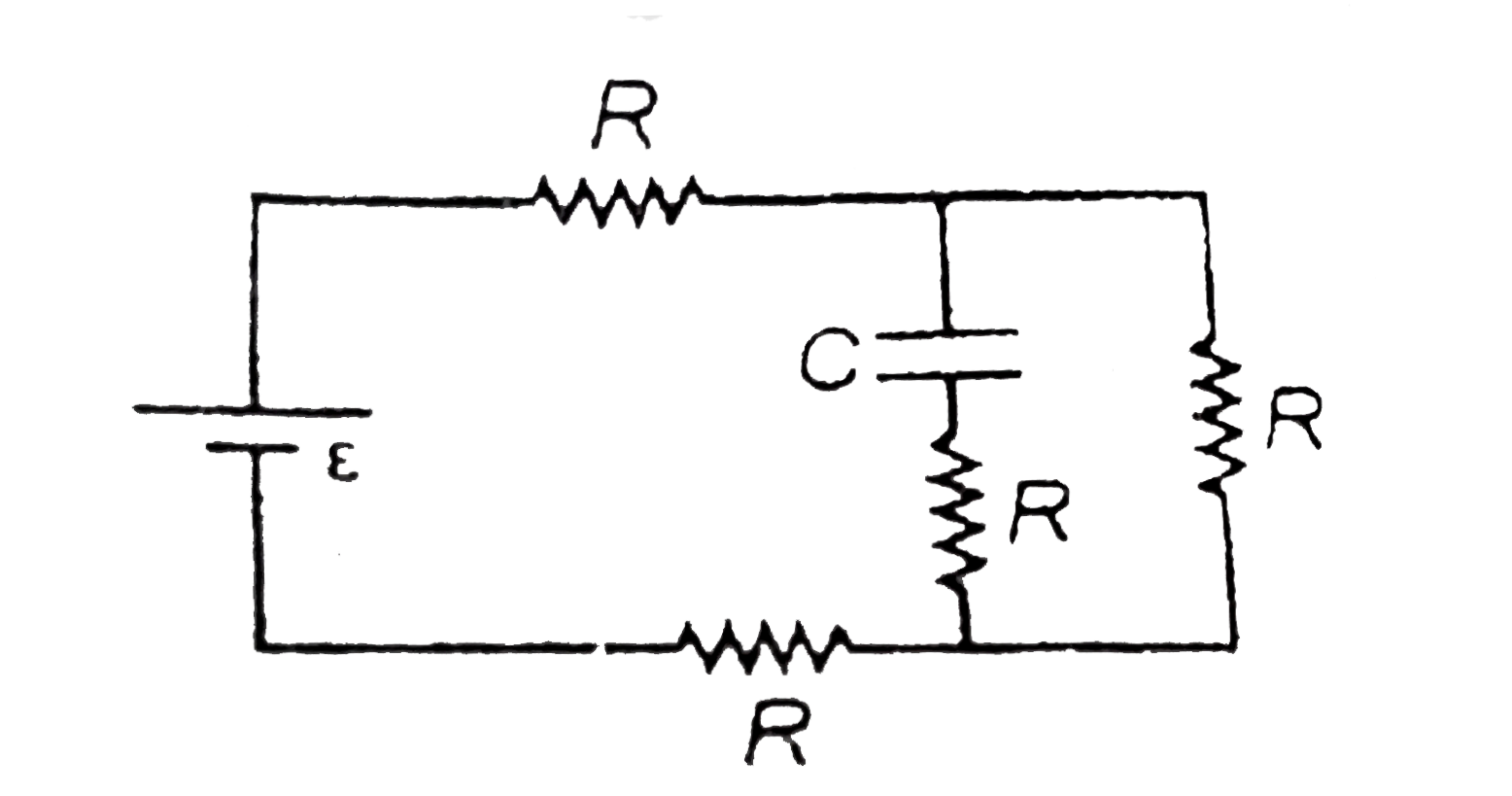
View SolutionIn an LR circuit, current at t=0 is 20A . After 2s it reduced to 18A. The time constant of the circuit is (in second)
View SolutionThe current in an L−R circuit builds upto 3/4th of its steady state value in 4sec. Then the time constant of this circuit is
View Solution
