The coefficient of static friction between a block of mass m and an incline is $μ_{s} = 03$ , a. What can be the maximum angle $θ$ of the incline with the horizontal so that the block does not slip on the plane? b. If the incline makes an angle $\frac{θ}{2}$ with the horizontal, find the frictional force on the block.

Video Solution

Text Solution

Verified by Experts

The situation is shown in ure.
a. the forces on the block are
the weight mg downwasrd by the earth
the normal contact force N by the incline, and
the friction f paralel to the incline up the plane, by the incline

As the block is ast rest, these fores should add up to zero. Also, since $θ$ is the maximum angle to prevent slipping, this is acase oflimiting equilibrium and so $f = μ_{s} N$ .
Taking components perpendicular to the incline
$N - m g cos θ = 0$
or, $N = m g cos θ$ ..............i
Taking components parallel to the incline
$f - m g sin θ = 0$
or $μ_{s} N = m g sin θ$ ..........ii ltbr> Dividing ii by i $μ_{2} = tan θ$
or, $θ = {tan}^{- 1} μ_{s} = {tan}^{- 1} (0.3)$
b. If the angle of incline is reduced to $\frac{θ}{2}$ the equilibrium is not limiting and hence the force of static friction f is less than $μ_{s} N$ . To know the value of f we proceed as in part a. get the equations
$N = m g cos (\frac{θ}{2})$
and $f = m g sin (\frac{θ}{2})$
Thus, the force of friction is $m g sin (\frac{θ}{2})$ .

Updated on:21/07/2023

Class 11 PHYSICS FRICTION

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
A solid cylinder of mass $m$ rolls without slipping down an inclined plane making an angle $θ$ with the horizontal. The frictional force between the cylinder and the incline is
A $m g sin θ$
B $\frac{m g sin θ}{3}$
C $m g cos θ$
D $\frac{2 m g sin θ}{3}$
Question 2 - Select One
A block of mass $m$ is placed on a rough inclined plane. The coefficient of friction between the block and the plane is $μ$ and the inclination of the plane is $θ$ . Initially $t h e a t - 0$ and the block will certain stationary on the plane. Now the inclination $θ$ is gradually increased. The block presses the inclined plane with a force $m g cos θ$ . So welding strength between the block and inclined is $μ m g cos θ$ , and the pulling forces is $m g sin θ$ . As soon as the pulling force is greater than the welding strength, the welding breaks and the block starts sliding, the angle $θ$ for which the block starts sliding is called angle of repose $(λ)$ . During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction $($ frictional force $)$ and the shear reaction (frictional force) . The net contact force will be resultant of both.

If the entire system, were accelerated upward with acceleration $' a'$ , the angle of repose , would $:$
Aincreases
Bdecreases
Cremain same
Dincrease of $a > g$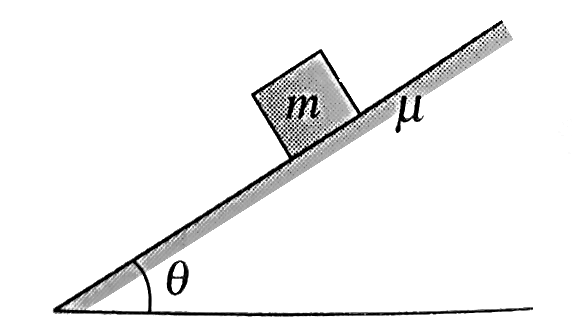
Question 3 - Select One
A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is $μ$ and the inclination of the plane is $θ$ .Initially $θ = 0$ and the block will remain stationary on the plane. Now the inclination $θ$ is gradually increased . The block presses theinclined plane with a force $m g cos θ$ . So welding strength between the block and inclined is $μ m g cos θ$ , and the pulling forces is $m g sin θ$ . As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle $θ$ for which the block start sliding is called angle of repose $(λ)$ . During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
Answer the following questions based on above comprehension:
Q. If $μ = \frac{3}{4}$ then what will be frictional force (shear force) acting between the block and inclined plane when $θ = 30^{\circ}$ :
A $\frac{3 \sqrt{3}}{8} m g$
B $\frac{m g}{2}$
C $\frac{\sqrt{3}}{2} m g$
Dzero