The cyclontron's oscillator frequency is equlal to v=10MHz. Find the effective voltage applied across the does of that cyclotron if the distance between the neighbouring trajecroies of protons is not less than Δr=1.0cm, with the trajectory radius being equal to r=0.5m.
We know that for a charged particle (proton) in a magnetic field,
mv2r=Bev or mv=Ber
But, ω=eBm,
Thus E=12mv2=12mω2r2.
So, ΔE=mω2rΔr=4π2v2mrΔr
On the hand ΔE=2eV, where V is the effective acceleration voltage, across the Does, there being two crossings per revolution. So,
V≥2π2v2mrΔr/e
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electromagnetic Induction84videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions6videos
ELECTRICITY AND MAGNETISM
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions24videos
ELECTROMAGNETISM
Similar Questions
Singly charged ions He+ are accelerated in a cyclotron so that their maximum orbital radiys is r=60cm. The frequency of a cyclotron's oscillator is equal to v=10.0MHz, the effective accelearating volatage across the deos is V=50kV. Neglecting the gap between the does, find:
(a) the total time of acceleration of the ion,
(b) the appoximate distance covered by the ion in the process of its acceleration.View SolutionShow that the frequency intervals between the neighbouring spectral lines of a true ratational spectrim of a diatomic molecules are equal. Find the moment of intertial and the distance between the nuclei of a CH molecule if the intervals between the neighbouring lines of the true rotational spectrum of these molecules are equal to Δω=5.47.1012s−1
View Solution
Knowledge Check
- Question 1 - Select One
The oscillating frequency of a cyclotron is 10MHz. If the radius of its Dees is 0.5m, the kinetic energy of a proton which is accelerated by the cyclotron is
A10.2MeVB2.55MeVC20.4MeVD5.1MeV - Question 2 - Select One
An alternate electric field of frequency v, is applied across the dees (radius=R) of a cyclotron that is being used to accelerate protons (mass=m). The operating magnetic field (b) used in the cyclotron and the kinetic energy (K) of the proton beam, produced by it, are given by
AB=mveandK=2mπ2v2R2BB=2πmveandK=m2πvR2CB=2πmveandK=2mπ2v2R2DB=mveandK=m2πvR2
An air cylindrical capacitor eith a dc voltage V=200V applied across it is being submerged vertivally into a vessel filled with water at a velocity v=5.0mm/s. The electrodes of the capacitors are separated by a distance d=2.0mm, the mean curvature radius of the electrodes is equal to r=50mm. Find the current flowing in this case along lead wires, if d<<r.
View SolutionProtons are accelerated in a cyclotron so that the maximum curvature radius of their trajectory is equal to r=50cm. Find:
(a) the kinetic energy of the protons when the acceleration is completed if the magnetic induction in the cyclotron is B=1.0T,
(b) the minimum frequency of the cycloroton's oscillator at which the kinetic energy of the protons amounts to T=20MeV by the end of accelearation.View SolutionA cyclotron’s oscillator frequency is 10 MHz. What should be the operating magnetic field for accelerating protons, if the radius of its dees is 60 cm ? What is the kinetic energy of the proton beam produced by the accelerator? Given e=1.6×10–19C,m=1.67×10–27 kg. Express your answer in units of MeV [1MeV=1.6×10–13J].
View SolutionAn alternate electric field of frequency v, is applied across the dees (radius=R) of a cyclotron that is being used to accelerate protons (mass=m). The operating magnetic field (b) used in the cyclotron and the kinetic energy (K) of the proton beam, produced by it, are given by
View SolutionAn alternate electric field of frequency v, is applied across the dees (radius=R) of a cyclotron that is being used to accelerate protons (mass=m). The operating magnetic field (b) used in the cyclotron and the kinetic energy (K) of the proton beam, produced by it, are given by
View SolutionFind the maximum and minimum distances of the planet A from the sun S, if at a ceration moment of times it was at a distance r0 and travelling with the velocity υ0. With the angle between the radius vector and velocity vector being equal to ϕ.
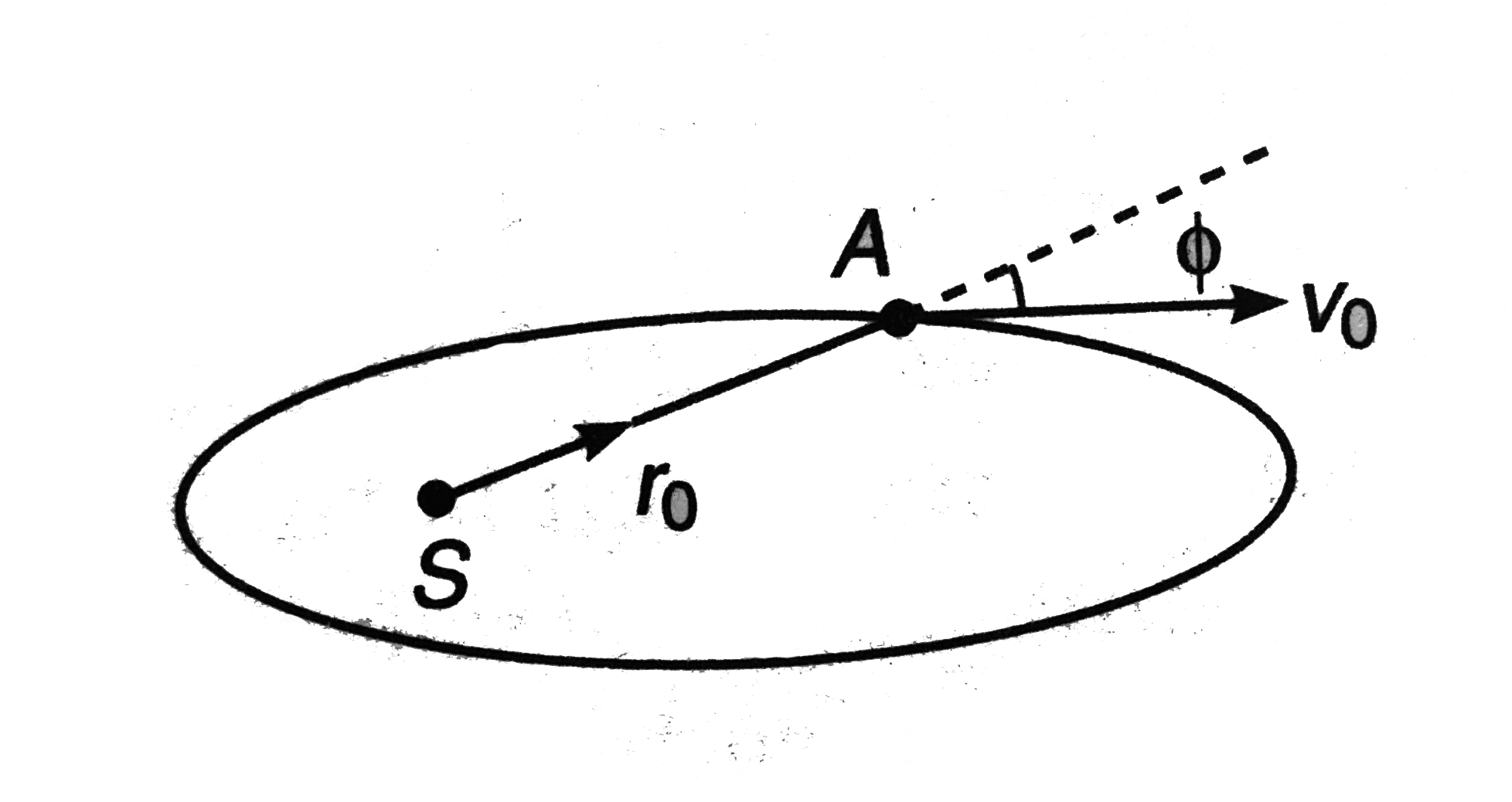 View Solution
View Solution

