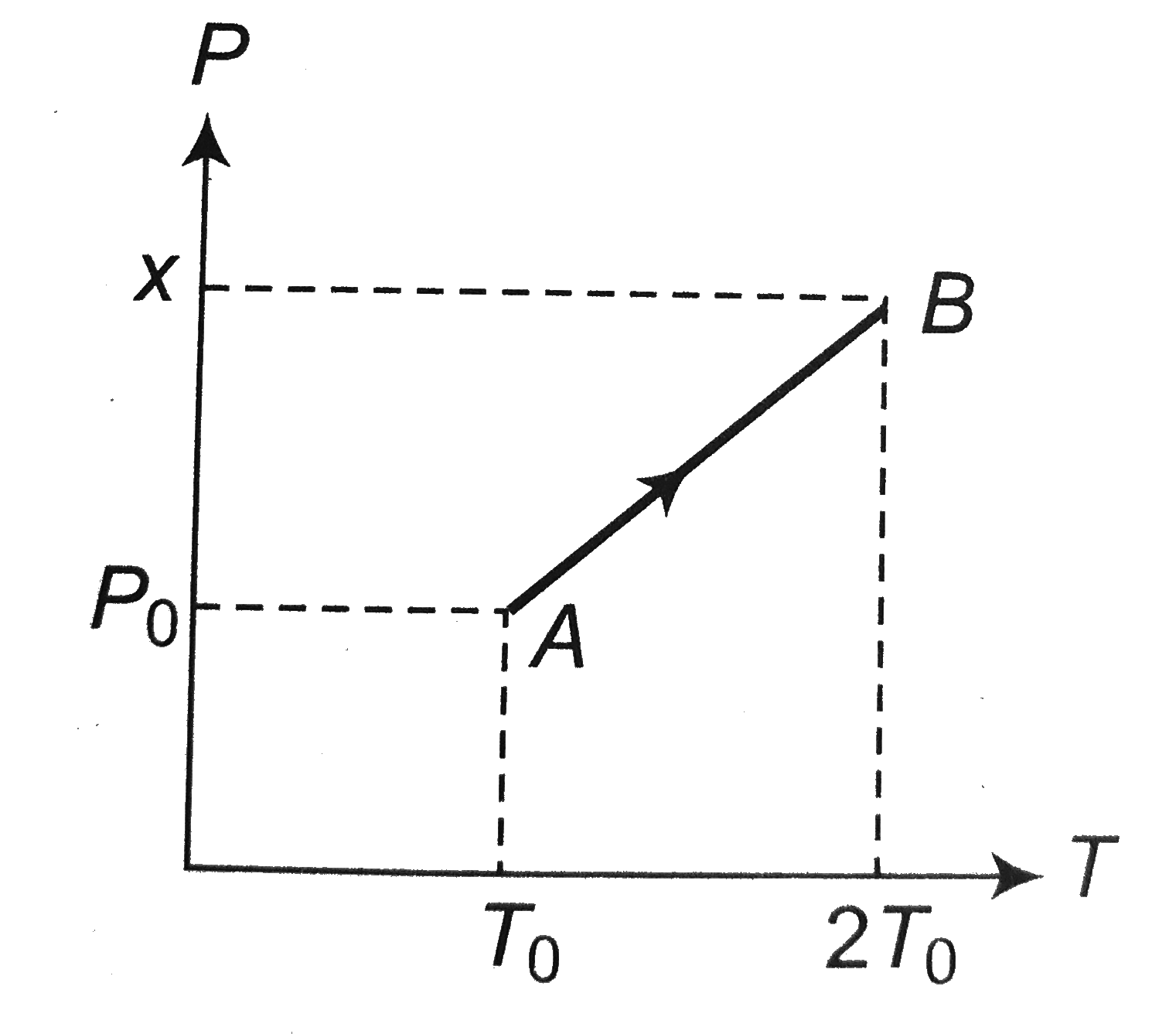
The densities at points A and B are ρ0 and 3ρ02. Find the value of x on P-axis.
2P0
32P0
3P0
4P0
The correct Answer is:C
ρ=PMRT gives ρ∝(P/T)
ρA=ρ0andρB=32ρ0
(P/T)B=32(P/T)A
(X/2T0)=(32)(P0/T0)
X=3P0.
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - A2ZCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - First Law Of Thermodynamics , Internal Energy And Work Done
55 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - A2ZCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Application Of First Law Of Thermodynamics In Different Situations
25 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - A2ZCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Chapter Test
29 Videos
- GRAVITATIONBOOK - A2ZCHAPTER - GRAVITATIONEXERCISE - Chapter Test
29 Videos
- MOCK TESTBOOK - A2ZCHAPTER - MOCK TESTEXERCISE - Motion With Constant Acceleration
15 Videos
Similar Questions
A planet is made of two materials of density ρ1 and ρ2 as shown in figure. The acceleration due to gravity at surface of planet is same as a depth 'R'. The ratio of ρ1ρ2 is x3. Find the value of x.

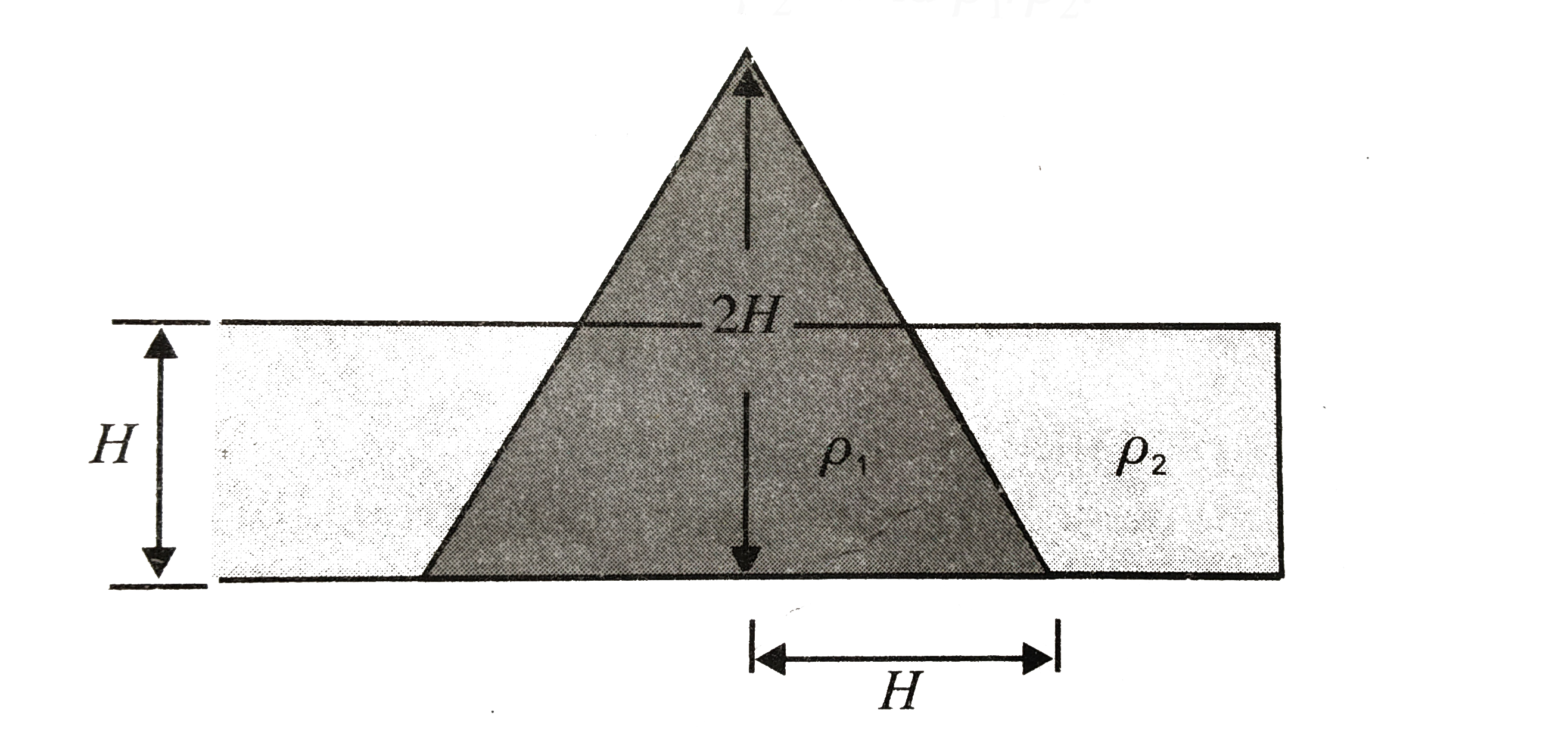
View SolutionThe light cone is in equilibrium under the action of hydrostatic forces of two liquids of densities ρ1 and ρ2. Find ρ1/ρ2. Find ρ1 and ρ2.
View Solution
Knowledge Check
Two discs have same mass and thickness. Their materials are of densities ρ1 and ρ2 . The ratio of their moment of inertia about central axis will be
Aρ1:ρ2Bρ1ρ2:1C1:ρ1ρ2Dρ2:ρ1Two circular discs A and B have equal masses and uniform thickness but have densities ρ1 and ρ2 such that ρ1>ρ2 . Their moments of inertia is
AI1>I2BI1>>I2CI1<I2DI1=I2Three liquids of densities ρ1,ρ2 and ρ3 (with ρ1>ρ2>ρ3), having the same value of surface tension T, rise to the same height in three identical capillaries. The angles of contact θ1,θ2 and θ3 obey
Aπ2<θ1<θ2<θ3<πBπ>θ1>θ2>θ3>π2Cπ2>θ1>θ2>θ3≥0D0≤θ1<θ2<θ3<π2
The earth may be regarded as a spherically shaped uniform core of density ρ1 and radius R2 surrounded by a uniform shell of thickness R2 and density ρ2. Find the ratio of ρ1ρ2 if the value of acceleration due to gravity is the same at surface as at depth R2 from the surface.
View SolutionA body of density ρ floats with volume V1 of its total volume V immersed in a liquid of density ρ1 and with the remainder of volume V2 immersed in another liquid of density ρ2 where ρ1>ρ2. Find the volume immersed in two liquids. (V1 and V2).
View SolutionA ball of radius R carries a positive charges whose volume density at a point is given as ρ=ρ0(1−r/R), Where ρ0 is a constant and r is the distance of the point from the center. Assume the permittivies of the ball and the enviroment to be equal to unity.
(a) Find the magnitude of the electric field strength as a function of hte distance r both inside and outside the ball.
(b) Find the maximum intensity Emax and the corresponding distance rm.
View SolutionA thin rod AB of length a has variable mass per unit length ρ0(1+xa) where x is the distance measured from A and ρ0 is a constant.
Find minimum value of impulse P if B passes through a point vertically above A.
View SolutionThree liquids of densities ρ1,ρ2 and ρ3 (with ρ1>ρ2>ρ3), having the same value of surface tension T, rise to the same height in three identical capillaries. The angles of contact θ1,θ2 and θ3 obey
View Solution
