The density of a rod continuously increases from to . It is easier to set it into rotation by
clamping the rod at and applying a force at , perpendicular to the rod
clamping the rod at and applying a force at , perpendicular to the rod
clamping the rod at mid point of and applying a force at , perpendicular to the rod
clamping the rod at mid-point of and applying force at , perpendicular to the rod.
The correct Answer is:B
To solve the problem of determining where it is easier to set a rod with continuously increasing density into rotation, we can follow these steps:
Step 1: Understand the Problem
The rod has a density that increases from point A to point B. We need to find out how to apply a force to make it easier to rotate the rod.
Hint: Visualize the rod and the density distribution along its length.
Step 2: Identify the Center of Mass
Since the density increases from A to B, the center of mass of the rod will be closer to point B. This is because the mass distribution is not uniform; more mass is concentrated towards B.
Hint: Remember that the center of mass is affected by the distribution of mass along the length of the rod.
Step 3: Understand Torque and Moment of Inertia
To rotate an object, torque (τ) is applied, which is related to the moment of inertia (I) and angular acceleration (α) by the equation:
τ=I⋅α
For easier rotation, we want to maximize α, which means we need to minimize I.
Hint: Recall that moment of inertia depends on the mass distribution relative to the axis of rotation.
Step 4: Determine the Moment of Inertia
The moment of inertia of the rod about an axis depends on how far the mass is from that axis. If we pivot the rod at point B, the mass distribution (and thus the moment of inertia) will be less compared to pivoting at point A.
Hint: Consider how the distance from the axis of rotation affects the moment of inertia.
Step 5: Conclusion on Clamping Point
Since we want to minimize the moment of inertia to maximize angular acceleration, we should clamp the rod at point B and apply the force at point A. This configuration will allow for the easiest rotation of the rod.
Hint: Think about how the choice of pivot point influences the effectiveness of the applied force.
Final Answer
To set the rod into rotation more easily, clamp the rod at point B and apply a force F at point A, perpendicular to the rod.
The rod has a density that increases from point A to point B. We need to find out how to apply a force to make it easier to rotate the rod.
Since the density increases from A to B, the center of mass of the rod will be closer to point B. This is because the mass distribution is not uniform; more mass is concentrated towards B.
To rotate an object, torque (τ) is applied, which is related to the moment of inertia (I) and angular acceleration (α) by the equation:
τ=I⋅α
For easier rotation, we want to maximize α, which means we need to minimize I.
The moment of inertia of the rod about an axis depends on how far the mass is from that axis. If we pivot the rod at point B, the mass distribution (and thus the moment of inertia) will be less compared to pivoting at point A.
Since we want to minimize the moment of inertia to maximize angular acceleration, we should clamp the rod at point B and apply the force at point A. This configuration will allow for the easiest rotation of the rod.
To set the rod into rotation more easily, clamp the rod at point B and apply a force F at point A, perpendicular to the rod.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Linked Comprehension
28 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective
13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
Knowledge Check
The moment of inertia of a rod about its perpendicular bisector is I . When the temperature of the rod is increased by ΔT , the increase in the moment of inertia of the rod about the same axis is (Here , α is the coefficient of linear expansion of the rod )
AαIΔTB2αIΔTCαIΔT2D2IΔTα
The kinetic energy of a particle continuously increases with time
View SolutionEntropy of universe is continuously increasing.
View Solutionin which fo the following cases the centre of mass of a rod is certainly not at its centre?
(A) The density continuously increases from left ot right
(B) The density continuously decreases from left to right
(C) The density decreases from left to right up to the centre and then increases
(D) The density increases from left to right up to the centre and then decreases
Select correct alternative.
View SolutionThe density of a rod AB increases linearly from A to B its midpoint is O and its centre of mass is at C. four axes pass through A, B, O and C, all perpendicular to the length of the rod. The moment of inertial of the rod about these axes are IA,IB,IO and IC respectively.
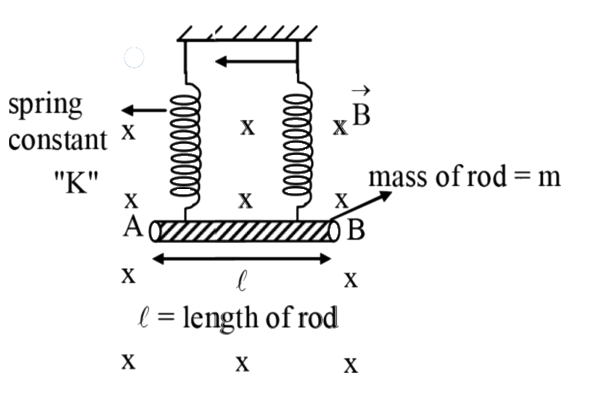
View SolutionIf the extension in both the springs increases from x to x0 on flowing current i in the rod from B to A then, the value of magnetic field will be -
View SolutionDensity of population increases when________.
View SolutionThe density of a rod of length L varies as ρ=A+Bx where x is the distance from the left end. Locate the centre of mass.

View Solution
