The displacement of a body along X-axis depends on time as √x=t+1. Then the velocity of body.
increases with time
decreases with time
independent of time
None of these
The correct Answer is:A
To solve the problem, we need to find the velocity of a body whose displacement along the X-axis is given by the equation √x=t+1.
Step 1: Rearranging the equation
We start with the given equation:
√x=t+1
To eliminate the square root, we square both sides:
x=(t+1)2
Step 2: Expanding the equation
Now we expand the right-hand side:
x=t2+2t+1
Step 3: Finding the velocity
The velocity v is defined as the derivative of displacement x with respect to time t:
v=dxdt
We differentiate x=t2+2t+1:
dxdt=ddt(t2+2t+1)
Using the power rule of differentiation:
dxdt=2t+2
Step 4: Analyzing the velocity
The expression for velocity we found is:
v=2t+2
This shows that as time t increases, the velocity v also increases since it is a linear function of t.
Conclusion
Thus, the velocity of the body increases with time.
We start with the given equation:
√x=t+1
To eliminate the square root, we square both sides:
x=(t+1)2
Now we expand the right-hand side:
x=t2+2t+1
The velocity v is defined as the derivative of displacement x with respect to time t:
v=dxdt
We differentiate x=t2+2t+1:
dxdt=ddt(t2+2t+1)
Using the power rule of differentiation:
dxdt=2t+2
The expression for velocity we found is:
v=2t+2
This shows that as time t increases, the velocity v also increases since it is a linear function of t.
Thus, the velocity of the body increases with time.
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (B) Meical entrance special format questions (Assertion and reason)
19 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (B) Meical entrance special format questions (Mathch the columns)
6 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.7
15 Videos
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Medical entrances gallery
19 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
Similar Questions
If the displacement of a particle varies with time as √x=t+3
View SolutionThe displacement of a particle along the x-axis is given by x=3+8t+7t2. Obtain its velocity and acceleration at t=2s.
View SolutionThe position of a body moving along x-axis at time t is given by x=(t2−4t+6)m. The velocity of the body at time t = 3s is
View SolutionThe displacement of a body from a reference point is given by √x=2t−3, where 'x' is in metres and it is non negative number, t in seconds. This shows that the body :
View SolutionThe displacement of a particle moving in a straight line depends on time as x=αt3+βt2+γt+δ. The ratio of initial acceleration to its initial velocity depends
View SolutionThe displacement of a particle along the x-axis is given by x=asin2ωt. The motion of the particle corresponds to
View SolutionThe displacement x of a particle moving along x-axis at time t is given by x2=2t2+6t. The velocity at any time t is
View SolutionThe displacement of a particle along the x- axis it given by x=asin2ωt The motion of the particle corresponds to
View SolutionThe displacement-time graph of a body is shown in.
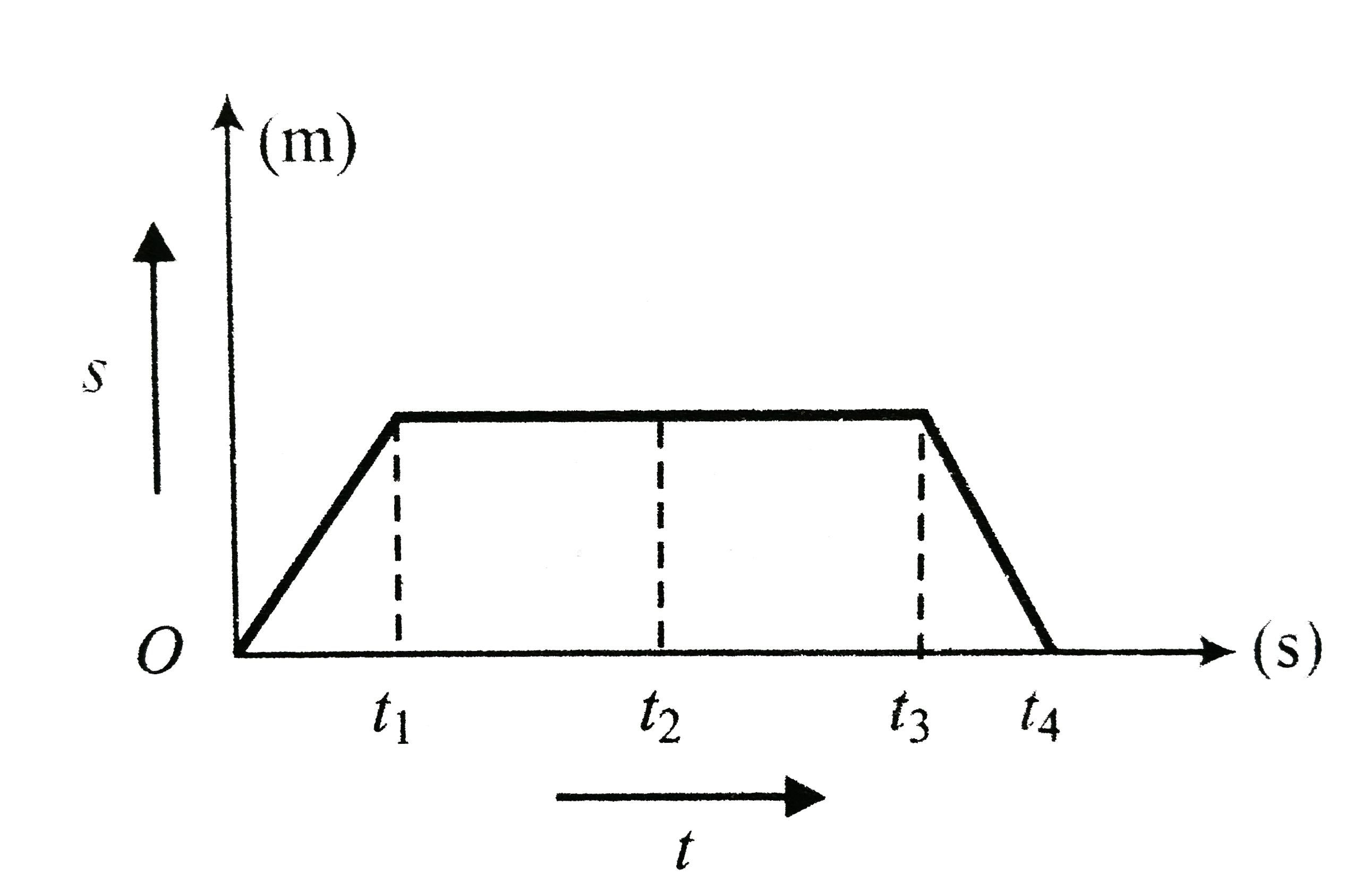 .
.
The velocity-time graph of the motion of the body will be .
View SolutionA body is projected horizontally from a point above the ground. The motion of the body
is described by the equations x = 2 t and y=5t2 where x and y are the horizontal and vertical displacements (in m) respectively at time t. What is the magnitude of the velocity of the body 0.2 second after it is projected?
View Solution
