A boggy of uniformly moving train is suddenly detached from train and stops after covering some distance. The distance covered by the boggy and distance covered by the train in the same time has relation
Both will be equal
First will be half of second
First will be 1/4 of second
No definite ratio
The correct Answer is:B
To solve the problem, we will analyze the motion of the bogey after it detaches from the train and compare the distances covered by both the bogey and the train in the same time interval.
1. Define Variables:
- Let u be the initial velocity of the bogey at the moment it detaches from the train.
- Let ab be the retardation (negative acceleration) of the bogey after detachment.
- Let Sb be the distance covered by the bogey before it stops.
- Let St be the distance covered by the train in the same time t.
2. Equation of Motion for the Bogey:
- The final velocity Vb of the bogey when it stops is 0.
- Using the equation of motion:
V2b=u2+2abSb
- Substituting Vb=0:
0=u2+2abSb
- Rearranging gives:
Sb=−u22ab
- Since ab is negative (retardation), we can write:
Sb=u22|ab|
3. Time Taken for the Bogey to Stop:
- Using the equation V=u+at:
0=u+abt
- Rearranging gives:
t=−uab
- Since ab is negative, we can express t as:
t=u|ab|
4. Distance Covered by the Train:
- The train continues to move with the same initial velocity u.
- The distance covered by the train in time t is:
St=ut=u(u|ab|)=u2|ab|
5. Finding the Ratio of Distances:
- Now we have:
Sb=u22|ab|andSt=u2|ab|
- The ratio of the distance covered by the bogey to the distance covered by the train is:
SbSt=u22|ab|u2|ab|=12
6. Conclusion:
- Therefore, the distance covered by the bogey is half of the distance covered by the train in the same time.
- The correct option is 12 or option B.
- Let u be the initial velocity of the bogey at the moment it detaches from the train.
- Let ab be the retardation (negative acceleration) of the bogey after detachment.
- Let Sb be the distance covered by the bogey before it stops.
- Let St be the distance covered by the train in the same time t.
- The final velocity Vb of the bogey when it stops is 0.
- Using the equation of motion:
V2b=u2+2abSb
- Substituting Vb=0:
0=u2+2abSb
- Rearranging gives:
Sb=−u22ab
- Since ab is negative (retardation), we can write:
Sb=u22|ab|
- Using the equation V=u+at:
0=u+abt
- Rearranging gives:
t=−uab
- Since ab is negative, we can express t as:
t=u|ab|
- The train continues to move with the same initial velocity u.
- The distance covered by the train in time t is:
St=ut=u(u|ab|)=u2|ab|
- Now we have:
Sb=u22|ab|andSt=u2|ab|
- The ratio of the distance covered by the bogey to the distance covered by the train is:
SbSt=u22|ab|u2|ab|=12
- Therefore, the distance covered by the bogey is half of the distance covered by the train in the same time.
- The correct option is 12 or option B.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (B) Meical entrance special format questions (Assertion and reason)19videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (B) Meical entrance special format questions (Mathch the columns)6videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.715videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Medical entrances gallery19videos
MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective10videos
PROJECTILE MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
A body starts from rest and moves with a uniform acceleration. The ratio of the distance covered in the nth sec to the distance covered in n sec is
A2n−1n2B1n2−1nC2n2−1n2D2n+1n2 - Question 2 - Select One
A train accelerates from rest at a constant rate α for some time and then it retards to rest at the constant rate β. If the total distance covered by the train is s, then the velocity of the train is
A[α+β2αβ×s]1/2B[α−β2αβ×s]1/2C[αβα+β×s]1/2D[αβα−β×s]1/2
If the displacement of a particle is zero, then distance covered by it
View SolutionIf the displacement of a particle is zero, then distance covered by it
View SolutionA body starts from rest and moves with constant acceleration. The ratio of distance covered by the body in nth second to that covered in n second is.
View SolutionA moving train is stopped by applying brakes. It stops after travelling 80m. If the speed of the train is doubled and retardation remain the same, it will cover a distance-
View SolutionFor the velocity - time graph shown in figure below the distance covered by the body in last two seconds of its motion is what fraction of the total distance covered by it in all the total distance covered by it in all the seven seconds
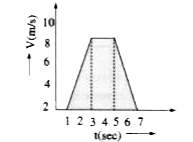 View Solution
View SolutionA stone falls freely rest. The distance covered by it in the last second is equal to the distance covered by it in the first 2 s. The time taken by the stone to reach the ground is
View Solution

