The displacement of a particle in simple harmonic motion in one time period is
A
2A
4A
zero
The correct Answer is:D
To solve the question regarding the displacement of a particle in simple harmonic motion (SHM) over one complete time period, we can follow these steps:
1. Understanding Simple Harmonic Motion (SHM):
- In SHM, a particle moves back and forth around an equilibrium position. The motion is periodic, meaning it repeats itself after a certain time interval known as the time period (T).
2. Identifying the Time Period:
- The time period (T) is the time taken for the particle to complete one full cycle of motion. In one time period, the particle will return to its starting position.
3. Analyzing the Motion:
- Let's assume the particle starts at position A (the equilibrium position). As it moves, it will reach the maximum displacement (amplitude) on one side, then return through the equilibrium position to the maximum displacement on the opposite side, and finally return to position A.
4. Determining Initial and Final Positions:
- At the start of the time period (t = 0), the particle is at position A. After one complete time period (t = T), the particle returns to position A.
5. Calculating Displacement:
- Displacement is defined as the change in position of the particle, which is the difference between the final position and the initial position.
- Since the initial position (A) and final position (A) are the same after one complete cycle, the displacement can be calculated as:
Displacement=Final Position−Initial Position=A−A=0
6. Conclusion:
- Therefore, the displacement of the particle in simple harmonic motion over one time period is zero.
Final Answer:
The displacement of a particle in simple harmonic motion in one time period is zero.
---
- In SHM, a particle moves back and forth around an equilibrium position. The motion is periodic, meaning it repeats itself after a certain time interval known as the time period (T).
- The time period (T) is the time taken for the particle to complete one full cycle of motion. In one time period, the particle will return to its starting position.
- Let's assume the particle starts at position A (the equilibrium position). As it moves, it will reach the maximum displacement (amplitude) on one side, then return through the equilibrium position to the maximum displacement on the opposite side, and finally return to position A.
- At the start of the time period (t = 0), the particle is at position A. After one complete time period (t = T), the particle returns to position A.
- Displacement is defined as the change in position of the particle, which is the difference between the final position and the initial position.
- Since the initial position (A) and final position (A) are the same after one complete cycle, the displacement can be calculated as:
Displacement=Final Position−Initial Position=A−A=0
- Therefore, the displacement of the particle in simple harmonic motion over one time period is zero.
The displacement of a particle in simple harmonic motion in one time period is zero.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:HC VERMA ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Objective-2
Explore 15 Videos
- SIMPLE HARMONIC MOTIONBook:HC VERMA ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Exercises
Explore 58 Videos
- SIMPLE HARMONIC MOTIONBook:HC VERMA ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:worked out Examples
Explore 22 Videos
- ROTATIONAL MECHANICSBook:HC VERMA ENGLISHChapter:ROTATIONAL MECHANICSExercise:Questions for short Answer
Explore 21 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBook:HC VERMA ENGLISHChapter:SOME MECHANICAL PROPERTIES OF MATTERExercise:Objective-2
Explore 7 Videos
Similar Questions
The distance moved by a particle in simple harmonic motion in one time period is
View Solution(b) The displacement of a particle executing simple harmonic motion is given by the equation y=0.3sin20π(t+0.05) , where time t is in seconds and displacement y is in meter. Calculate the values of amplitude, time period, initial phase and initial displacement of the particle.
View Solution
Knowledge Check
The displacement of a particle executing simple harmonic motion is given by y=4sin(2t+ϕ). The period of oscillation is
A2/πBπ/2CπD2πIf x, v and a denote the displacement, the velocity and the acceleration of a particle executing simple harmonic motion of time period T, then, which of the following does not change with time?
AaTvBaT+2πvCaTxDa2T+4π2v2On the basis of dimensions, decide which of the following relation for the displacement of a particle undergoing simple harmonic motion is not correct :
Ay=asin(2πtT)By=acosωtCy=aTsin(ta)Dy=a√2(sin(2πtT)+cos(2πtT))
The displacement of a particle performing simple harmonic motion is given by, x=8sinωt + 6 cos ωt, where distance is in cm and time is in second. What is the amplitude of motion?
View SolutionIf x, v and a denote the displacement, the velocity and the acceleration of a particle executing simple harmonic motion of time period T, then, which of the following does not change with time?
View SolutionOn the basis of dimensions, decide which of the following relation for the displacement of a particle undergoing simple harmonic motion is not correct :
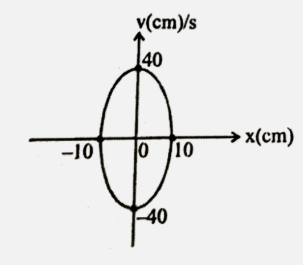
View SolutionThe plot of velocity (v) versus displacement (x) of a particle executing simple harmonic motion is shown in figure. The time period of oscillation of particle is :-
View SolutionThe phase (at a time t) of a particle in simple harmonic motion tells
View Solution