A particle executes simple harmonic motion with a frequency. (f). The frequency with which its kinetic energy oscillates is.
v2
v
2v
zero
The correct Answer is:C
To solve the problem, we need to understand the relationship between the frequency of simple harmonic motion (SHM) and the frequency of the oscillation of kinetic energy.
1. Understand the Motion: A particle executing simple harmonic motion (SHM) has a certain frequency denoted as f. This frequency is the number of complete cycles the particle completes in one second.
2. Kinetic Energy in SHM: The kinetic energy (KE) of a particle in SHM varies as the particle moves. At the mean position (the center of the motion), the particle has maximum velocity, and thus the kinetic energy is at its maximum. Conversely, at the extreme positions (maximum displacement), the velocity is zero, and so the kinetic energy is at its minimum.
3. Oscillation of Kinetic Energy: As the particle moves from one extreme position to the other, the kinetic energy goes from minimum to maximum and back to minimum. This means that one complete oscillation of kinetic energy occurs when the particle travels from one extreme to the other and back.
4. Time Period of Kinetic Energy: The time taken for the particle to go from one extreme to the other (one complete cycle of kinetic energy) is half of the time period T of the SHM. Therefore, the time period of the kinetic energy oscillation is T/2.
5. Frequency of Kinetic Energy: The frequency of an oscillation is the reciprocal of the time period. Thus, the frequency of the kinetic energy oscillation can be calculated as:
fKE=1T/2=2T
6. Relate to Frequency of SHM: The frequency of the simple harmonic motion is given by:
f=1T
Therefore, we can express the frequency of kinetic energy in terms of the frequency of SHM:
fKE=2f
7. Conclusion: The frequency with which the kinetic energy oscillates is twice the frequency of the simple harmonic motion. Thus, the correct answer is:
Frequency of kinetic energy=2×Frequency of SHM
Final Answer:
The frequency with which the kinetic energy oscillates is 2f.
---
fKE=1T/2=2T
f=1T
Therefore, we can express the frequency of kinetic energy in terms of the frequency of SHM:
fKE=2f
Frequency of kinetic energy=2×Frequency of SHM
The frequency with which the kinetic energy oscillates is 2f.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-2
15 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - worked out Examples
22 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective-2
7 Videos
Similar Questions
Knowledge Check
A particle executing simple harmonic motion with time period T. the time period with which its kinetic energy oscillates is
ATB2TC4TDT2A body of mass 20 g connected to a spring of spring constant k, executes simple harmonic motion with a frequency of (5/π) Hz. The value of spring constant is
A4Nm−1B3Nm−1C2Nm−1D5Nm−1
For a particle executing simple harmonic motion, the acceleration is -
View SolutionThe acceleration-displacement graph of a particle executing simple harmonic motion is shown in the figure. The frequency of oscillation is
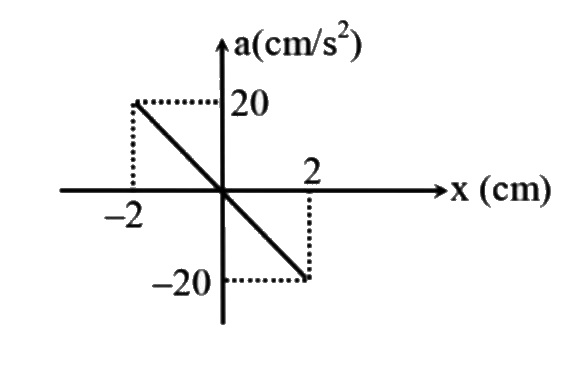
View SolutionThe acceleration-displacement (a−X) graph of a particle executing simple harmonic motion is shown in the figure. Find the frequency of oscillation.

View SolutionA particle executes SHM with frequency 4 Hz. Frequency with which its PE oscillates is
View SolutionA loaded vertical spring executes simple harmonic oscillations with period of 4 s. The difference between the kinetic energy and potential energy of this system oscillates with a period of
View SolutionA particle executes simple harmonic motion with an amplitude of 10 cm. At what distance from the mean position are the kinetic and potential energies equal?
View Solution