The displacement of a particle moving in a straight line depends on time as x=αt3+βt2+γt+δ. The ratio of initial acceleration to its initial velocity depends
The particle never returns to its starting point
The particle comes to rest after time 2α3β
The initial velocity of the particle is zero
The initial acceleration of the particle is zero
The correct Answer is:D
x= 0 at t = 0 and t=α/β. So, the particle returns to starting point at t=α/β.
υ=dxdt=2αt−3βt2
At t = 0, υ=0 i.e., initial velocity of particle is zero.
υ=0 at t = 0 and t=2α3β
Thus, the particle comes to rest after time
t=2α/3β⇒a=dυdt=2α−6βt
At t=0,a=2,a≠0
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (B) Meical entrance special format questions (Assertion and reason)19videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (B) Meical entrance special format questions (Mathch the columns)6videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.715videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Medical entrances gallery19videos
MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective10videos
PROJECTILE MOTION
Similar Questions
For a particle moving along a straight line, the displacement x depends on time t as x=αt3+βt2+γt+δ. The ratio of its initial acceleration to its initial velocity depends
View SolutionThe displacement x of a particle at time t along a straight line is given by x=α−βt+γt2. The acceleraion of the particle is
View SolutionThe displacement of a particle moving in a straight line depends on time as x=αt3+βt2+γt+δ. The ratio of initial acceleration to its initial velocity depends
View SolutionThe displacement x of a particle along a straight line at time t is given by x=a0+a1t+a2t2. The acceleration of the particle is
View SolutionA particle moves along a straight line its velocity dipends on time as v=4t−t2. Then for first 5s:
View SolutionThe acceleration-time (a−t) graph of a particle moving along straight line is as shown in figure. The time at which velocity of particle becomes equal to its initial velocity is
 View Solution
View SolutionThe displacement 'x' and time of travel 't' for a particle moving an a straight line are related as t=√(x+1)(x−1). Its acceleration at a time t is
View SolutionAt time t , the displacement of a particle moving in a straight line by x=−4t2+2t . Find the velocity and acceleration a when t = (1/2) s .
View SolutionA particle is moving in a straight line as :
a=1m/s20≤t≤10
a=2tt>10
where t is the time and a is the acceleration. If initial velocity of the particla is zero then :
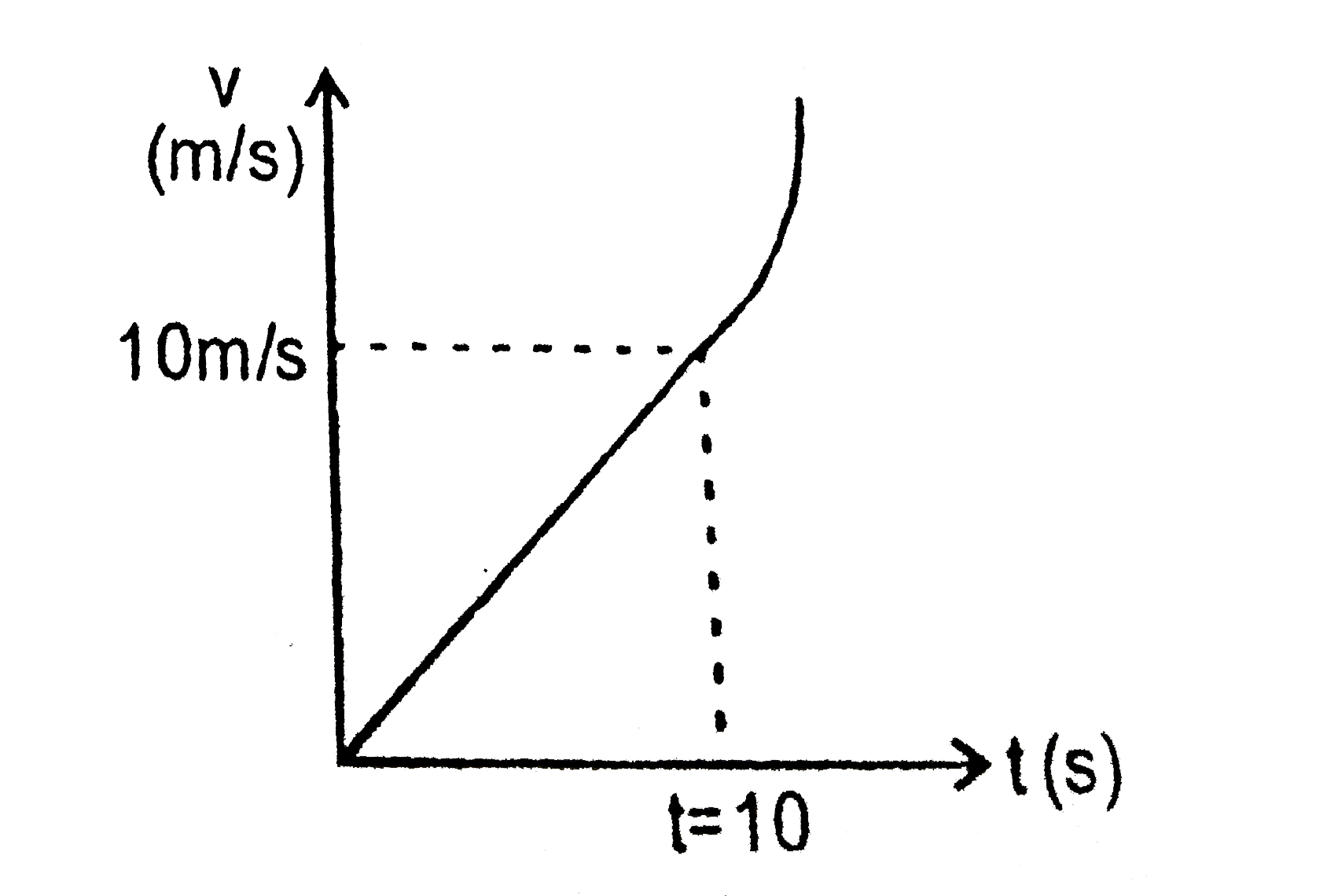 View Solution
View SolutionThe space s described in time t by a particle moving in a straight line is given by s=t5−40t3+30t2+80t−250 . Find the minimum value of acceleration.
View Solution
