The displacement x of a particle in a straight line motion is given by x=1−t−t2. The correct representation of the motion is
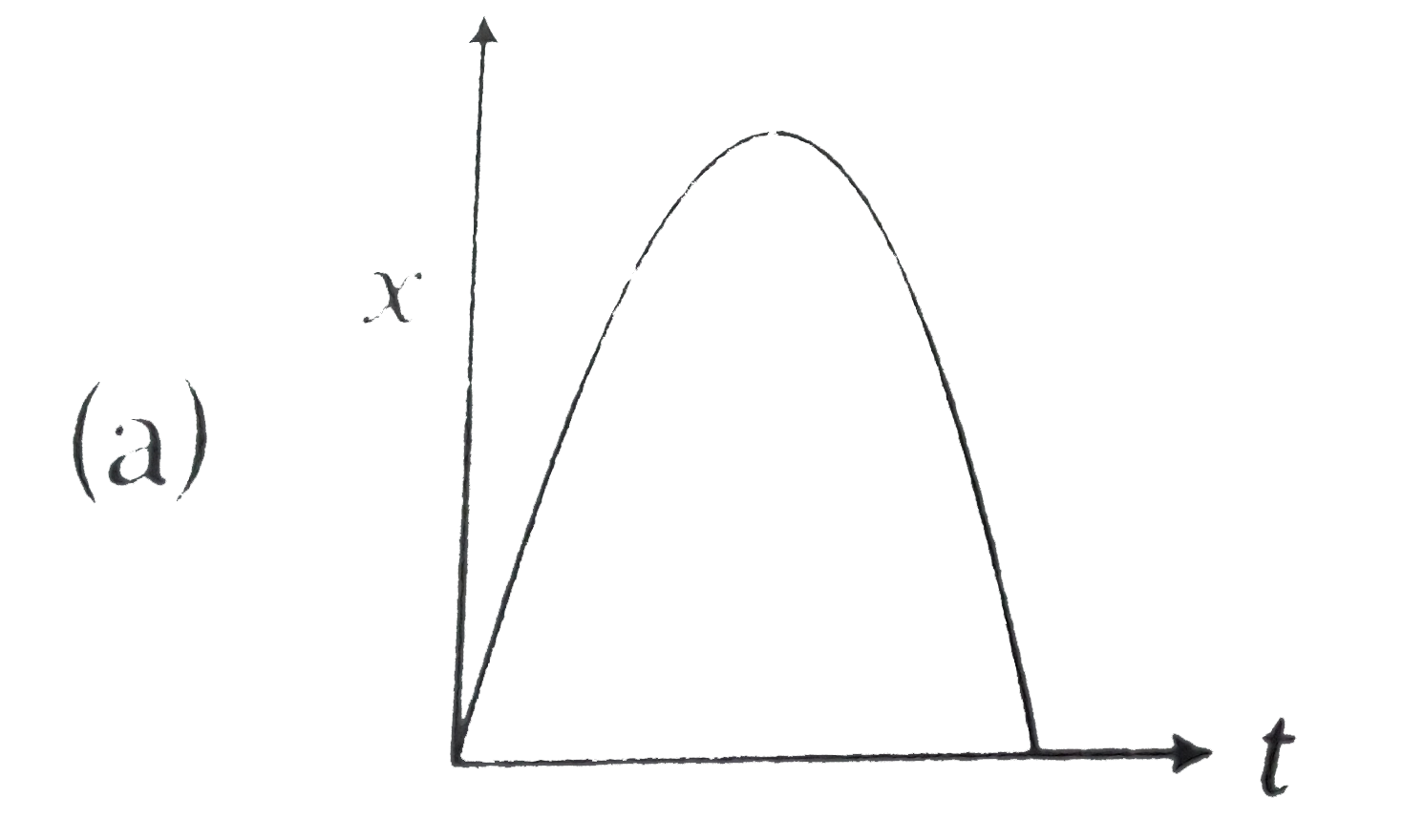
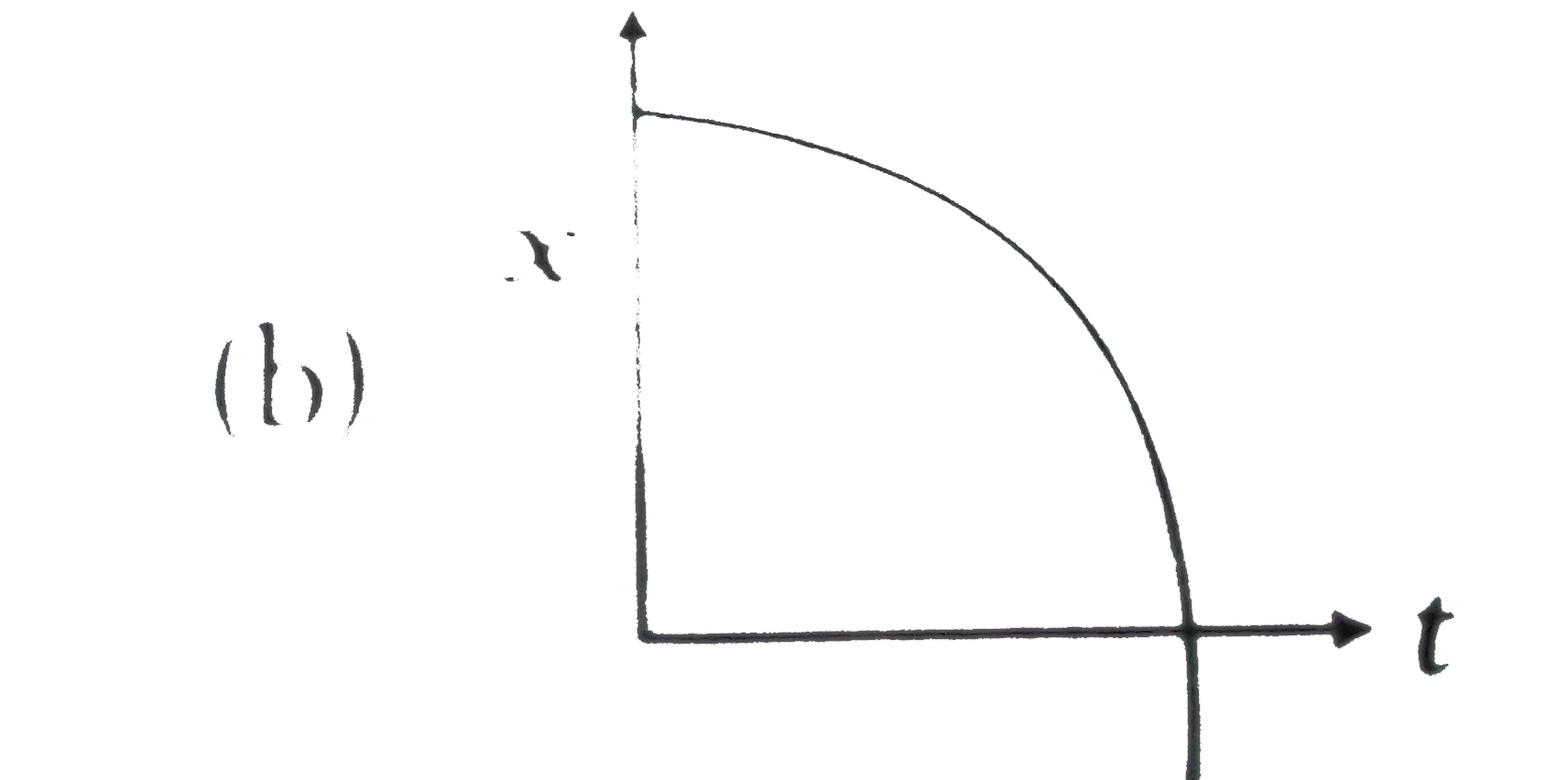
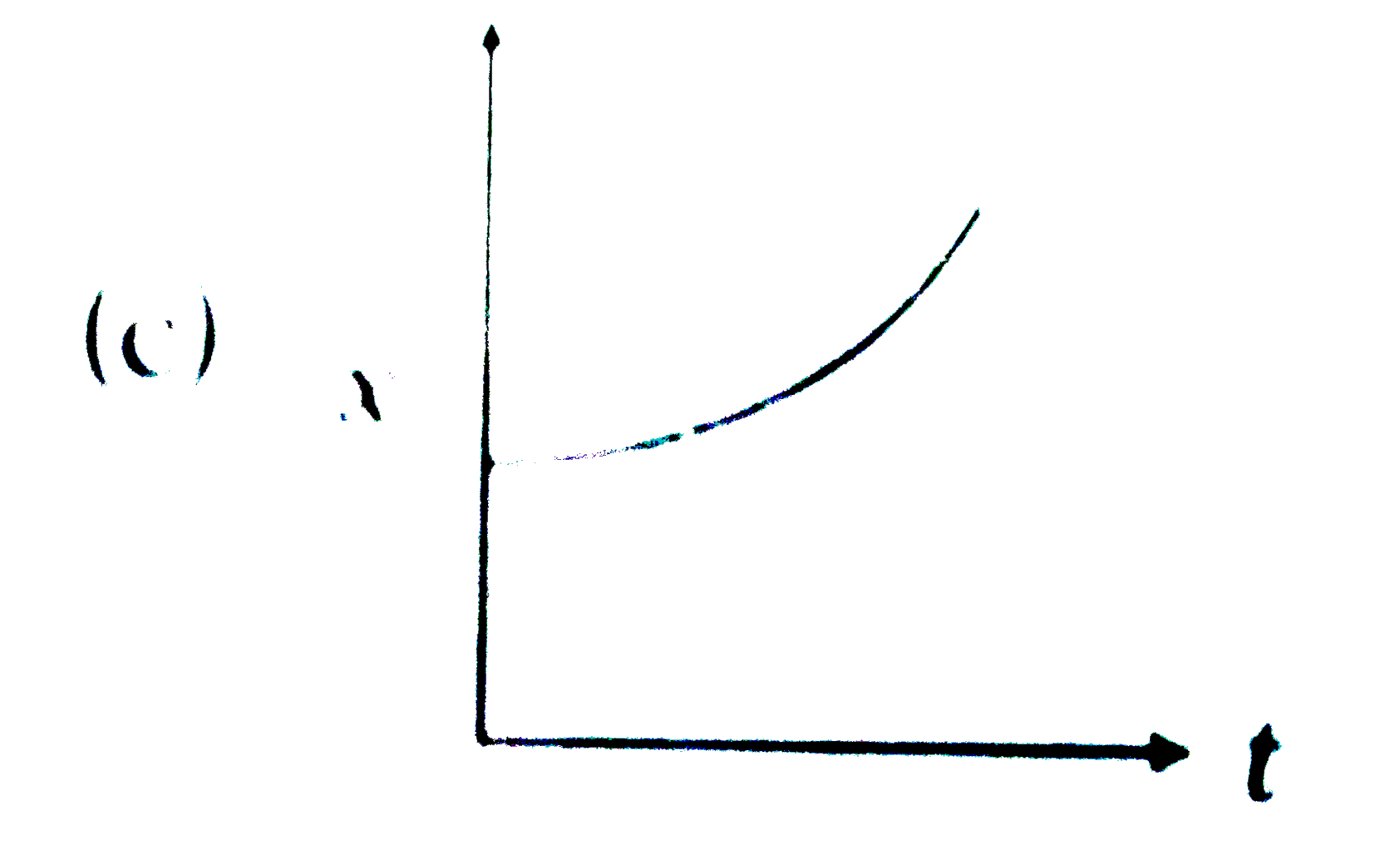
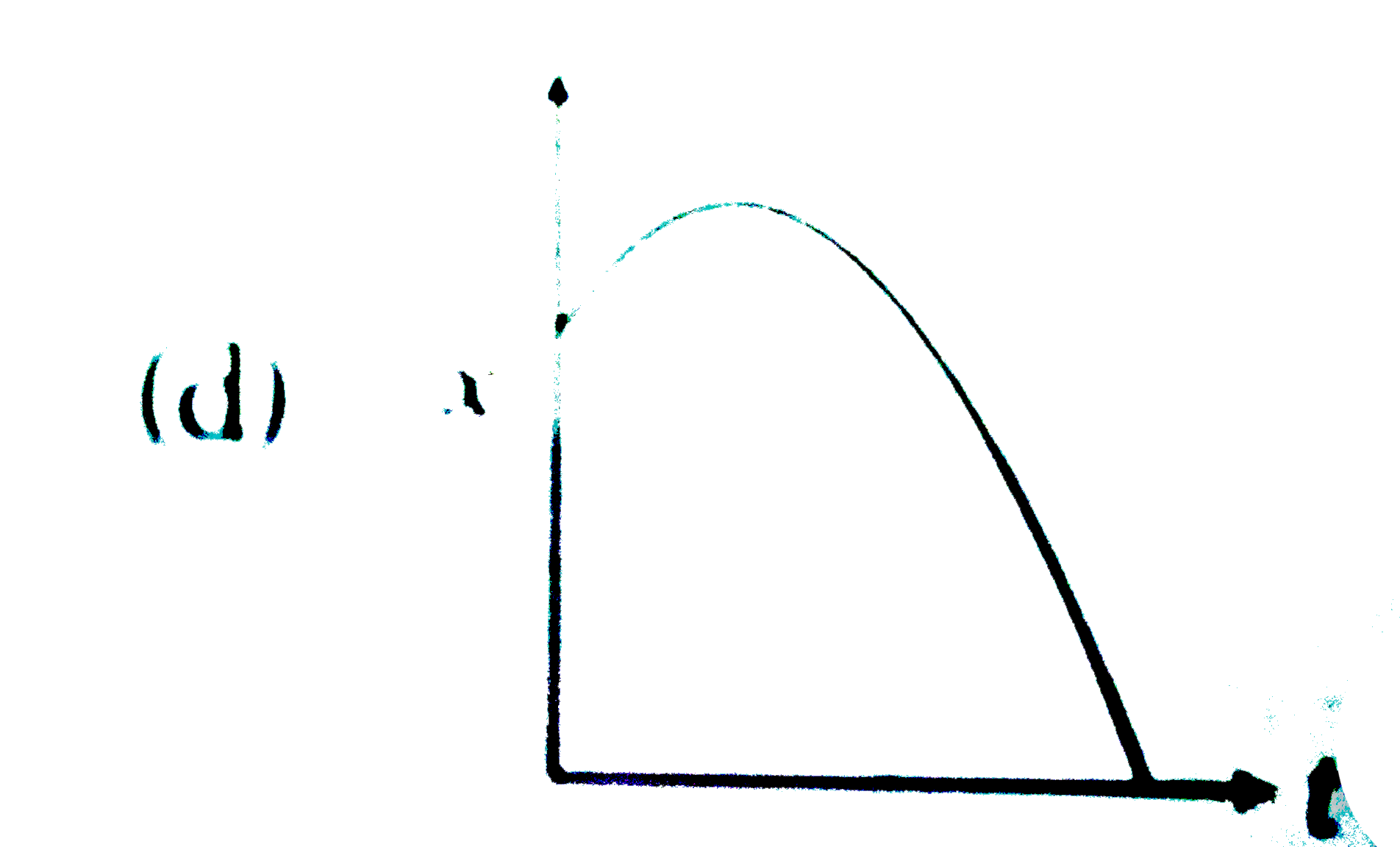
The correct Answer is:B
dxdt=υ=1−2t
Comparing with υ=u+at, we have, u=−1ms−1 and
a=−2ms−2
At t = 0, x = 1m. Then, u and a both are negative. Hence, x-coordinate of particle will go on decreasing.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (B) Meical entrance special format questions (Assertion and reason)19videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (B) Meical entrance special format questions (Mathch the columns)6videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.715videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Medical entrances gallery19videos
MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective10videos
PROJECTILE MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
The displacement of a particle executing simple harmonic motion is given by y=4sin(2t+ϕ). The period of oscillation is
A2/πBπ/2CπD2π
The motion of a particle in straight line is an example of
View SolutionThe displacement x of a particle along the x-axis at time t is given by x=a12t+a23t2. Find the acceleration of the particle.
View SolutionThe displacement (in metre) of a particle moving along X-axis is given by x=18t+5t2. The average acceleration during the interval t1=2s and t2=4s is
View SolutionAt time t , the displacement of a particle moving in a straight line by x=−4t2+2t . Find the velocity and acceleration a when t = (1/2) s .
View SolutionThe displacement (x) of a particle as a function of time (t) is given by
x=asin(bt+c)
Where a,b and c are constant of motion. Choose the correct statemetns from the following.View SolutionThe velocity-time (v-t) graph for a particle in a straight line motion is given below The corresponding accelaration-time (a-t) graph will
View SolutionThe displacement of a particle along the x-axis is given by x=asin2ωt. The motion of the particle corresponds to
View Solution
