The distance of the field point, on the equatorial plane of a small electric dipole, is halved. By what factor will the electric field, due to the dipole, change?
To solve the problem of how the electric field due to a dipole changes when the distance to the field point on the equatorial plane is halved, we can follow these steps:
1. Understand the Electric Field of a Dipole:
The electric field E at a point on the equatorial plane of a dipole is given by the formula:
E=k⋅pr3
where k is a constant (specifically 14πϵ0), p is the dipole moment, and r is the distance from the center of the dipole to the point where the electric field is being calculated.
2. Initial Distance:
Let the initial distance from the dipole to the point on the equatorial plane be r. Therefore, the electric field at this distance is:
E=k⋅pr3
3. Halve the Distance:
If the distance is halved, the new distance becomes r′=r2.
4. Calculate the New Electric Field:
Substitute r′ into the electric field formula:
E′=k⋅p(r′)3=k⋅p(r2)3
Simplifying this gives:
E′=k⋅pr38=8⋅k⋅pr3=8E
5. Conclusion:
Thus, when the distance is halved, the electric field increases by a factor of 8. Therefore, the answer to the question is:
The electric field increases by a factor of 8.
The electric field E at a point on the equatorial plane of a dipole is given by the formula:
E=k⋅pr3
where k is a constant (specifically 14πϵ0), p is the dipole moment, and r is the distance from the center of the dipole to the point where the electric field is being calculated.
Let the initial distance from the dipole to the point on the equatorial plane be r. Therefore, the electric field at this distance is:
E=k⋅pr3
If the distance is halved, the new distance becomes r′=r2.
Substitute r′ into the electric field formula:
E′=k⋅p(r′)3=k⋅p(r2)3
Simplifying this gives:
E′=k⋅pr38=8⋅k⋅pr3=8E
Thus, when the distance is halved, the electric field increases by a factor of 8. Therefore, the answer to the question is:
The electric field increases by a factor of 8.
Topper's Solved these Questions
- ELECTROSTATICS AND CURRENT ELECTRICITY BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTROSTATICS AND CURRENT ELECTRICITY EXERCISE - SHORT ANSWER QUESTIONS (2 MARKS)
59 Videos
- ELECTROSTATICS AND CURRENT ELECTRICITY BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTROSTATICS AND CURRENT ELECTRICITY EXERCISE - SHORT ANSWER QUESTIONS (3 MARKS )
23 Videos
- ELECTRONIC DEVICES BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTRONIC DEVICES EXERCISE - NUMERICALS
7 Videos
- SAMPLE QUESTION PAPER 2019BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SAMPLE QUESTION PAPER 2019EXERCISE - Section C
19 Videos
Similar Questions
Knowledge Check
The electric potential at a point on the equatorial line of a electric dipole is
Adirectly proportional to the square of the distanceBindirectly proportional to the square of the distanceCdirectly proportional to the chargeDnone of the aboveElectric field due to an electric dipole is
Aspherically symmetricBcylindrical symmetricCasymmetricDnone of the aboveElectric field due to an electric dipole is
Aspherically symmetricBcylindrical symmetricCasymmetricDnone of the above
Deive an expression for the electric field at any point on the equatorial line of an electric dipole.
View SolutionElectric potential at any point in equatorial plane of a dipole is ………. .
View SolutionFor an electric dipole, the field at a point on the equatorial line and the dipole moment are
View SolutionAssertion: The electric field due to dipole on its axis line at a distance r is E. Then electric field due to the same dipole on the equatorial line and at the same distance will be E2
Reason: Electric field due to dipole varies inversely as the square of distance.
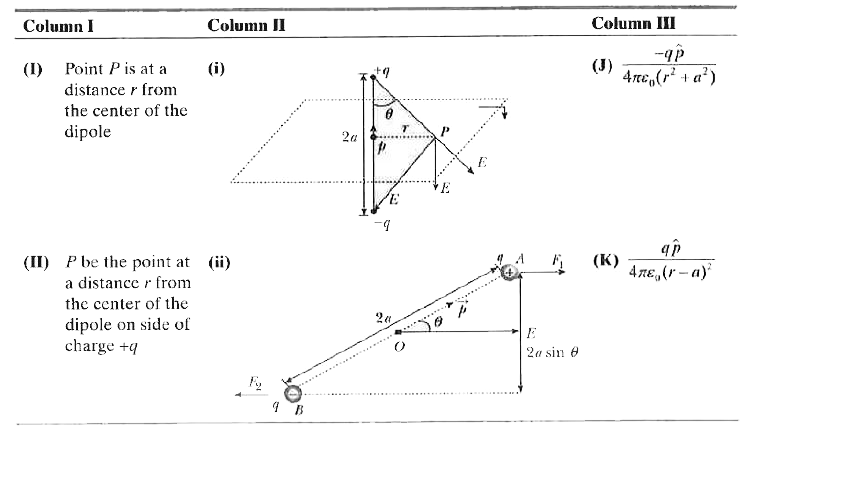
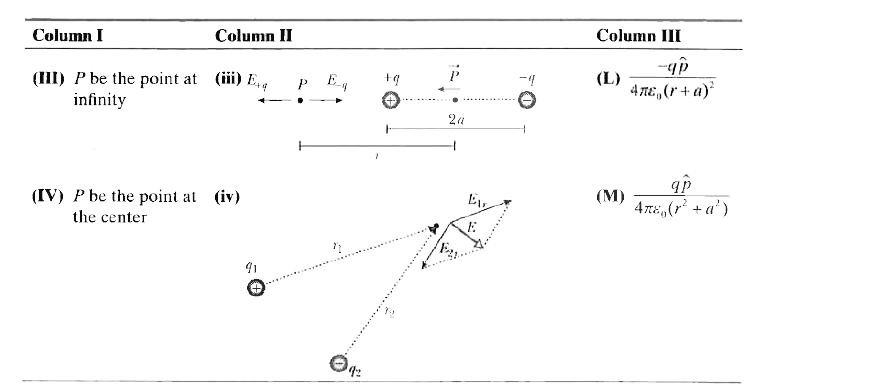
View SolutionAn electric dipole is the combination of two equal and opposite charges q and -q, respectively, separated by distance 2a. There are different points where we can find electric field due to the electric dipole. In the given table, column 1 shows different positions of point where we have to find electric field due to dipole, column 2 shows the figure of dipole with different positions of point where we have to find the electric field and column 3 shows the value or final formula of the electric field of different positions of the point.
when point P lies on the equatorial plane of the electric dipole, electric field due to +q is ?
View Solution
