Question

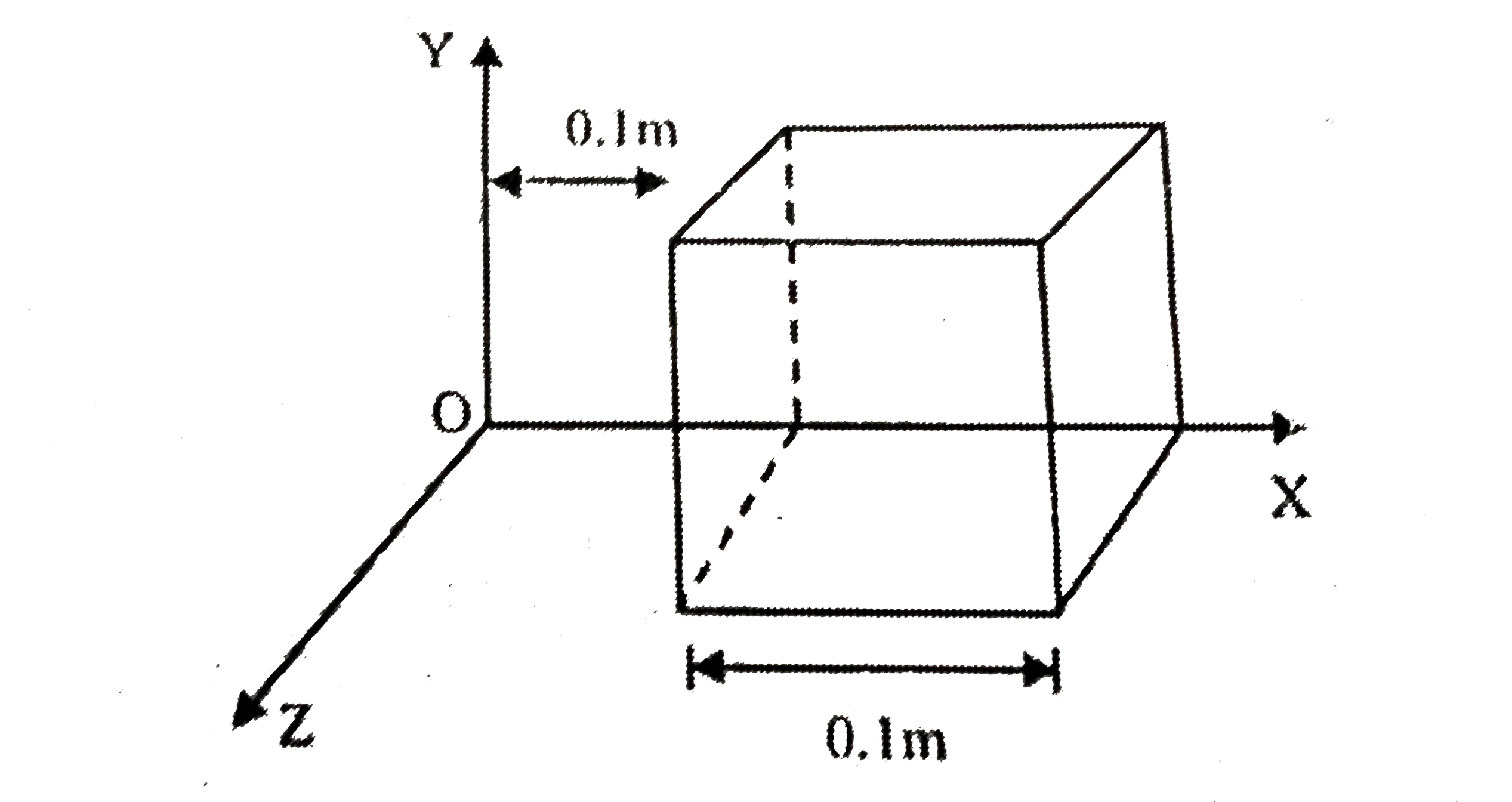
The electric field in a region is given by $\overrightarrow{E}=E_0\frac{x}{\iota }\overrightarrow{i}$. Find the charge contained inside a cubical volume bounded by the curfaced $x=0,x=\alpha ,y=0,y=\alpha ,z=0\text{and}z=\alpha$. Take $E_0=5\times {10}^{3}N{C}^{-1}$, $\iota =2cm\text{and}\alpha =1cm$.

Explanation

To find the charge contained inside the cubical volume bounded by the surfaces $$x=0,x=\alpha ,y=0,y=\alpha ,z=0,z=\alpha$$ given the electric field $$\overrightarrow{E}=\frac{E_{0}x}{\iota }\hat{i}$$, we will use Gauss's Law, which states:

$$\oint \overrightarrow{E}\cdot d\overrightarrow{A}=\frac{Q_{\text{enc}}}{{ϵ}_0}$$

Step 1: Identify the surfaces of the cube
The cube is bounded by the following surfaces:
- \( x = 0 \)
- \( x = \alpha \)
- \( y = 0 \)
- \( y = \alpha \)
- \( z = 0 \)
- \( z = \alpha \)

Step 2: Calculate the electric field at the surfaces
The electric field is given as \( \vec{E} = \frac{E_0 x}{\iota} \hat{i} \).

1. At \( x = 0 \):
\( \vec{E}(0) = \frac{E_0 \cdot 0}{\iota} \hat{i} = 0 \)

2. At \( x = \alpha \):
\( \vec{E}(\alpha) = \frac{E_0 \cdot \alpha}{\iota} \hat{i} \)

Step 3: Determine the area vectors for the surfaces
- The area vector \( d\vec{A} \) for the surface at \( x = 0 \) is directed towards the negative \( x \)-direction, so \( d\vec{A} = -dA \hat{i} \).
- The area vector \( d\vec{A} \) for the surface at \( x = \alpha \) is directed towards the positive \( x \)-direction, so \( d\vec{A} = dA \hat{i} \).

Step 4: Calculate the flux through each surface
1. For the surface at \( x = 0 \):
\( \oint \vec{E} \cdot d\vec{A} = \vec{E}(0) \cdot (-dA \hat{i}) = 0 \)

2. For the surface at \( x = \alpha \):
\( \oint \vec{E} \cdot d\vec{A} = \vec{E}(\alpha) \cdot (dA \hat{i}) = \left(\frac{E_0 \alpha}{\iota}\right) dA \)
The area \( dA \) for one face of the cube is \( \alpha^2 \) (since the cube has side length \( \alpha \)). Thus, the total flux through the surface at \( x = \alpha \) is:
\( \oint \vec{E} \cdot d\vec{A} = \left(\frac{E_0 \alpha}{\iota}\right) \alpha^2 = \frac{E_0 \alpha^3}{\iota} \)

Step 5: Apply Gauss's Law
According to Gauss's Law:
\( \frac{E_0 \alpha^3}{\iota} = \frac{Q_{\text{enc}}}{\epsilon_0} \)
Thus,
\( Q_{\text{enc}} = \epsilon_0 \frac{E_0 \alpha^3}{\iota} \)

Step 6: Substitute the values
Given:
- \( E_0 = 5 \times 10^3 \, \text{N/C} \)
- \( \iota = 2 \, \text{cm} = 0.02 \, \text{m} \)
- \( \alpha = 1 \, \text{cm} = 0.01 \, \text{m} \)
- \( \epsilon_0 = 8.854 \times 10^{-12} \, \text{C}^2/\text{N m}^2 \)

Substituting these values:
\( Q_{\text{enc}} = 8.854 \times 10^{-12} \cdot \frac{(5 \times 10^3) \cdot (0.01)^3}{0.02} \)

Calculating:
\( Q_{\text{enc}} = 8.854 \times 10^{-12} \cdot \frac{(5 \times 10^3) \cdot (1 \times 10^{-6})}{0.02} \)
\( = 8.854 \times 10^{-12} \cdot \frac{5 \times 10^{-3}}{0.02} \)
\( = 8.854 \times 10^{-12} \cdot 0.25 \times 10^{-3} \)
\( = 2.2135 \times 10^{-12} \, \text{C} \)

Final Answer
The charge contained inside the cubical volume is approximately:
\( Q_{\text{enc}} \approx 2.21 \times 10^{-12} \, \text{C} \)