The emf of a storage battery is 90V before charging and 100V after charging. When charging began the current was 10A. What is the current at the end of charging if the internal resistance of the storge battery during the whole process of charging may be taken as constant and equal to 2Ω?
To solve the problem step by step, we will follow the principles of electromotive force (emf), internal resistance, and Ohm's law.
1. Identify Given Values:
- Initial emf of the battery before charging, E1=90V
- Final emf of the battery after charging, E2=100V
- Initial current when charging began, I1=10A
- Internal resistance of the battery, r=2Ω
2. Calculate the Terminal Voltage Before Charging:
- The terminal voltage V1 when the battery is charging can be calculated using the formula:
V1=E1+I1⋅r
- Substituting the values:
V1=90V+(10A⋅2Ω)=90V+20V=110V
3. Set Up the Equation for Final Condition:
- After charging, the terminal voltage V2 is equal to the new emf E2 plus the product of the final current If and the internal resistance r:
V2=E2+If⋅r
- We know that V2 is still equal to the terminal voltage calculated before charging, which is V1=110V.
4. Substituting Known Values:
- Now we can set up the equation:
110V=100V+If⋅2Ω
5. Solve for Final Current If:
- Rearranging the equation gives:
110V−100V=If⋅2Ω
10V=If⋅2Ω
- Dividing both sides by 2Ω:
If=10V2Ω=5A
6. Conclusion:
- The final current at the end of charging is If=5A.
- Initial emf of the battery before charging, E1=90V
- Final emf of the battery after charging, E2=100V
- Initial current when charging began, I1=10A
- Internal resistance of the battery, r=2Ω
- The terminal voltage V1 when the battery is charging can be calculated using the formula:
V1=E1+I1⋅r
- Substituting the values:
V1=90V+(10A⋅2Ω)=90V+20V=110V
- After charging, the terminal voltage V2 is equal to the new emf E2 plus the product of the final current If and the internal resistance r:
V2=E2+If⋅r
- We know that V2 is still equal to the terminal voltage calculated before charging, which is V1=110V.
- Now we can set up the equation:
110V=100V+If⋅2Ω
- Rearranging the equation gives:
110V−100V=If⋅2Ω
10V=If⋅2Ω
- Dividing both sides by 2Ω:
If=10V2Ω=5A
- The final current at the end of charging is If=5A.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise 23.1
6 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise 23.2
1 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Example Type 6
1 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
Knowledge Check
The battery of a trunk has an emf of 24 V. If the internal resistance of the battery is 0.8Ω. What is the maximum current that can be drawn from the battery?
A30AB32AC33AD34A
A 50 V battery is supplying current of 10 A when connected to a resistor. If the efficiency of the battery at this current is 25%, then the internal resistance of the battery is
View SolutionA capacitor of 4μF is connected as shwon in the figure. The internal resistance of the battery is 0.5Ω. The amount of charge on the capacitor plates will be
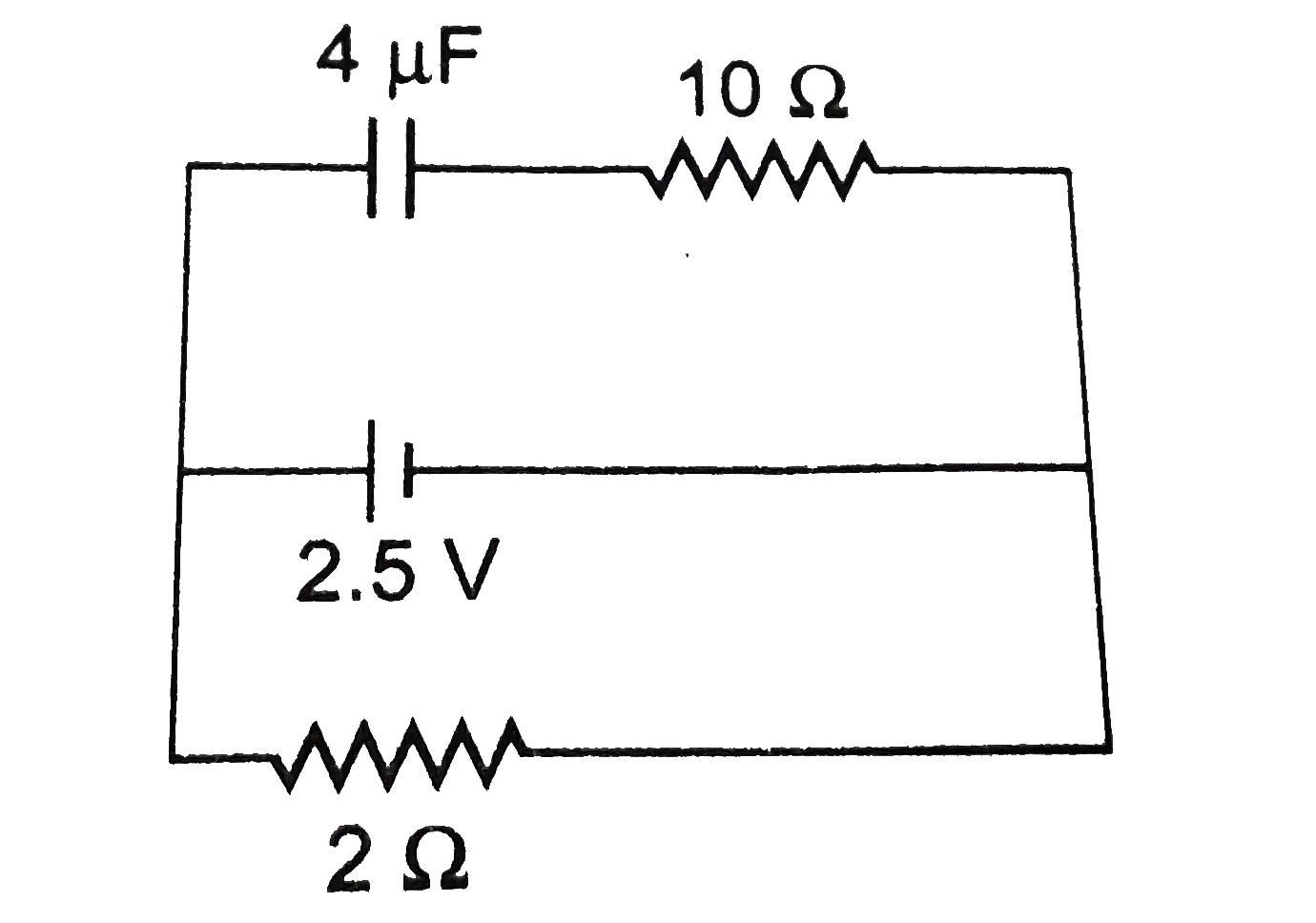
View SolutionThe potential difference between the terminals of a 6.0V battery is 7.2 V when it is being charged by a current of 2.0A.What is the internal resistance of the battery?
View SolutionThe storage battery of a car has an emf of 12 V. If the internal resistance of the battery of 0.4Ω, What is the maximum current that can be drawn from the battery ?
View SolutionA battery of emf 2.0V and internal resistance 0.10Ω is being charged with a current of 5.0A. Find the potential difference between the terminals of the battery?
View SolutionA battery of emf 10 V and internal resistance 3Ω is connected to a resistor. If the current in the circuit is 0.5 A, what is the resistance of the resistors ? What is the terminal voltage of the battery when the circuit is closed ?
View SolutionA battery of EMF E produces currents 4 A and 3 A when connected to external resistance 1Ω and 2Ω respectively. The internal resistance of the battery is
View Solution
