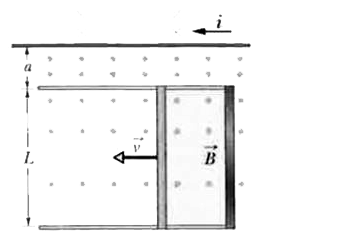
The enegry is transferred form a source of constant voltage V to a consumer by means of long straight coaxial cable with negligible active resistance. The consumed current is I. Final the enegry flux across the cross-section of the cable. The conductive sheath is supposed to be thin.
The electric field (………→) and the magnetic field (H→) are as shown. The electirc field by Gauss's therorem is like
Er=Ar
Intergrating φ=A in r2r
so A=VInr2r1(r2>r1)
Then E=VrInr2r1
Magnetic field is Hθ=I2πr
The Poynting vector S is along the Z axis and non zero between then (r1<r<r2). the total power flux is
=∫r2r1IV2πr2Inr2r1.2πrdr=Iv

Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Elastic Waves
39 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
A source of ac volatge V=V0cosωt delivers enegry yo a consummer by means of along straight coaxial cable with negligible active resistance. The current in the circuit varies as I=I0cosωt−φ. Find the time-averaged enegry flux through the cross-section of the cable. The sheath is thin.
View SolutionA long straight cable of length l is placed symmetrically along z-axis and has radius a(<<l). The cable consists of a thin wire and a co- axial conducting tube. An alternating current I(t)=I0 sin (2πvt). Flows down the central thin wire and returns along the co-axial conducting tube. the induced electric at a distance s from the wire inside the cable is
E(s,t)=μ0I0v cos (2πvt)In(sa)ˆk.
(i) Calculate the displacement current density inside the cable.
(ii) Integrate the displacement current density across the cross- section of the cable to find the total displacement current Id.
(iii) compare the conduction current I0 with the displacement current Id0.
View Solution
Knowledge Check
A long straight cable of length l is placed symmetrically along z-axis and has radius a(<<l). The cable consists of a thin wire and a co- axial conducting tube. An alternating current I(t)=I0 sin (2πvt). Flows down the central thin wire and returns along the co-axial conducting tube. the induced electric at a distance s from the wire inside the cable is
E(s,t)=μ0I0v cos (2πvt)In(sa)ˆk.
(i) Calculate the displacement current density inside the cable.
(ii) Integrate the displacement current density across the cross- section of the cable to find the total displacement current Id.
(iii) compare the conduction current I0 with the displacement current Id0.A2πλ2I0ln(as)sin(2πυt)ˆkB1λ2I0ln(as)sin(2πυt)ˆkCπλ2I0ln(as)sin(2πυt)ˆkDZeroA thermal power plant produed electric power of 600kW at 4000V, which is to be transported to a place 20 km away form the power plant for consumer's usage. It can be transported either directly with a cable of large current carrying capacity or by sing a combination of step-up and step-down transfprmers at the two ends. THe drawback of the direct transmission is the large energy dissipation. In the method wsing transformers, the dissipatiion is much smaller. In this method a step-up transformers is used at the plant side so that the current is reduced to a smaller value. At the consumers'end, a step-down transformer is used to supply power to the consumers at the specified lower voltage. It is reasonable to assume that the power cable is purely resostive and the transformers are ideal with power factor unity. All the currents and voltagementioned are values.
If hte direct transmission method with a cable of resistance 0.4(ω)km−1 is used, the power dissipation (in %) during transmission isA20B30C40D50
Two long parallel wires of negligible resistance are connected at one end to a resistance R and at the other end to a constant voltage source of voltage V. The distance between·the axes of the wires is η times greater than the cross-sectional radiµs of each wire. At what value of resistance R, does the resultant force of interaction between the wires will become zero?
View SolutionA long straight cable of length l is placed symmetrically along z-axis and has radius a(<<l). The cable consists of a thin wire and a co- axial conducting tube. An alternating current I(t)=I0 sin (2πvt). Flows down the central thin wire and returns along the co-axial conducting tube. the induced electric at a distance s from the wire inside the cable is
E(s,t)=μ0I0v cos (2πvt)In(sa)ˆk.
(i) Calculate the displacement current density inside the cable.
(ii) Integrate the displacement current density across the cross- section of the cable to find the total displacement current Id.
(iii) compare the conduction current I0 with the displacement current Id0.
View SolutionFigure 30-50 shows a rod of length L = 12.0 cm that is forced to move at constant speed v = 5.00 m/s along horizontal rails. The rod, rails, and connecting strip at the right form a conducting loop. The rod has resistance 0.400 Ω the rest of the loop has negligible resistance. A current i = 100 A through the long straight wire at distance a= 5.00 mm from the loop sets up a (nonuniform) magnetic field through the loop. Find the (a) emf and (b) current induced in the loop. (c) At what rate is thermal energy generated in the rod? (d) What is the magnitude of the force that must be applied to the rod to make it move at constant speed? (e) At what rate does this force do work on the rod?
View SolutionColumn I gives physical quantities based on a situation in which an ideal cell of emf V is connected across a cylindrical rod of uniform cross-section area and conductivity (sigma) as shown in figure E, J, phi and I are electric field at, current density through, electric flux through and current through shaded cross section repectively as shown in figure. Physical quantities in column-II are equal to those in column i Match the expression in Column I with the statement in Column II
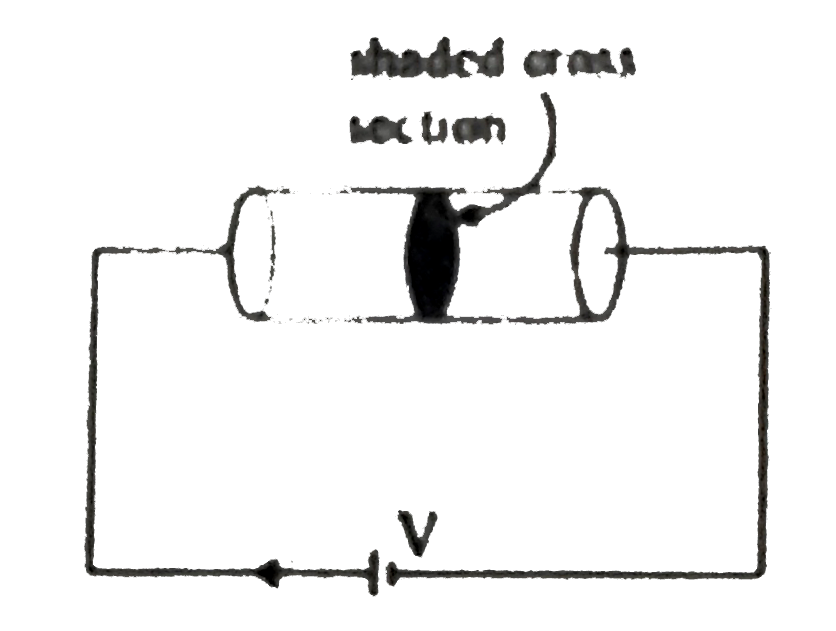
Column-IColumn-II(A)ϕi(P)Conductivity of rod(B)EJ(Q) Resistance of rod(C)σϕV(R)Resistivity of rod(D)Vσϕ(S)Power delivered to rod
View SolutionA ring of thin wire with active resistance R and inductance L rotates with constant angular velocity ω in the external uniform magneitce field perpendicular to the rotation axis. In the process , the flux of magnetic induction of external field across the ring varies with time as Φ=Φ0cosωt. Demonstrate that
(a) the inductive current in the ring varies with time as I=Imsin(ωt−φ), where Im=.mΦ/√R2+ω2L2 with tanφ=ωL/R,
(b) the mean mechanical is defined by the formula P=1/2ω2Φ20R/(R2+ω2L2).
View SolutionA thin wire ring of radius a and resitance r is located inside a long solenoid is equal to l, its cross-sectional radius , to b. At a certain moment the solenoid was connected to a source of a constant voltage V. The total resistance of the circuit is equal to R. Assuming the the radial force acting per unit length of the ring.
View Solution
