The equation of a wve travelling on a string stretched along the X-axis is given by
y=Ad−(xatT)2
a. Write the dimensions of A, a and T. b. Find the wave speed. c.In which direction is the wave travelling? d.Where is the maximum of the pulse located at t=T?Att=2T?
The correct Answer is:A, B, C, D
Given y=Ae−(xa+tT)2
a. [A]=[M0L1T0]
[T]=[M^0L^0T^-1]<br>[a]=[M0L1T0]
b. Wave speed v=lamda/T=a/T[Here lamda=a]<br>c.Ify=f(t+x/v)<br>→wavetravell∈g∈¬ativedirectionandify=f(t-x/v)<br>→wavetravell∈gpositivedirectio∈<br>So,y=Ae−[(xa)+(tT)]2
=Ae−1T[T+(xTa)]2
=Ae−1T[t+xV]
=Ae−f[t+xV]
Hence wave travelling is negative direction
d. Wave speed ltbr> V=at
Maximum pusle at t=T
is (aT)×T=a (negative x-axis)<br>Maξμmpuseatt=2T=(a/Txx2T)<br>=2a
(along negative x-axis)
so the wave travelling in negative x direction.
Topper's Solved these Questions
Similar Questions
The equation of a wave travelling on a string stretched along the X-axis is given by
y=Ae(−xa+tT)2
(a) Write the dimensions of A, a and T.
(b) Find the wave speed.
(c) In which direction is the wave travelling?
(d) Where is the maximum of the pulse located at t=T and at t=2T?
View SolutionThe equation of a wave travelling along the positive x-axis, as shown in figure at t=0 is given by
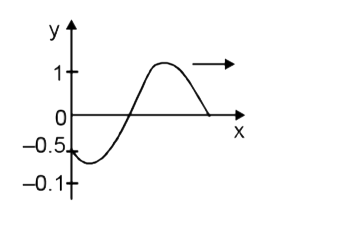
View Solution
Knowledge Check
The equation of a wave travelling on a stretched string along the x-axis is y=ae−(bx+ct). The direction of propagation of wave is
Aalong negative y-axisBalong positive y-axisCalong negative x-axisDalong positive x-axisThe equation of a wave travelling along the positive x-axis, as shown in figure at t=0 is given by :-
_E01_059_Q01.png) .Asin(kx−ωt+π6)Bsin(kx−ωt−π6)Csin(ωt−kx+π6)Dsin(ωt−kx−π6)
.Asin(kx−ωt+π6)Bsin(kx−ωt−π6)Csin(ωt−kx+π6)Dsin(ωt−kx−π6)the equation of a wave travelling along the positive x - axis ,as shown in figure at t = 0 is given by
 Asin(kx−ωt+π6)Bsin(kx−ωt−π6)Csin(ωt−kx+π6)Dsin(ωt−kx−π6)
Asin(kx−ωt+π6)Bsin(kx−ωt−π6)Csin(ωt−kx+π6)Dsin(ωt−kx−π6)
A travelling wave pulse is given by y=105+(x+2t)2
Here, xandy are in meter and t in second. In which direction and with what velocity is the pulse propagation. What is the ampitude of pulse?
View SolutionThe equation of a wave travelling on a string is y=(0.10mm)sin[3.14m−1)x+(314s−1)t]. (a) In which direction does the wave travel ? (b) Find the wave speed, the wavelength and the frequency of the wave. (c) What is the maximum displacement and the maximum speed of a portion of the string ?
View SolutionThe equation of a wave travelling on a stretched string is y = 4 sin 2π(t0.02−x100)
Here, x and y are in cm and t is in second. The speed of wave is
View SolutionThe equation of a transverse wave along a stretched string is given by
y=15sin2π(t0.04−x40)cm.
The velocity of the wave is
View SolutionThe equation of a progressive wave travelling on a strected string is y=10sin2π(t0.02−x100) where x and y are in cm and t is in sec. What is the speed of the wave?
View Solution
