The equivalent resistance of network of three 4Ω resistors can not be
12Ω
1.33Ω
6Ω
4Ω
The correct Answer is:D
To determine the equivalent resistance of a network of three 4-ohm resistors and identify which resistance cannot be achieved, we can analyze different combinations of these resistors.
1. Connect All Resistors in Series:
- When resistors are connected in series, the equivalent resistance (R_eq) is the sum of all resistances.
- Formula: Req=R1+R2+R3
- Calculation: Req=4Ω+4Ω+4Ω=12Ω
2. Connect All Resistors in Parallel:
- When resistors are connected in parallel, the equivalent resistance can be calculated using the formula:
- Formula: 1Req=1R1+1R2+1R3
- Calculation:
1Req=14Ω+14Ω+14Ω=34⇒Req=43Ω≈1.33Ω
3. Connect Two Resistors in Parallel and One in Series:
- First, calculate the equivalent resistance of the two resistors in parallel:
- Calculation:
1Rparallel=14Ω+14Ω=24=12⇒Rparallel=2Ω
- Now, add the third resistor in series:
- Calculation:
Req=Rparallel+R3=2Ω+4Ω=6Ω
4. Summary of Possible Equivalent Resistances:
- From the calculations:
- Series: 12 Ω
- Parallel: 1.33 Ω
- Two in parallel and one in series: 6 Ω
- The possible equivalent resistances are 12 Ω, 1.33 Ω, and 6 Ω.
5. Identify the Resistance that Cannot Be Achieved:
- The possible equivalent resistances we can achieve are 1.33 Ω, 6 Ω, and 12 Ω.
- The resistance that cannot be achieved with these combinations is 4 Ω.
Final Answer:
The equivalent resistance of the network of three 4-ohm resistors cannot be 4 Ω.
- When resistors are connected in series, the equivalent resistance (R_eq) is the sum of all resistances.
- Formula: Req=R1+R2+R3
- Calculation: Req=4Ω+4Ω+4Ω=12Ω
- When resistors are connected in parallel, the equivalent resistance can be calculated using the formula:
- Formula: 1Req=1R1+1R2+1R3
- Calculation:
1Req=14Ω+14Ω+14Ω=34⇒Req=43Ω≈1.33Ω
- First, calculate the equivalent resistance of the two resistors in parallel:
- Calculation:
1Rparallel=14Ω+14Ω=24=12⇒Rparallel=2Ω
- Now, add the third resistor in series:
- Calculation:
Req=Rparallel+R3=2Ω+4Ω=6Ω
- From the calculations:
- Series: 12 Ω
- Parallel: 1.33 Ω
- Two in parallel and one in series: 6 Ω
- The possible equivalent resistances are 12 Ω, 1.33 Ω, and 6 Ω.
- The possible equivalent resistances we can achieve are 1.33 Ω, 6 Ω, and 12 Ω.
- The resistance that cannot be achieved with these combinations is 4 Ω.
The equivalent resistance of the network of three 4-ohm resistors cannot be 4 Ω.
Topper's Solved these Questions
Similar Questions
Establish a relationship to determine the equivalent resistance R of a combination of three resistors having resistances R1,R2andR3 connected in series.
(b) Calculate the equivalent resistance R of a combination of three resistors of 2Ω,3Ωand6Ω joined in parallel.
View SolutionFind an expression for the equivalent resistance of three resistors joined in series.
View Solution
Knowledge Check
The equivalent resistance of network of three 4Ω resistors can not be
A12ΩB1.33ΩC6ΩD4ΩThe equivalent resistance of network of three 2Ω resistors can not be
A0.67B2ΩC3ΩD6ΩThe equivalent resistance of three equal resistances connected in series is 27Ω. There equivalent resistance when connected in parallel is
A54ΩB270ΩC3ΩD9Ω
Twelve equal resistors each R Ω are connected to from the edges of a cube . Find the equivalent resistance of the network.
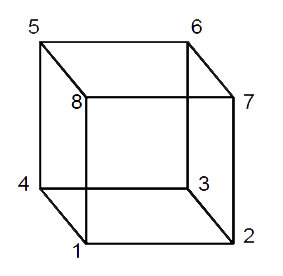
When current enters at 1 and leaves at 2
View SolutionTwelve equal resistors each R Ω are connected to from the edges of a cube . Find the equivalent resistance of the network.
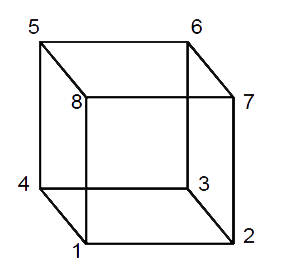
When current enters at 1 and leaves at 3
View SolutionFind an expression for equivalent resistance of three resistors joined in parallel.
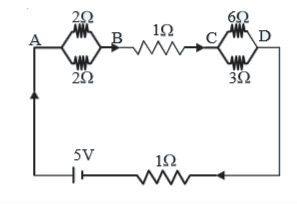
View SolutionA network of resistors is connected to a 5 V battery with internal resistance of 1Ω as shown in Fig. (a) Compute the equivalent resistance of the network. (6) Obtain the current in each resistor. (c) Obtain the voltage drops VBC and VCD
View SolutionTwelve equal resistors each R Ω are connected to from the edges of a cube . Find the equivalent resistance of the network.
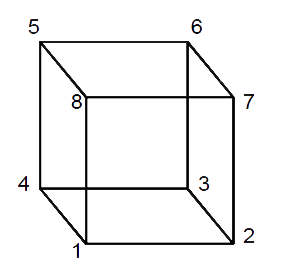
When current enters at 1 & leaves at 6 (body diagonal)
View Solution
