The figure, drawn here, shows the geometry of path differences for diffraction by a single slit of width a.
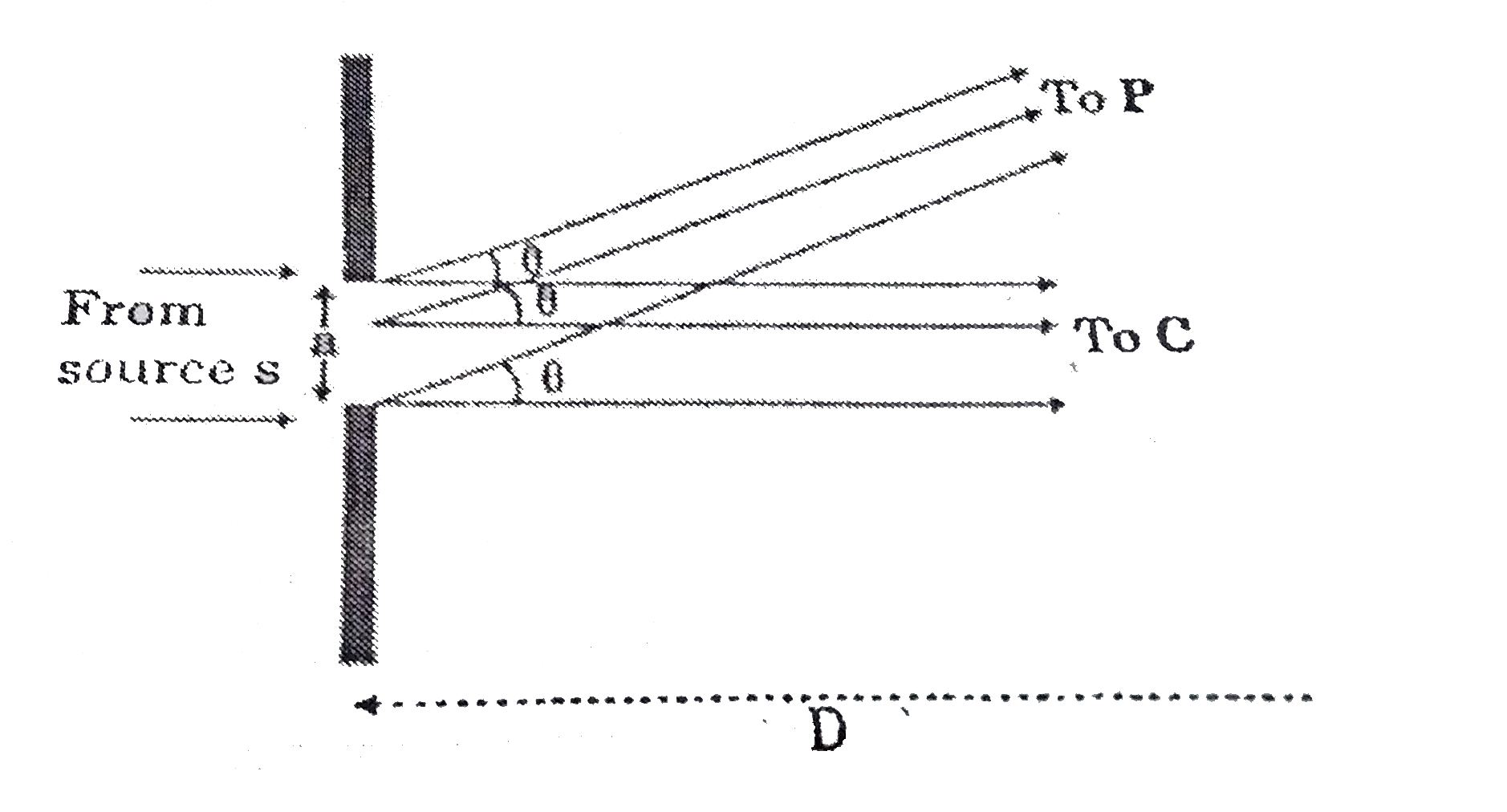
Given appropriate reasoning to explain why the intensity of light is
(i) maximum of the central point C on the screen.
(ii) (nearly) zero for point P on the screen when θ=λ/a.
Hence, write an expression for the total linear width of the central maxima on a screen kept at a distance D from the plane of the slit.
Video Solution
Text Solution
At center of screen C all wavelets :
(i) From slit meet in the same phase so they add constructively to produce a central maxima i.e., bright firnge.
(ii) When θ=λ/a, path difference from two halves of slit will be λ/2 i.e., wavelets from two halves reach at point P in opposite phase, giving a dark or minima.
(iii) β0=2Dλa.
|
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SECTIONS-D
4 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SECTIONS-E
4 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SECTIONS-B
6 Videos
- SAMPLE PAPER 2019BOOK - XII BOARDS PREVIOUS YEARCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
Knowledge Check
Angular width of central maxima of a single slit diffraction pattern is independent of
Aslit widthBfrequency of the light usedCwavelength of the light usedDdistance between slit and screenThe angular size of the central maxima due to a single slit diffraction is (a → slit width)
AλaB2λaC3λ2aDλ2aIn a single slit diffraction of light of wavelength λ by a slit of width e, the size of the central maximum on a screen at a distance b is
A(a) 2bλ+eB(b) 2bλeC(c) 2bλe=eD(d) 2bλe−e
The light of wavelength 600 nm is incident normally on a slit of width 3 mm. Calculate the linear width of central maximum on a screen kept m awy from the slit.
View SolutionAngular width of central maximum in diffraction at a single slit is……………. .
View SolutionThe light of wavelength 6000⋅A falls normally on a slit of width 2 mm. Calculate the linear width of central maxima on a screen kept 4 m away from the slit.
View SolutionThe angular width of the central maximum of the diffraction patternn in a single slit (of width a) experiment, with λ as the wavelenth of light, is
View SolutionIn the experiment of diffraction at a single slit, if the slit width is decreased, the wdith of the central maximum
View Solution
