The figure shows the variation of potential energy of a particle as a function pf x, the x-coordination of the region. It has been assumed that potential energy depends only on . For all other values is zero. i.e. for and .
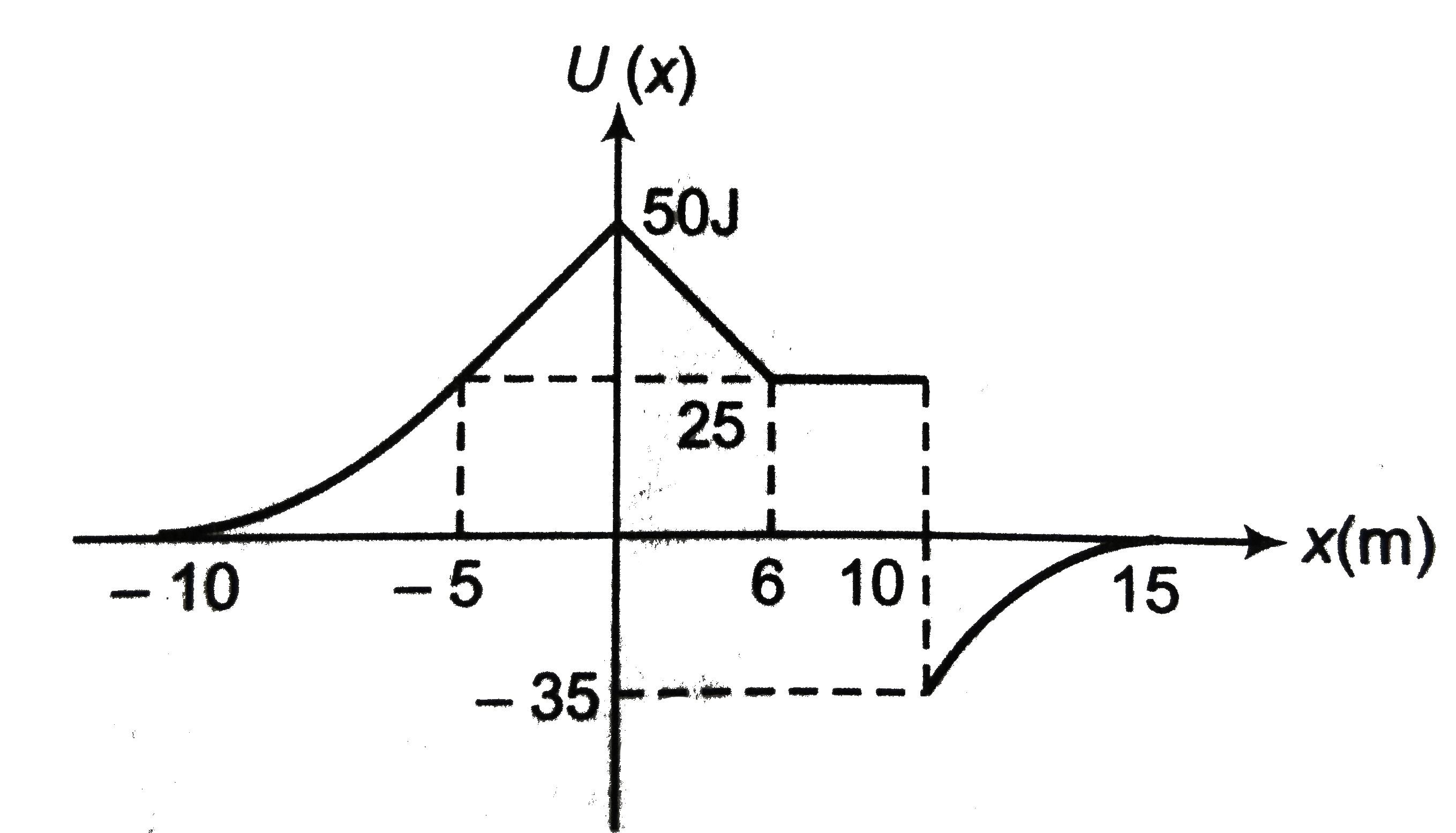
If total mechanical energy of the particle is , then it can found in the region
(a) and
(b) and
(c)
(d)
The correct Answer is:A
The concept used in solving these questions is that kinetic energy can never be negative. It would always be non-negative.
Total mechanical energy
Here if , then
For K to be non-negative, , which is the case for and .
Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Integer
Explore 14 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Archives (sinble Correct )
Explore 19 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Multiple Correct
Explore 25 Videos
- VECTORSBook:CENGAGE PHYSICS ENGLISHChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
The figure shows the variation of potential energy of a particle as a funcation of x, the x-coordinate of the region. It has been assumed that potential energy depends only on x. For all other values x,U is zero. i.e. forx<−10 and x>15,U=0.
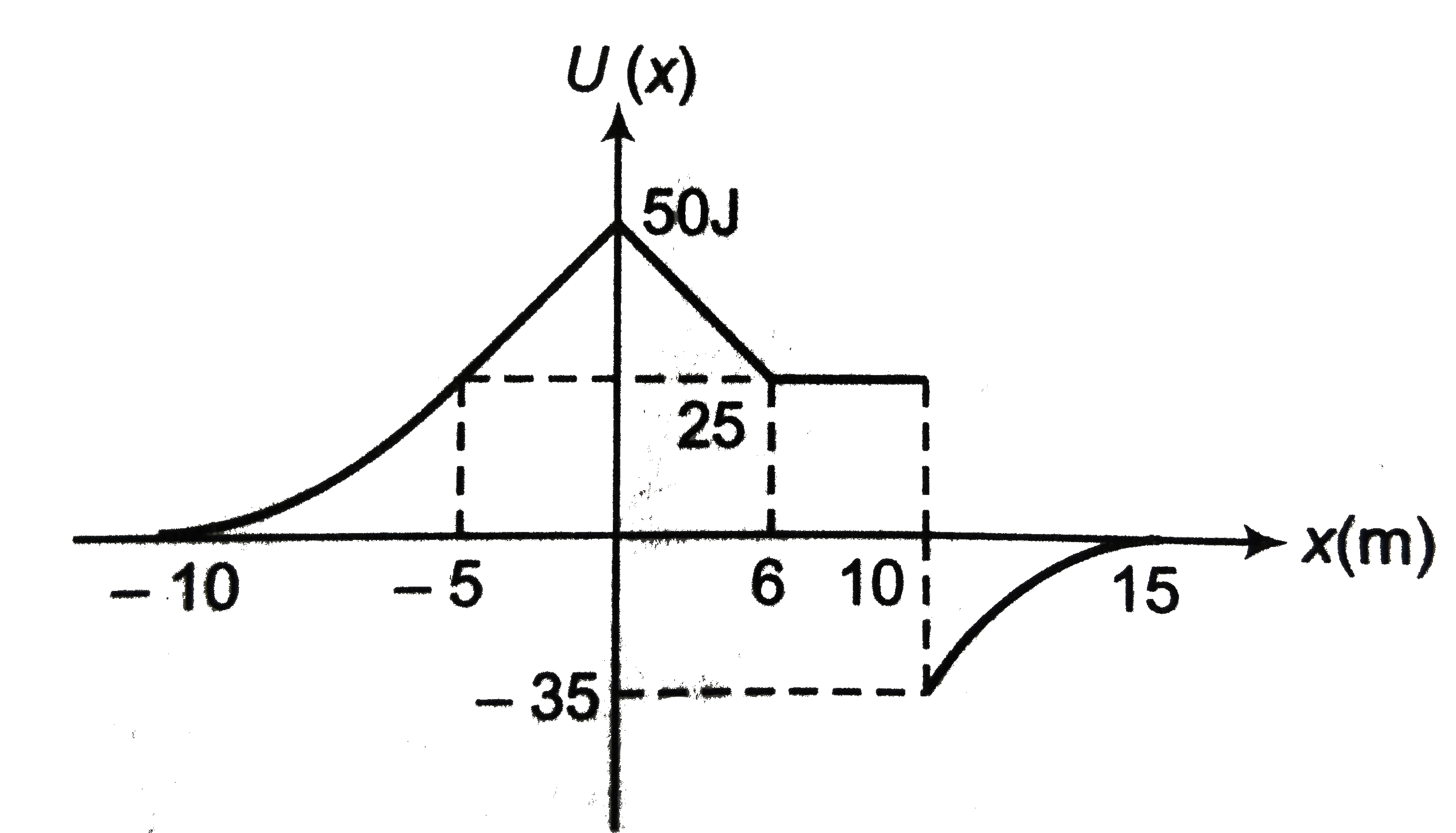
If total mechanical energy of the particle is −40J, then it can be found in region.
View SolutionFigure shows the variation of potential energy of a particle as a function of x, the x-coordinate of the region. It has been assumed that potential energy depends only on x. For all other values of x, U is zero, i.e., x←10 and x>15, U=0.
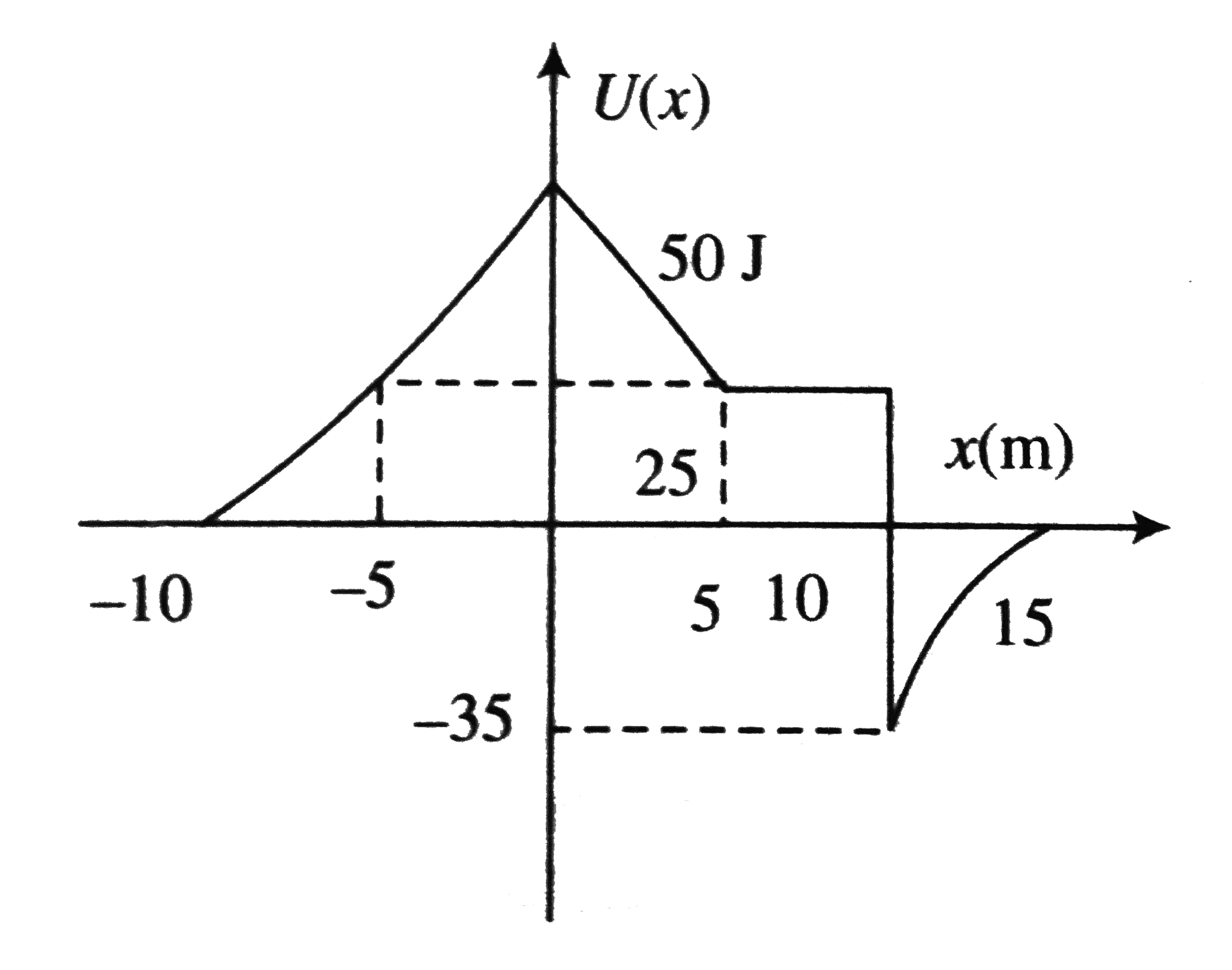
If the particle is isolated and its total mechanical energy is 60J, then
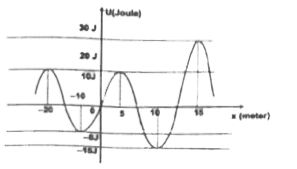
View SolutionThe given plot shows the variation of U, the potential energy of interaction between two particles with the distance separating them r,
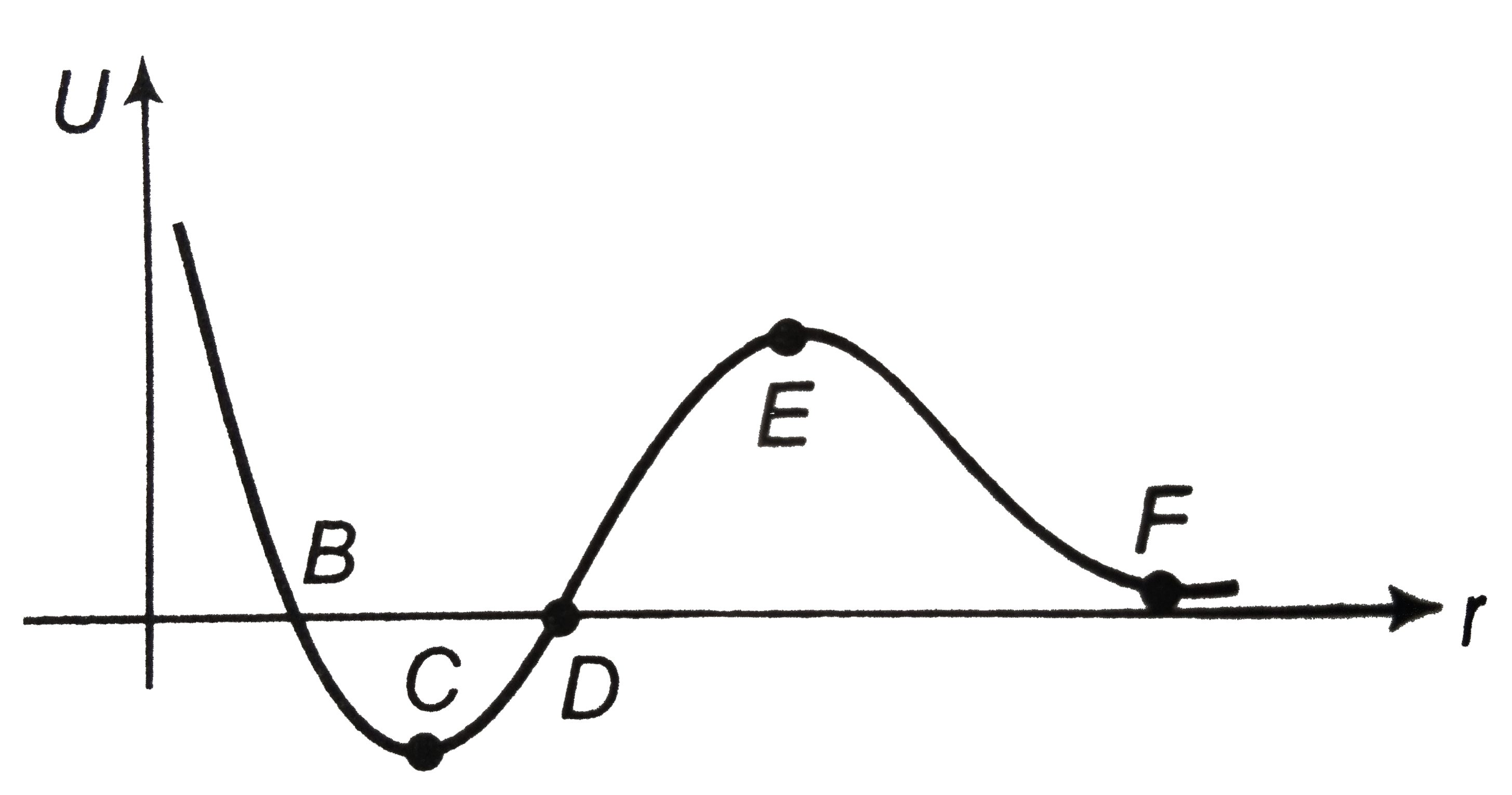
View SolutionThe given plot shows the variation of U, the potential energy of interaction between two particles with the distance separating them r,

View SolutionPotential energy curve U of a particle as function of the position of a particle is shown. The particle has total mechanical energy E of 3.0 joules. Then select correct alternative.
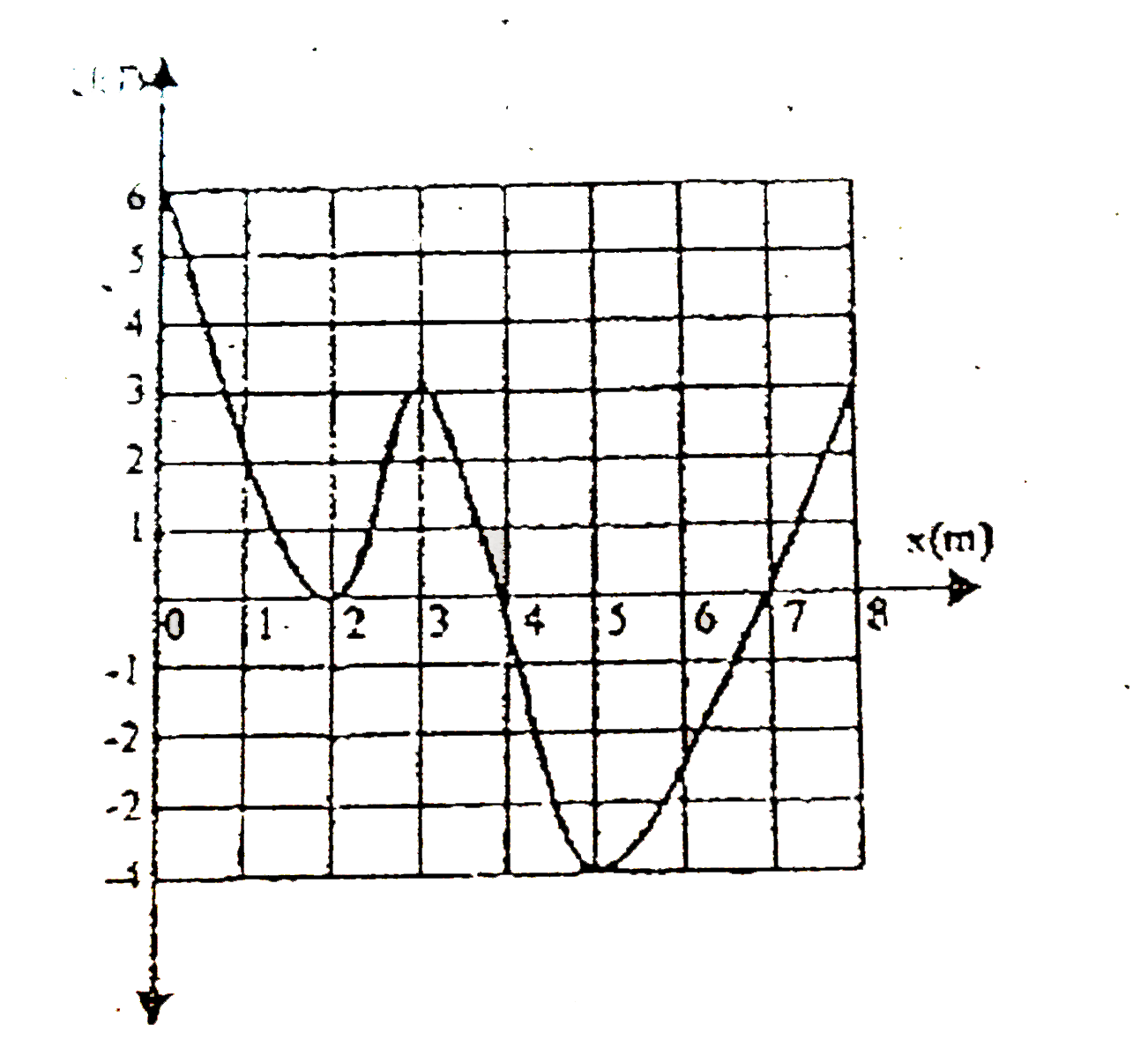
View SolutionThe potential energy of a particle of mass m is given by U=12kx2 for x<0 and U = 0 for x≥0. If total mechanical energy of the particle is E. Then its speed at x=√2Ek is
View SolutionThe potential energy of a particle varies with position X according to the relationU(x)=[(X33)−(3X22)+2X] then
View SolutionThe variation of potential energy of a particle of mass m = 5kg to its x-coordinate . The particle moves under the effect of this conservative force only along the x-axis. Then, choose the correct option.
View SolutionPotential energy of a particle is related to x coordinate by equation x2−2x . Particle will be in stable equilibrium at :
View Solution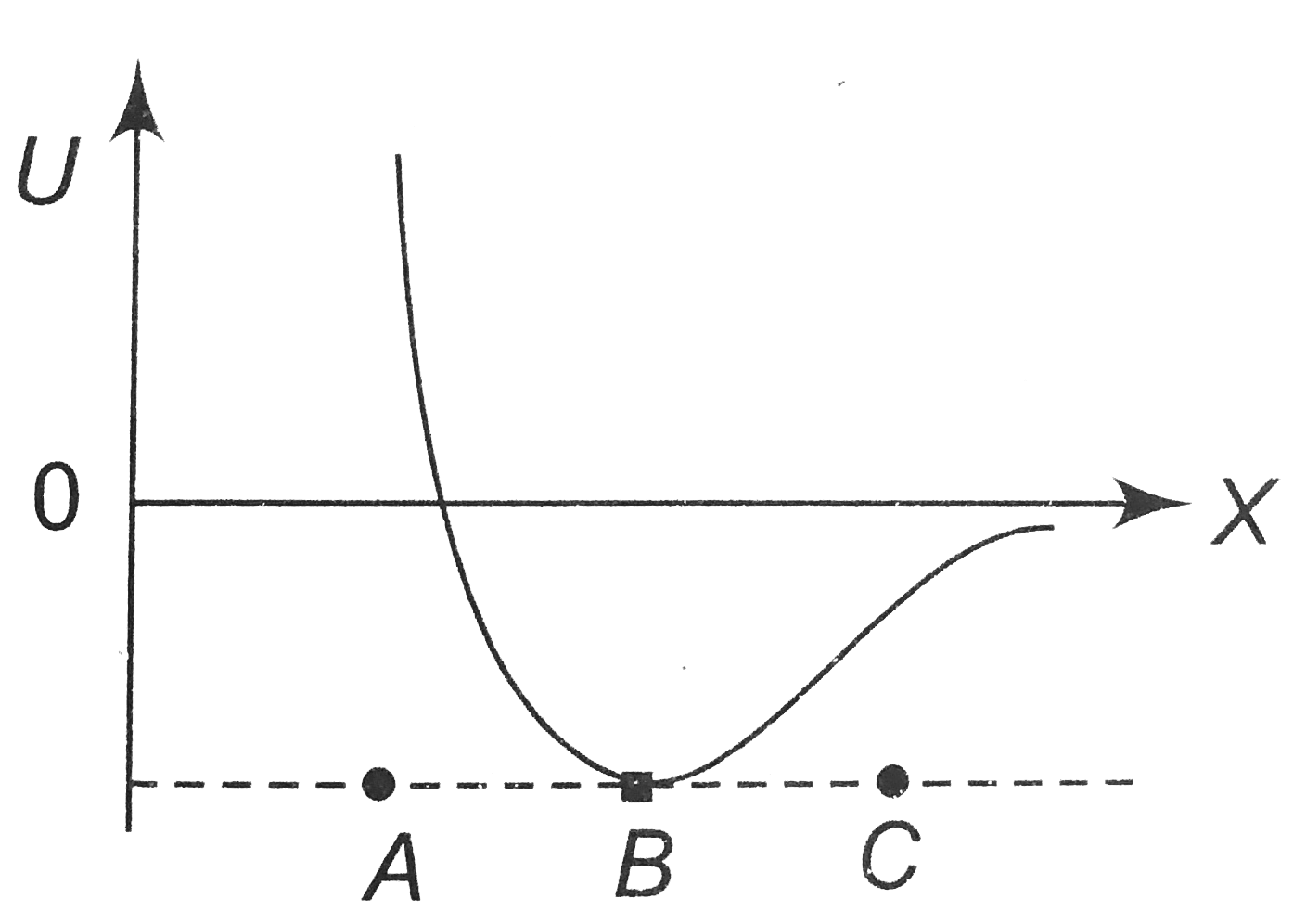
The potential energy U between two molecules as a function of the distance X between them has been shown in the figure. The two molecules are
View Solution