Potential energy of a particle is related to x coordinate by equation . Particle will be in stable equilibrium at :
The correct Answer is:B
To determine the position of stable equilibrium for a particle whose potential energy (U) is given by the equation U(x)=x2−2x, we will follow these steps:
Step 1: Find the Force
The force acting on the particle can be derived from the potential energy using the relationship:
F=−dUdx
First, we need to differentiate the potential energy function U(x).
Step 2: Differentiate the Potential Energy
We differentiate U(x)=x2−2x:
dUdx=2x−2
Now, substituting this into the force equation:
F=−dUdx=−(2x−2)=−2x+2
Step 3: Set the Force to Zero
To find the equilibrium position, we set the force equal to zero:
−2x+2=0
Solving for x:
2x=2⟹x=1
Step 4: Determine Stability of the Equilibrium
To determine whether this equilibrium is stable, we need to check the second derivative of the potential energy:
d2Udx2=ddx(2x−2)=2
Since d2Udx2=2 is positive, this indicates that the equilibrium at x=1 is stable.
Conclusion
The particle will be in stable equilibrium at x=1.
---
The force acting on the particle can be derived from the potential energy using the relationship:
F=−dUdx
First, we need to differentiate the potential energy function U(x).
We differentiate U(x)=x2−2x:
dUdx=2x−2
Now, substituting this into the force equation:
F=−dUdx=−(2x−2)=−2x+2
To find the equilibrium position, we set the force equal to zero:
−2x+2=0
Solving for x:
2x=2⟹x=1
To determine whether this equilibrium is stable, we need to check the second derivative of the potential energy:
d2Udx2=ddx(2x−2)=2
Since d2Udx2=2 is positive, this indicates that the equilibrium at x=1 is stable.
The particle will be in stable equilibrium at x=1.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - Level - 1 PARAGRAPH QUESTIONS3videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - LEVEL - 248videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - LEVEL - 0 - LONG ANSWER TYPE5videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)89videos
ELECTROSTATICS
- BOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )111videos
GASEOUS STATE & THERMODYNAMICS
Similar Questions
Potential energy of a particle at position x is given by U=(x2−4x)J. Which of the following is equilibrium position of the particle?
View SolutionPotential energy of a particle at position x is given by U=x2−5x. Which of the following is equilibrium position of the particle?
View SolutionIn the figure the variation of potential energy of a particle of mass m=2kg is represented w.r.t. its x-coordinate. The particle moves under the effect of this conservative force along the x-axis.
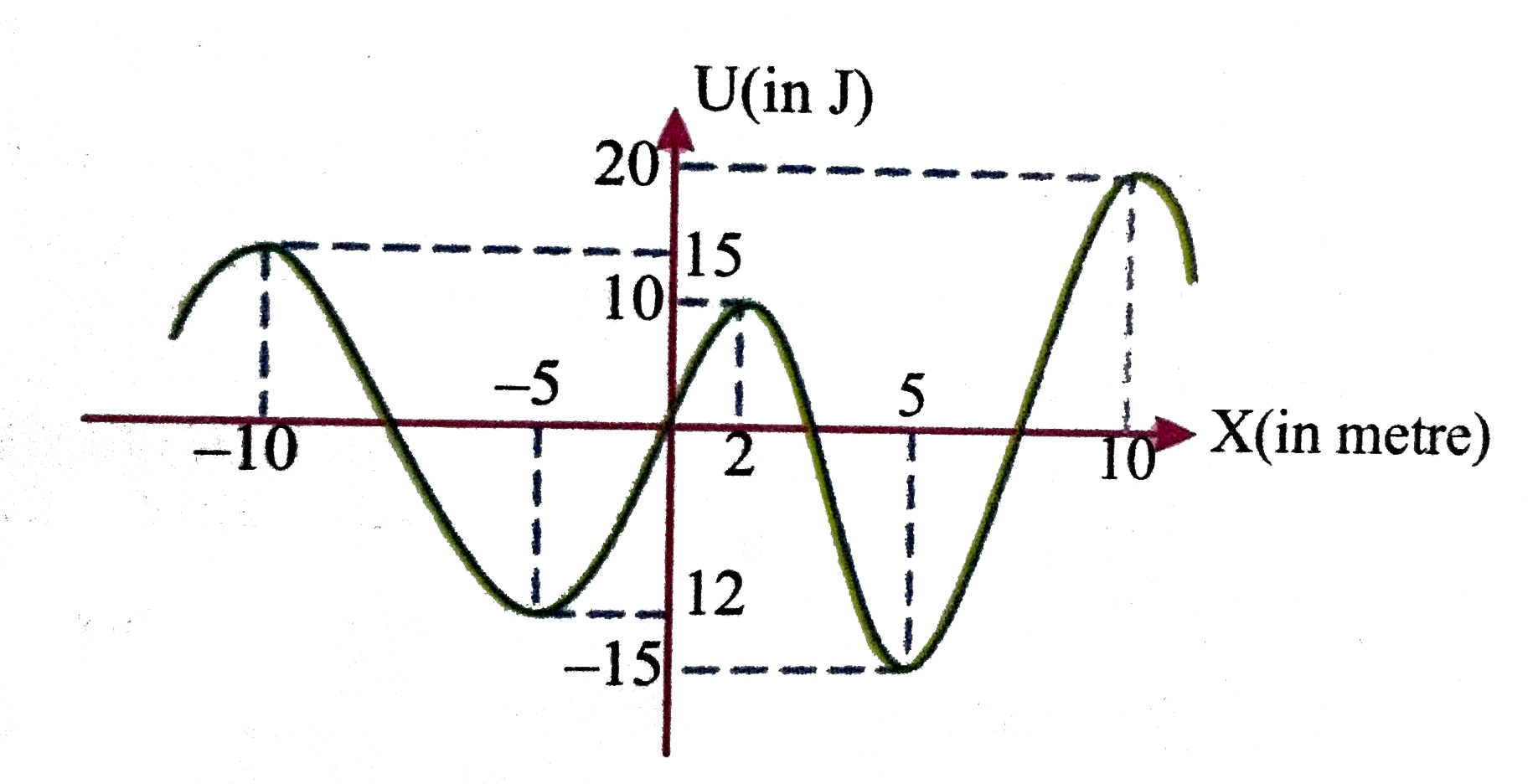
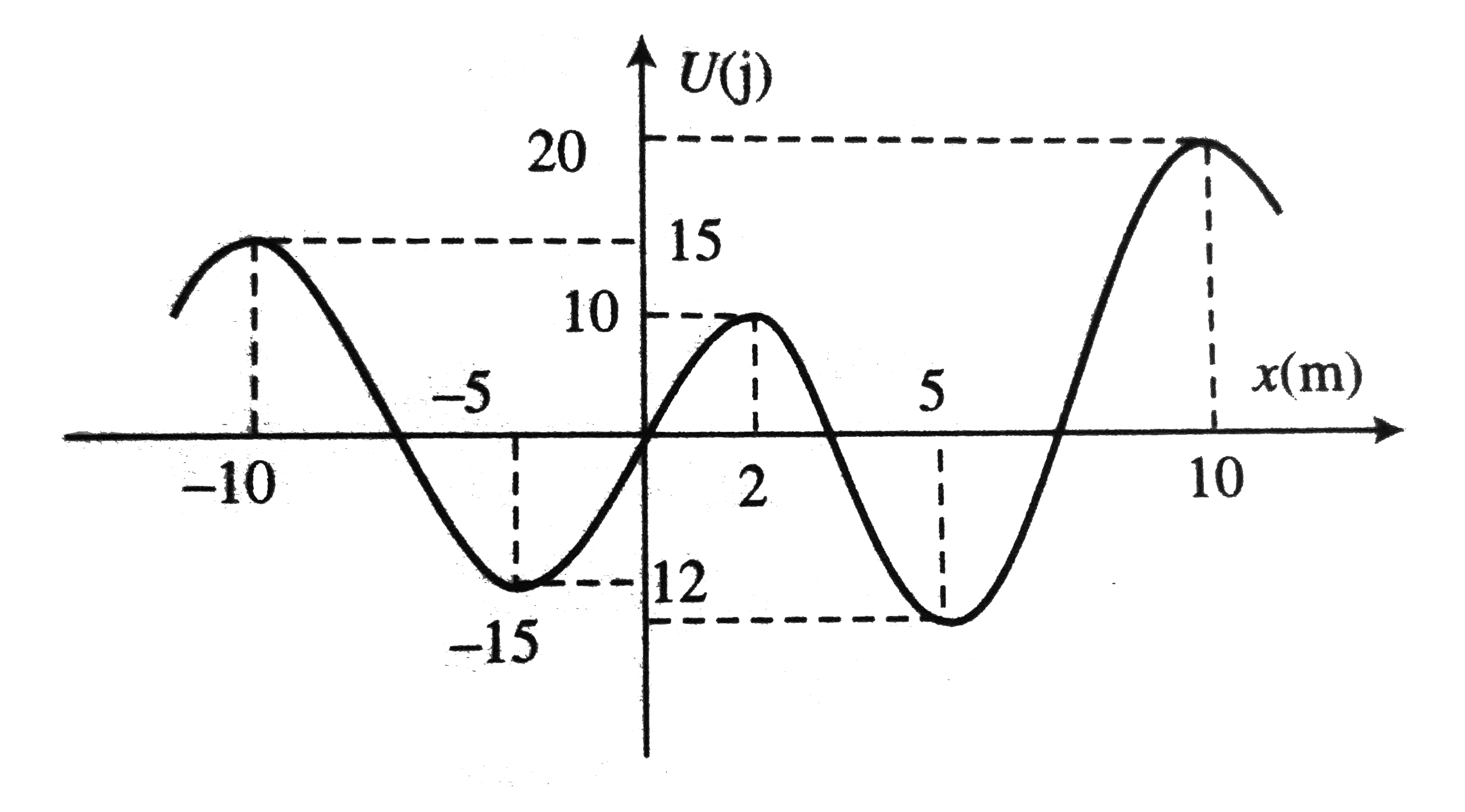
x=−5m and x=10m position of the particle are respectively ofView SolutionIn figure, the variation of potential energy of a particle of mass m=2kg is represented w.r.t its x-coordinate. The particle moves under the effect of the conservative force along the x-axis. Which of the following statements is incorrect about the particle?
 View Solution
View SolutionThe potential energy U(x) of a particle moving along x - axis is given by U(x)=ax−bx2. Find the equilibrium position of particle.
View SolutionThe potential energy of a particle under a conservative force is given by U(x)=(x2−3x) J. The equilibrium position of the particle is at
View SolutionThe potential enery of a particle varies with posiion x according to the relation U(x)=2x4−27x the point x=32 is point of
View SolutionIn the figure, the variation of potential energy of a particle of mass m = 2kg is represented with respect to its x-coordinate. The particle moves under the effect of this conservative force along the X-axis.
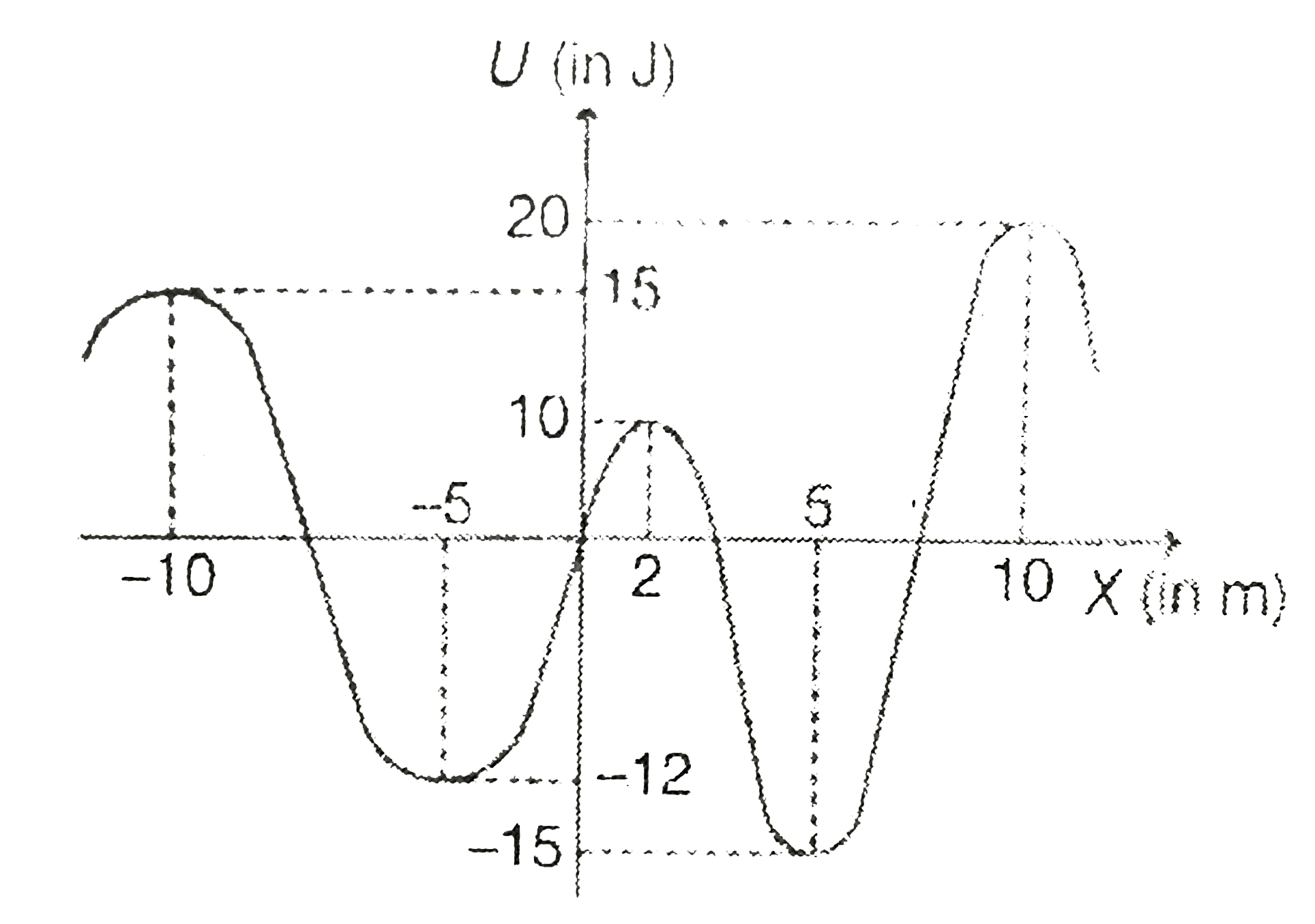
If the particle is released at x=2+Δ where Δ→0 (it is positive), then its maximum speed in subsequent motion will beView SolutionThe variation of potential energy of a particle of mass m = 5kg to its x-coordinate . The particle moves under the effect of this conservative force only along the x-axis. Then, choose the correct option.
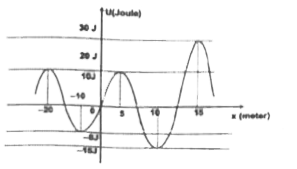 View Solution
View SolutionAssertion : A particle is under SHM along the x - axis. Its mean position is x=2, amplitude is A=2 and angular frequency ω. At t=0, particle is at origin, then x - co-ordinate versus time equation of the particle will be x=−2cosωt+2.
Reason : At t=0 , particle is at rest.View Solution

