The first excitation potential of a hypothetical hydrogen- like atom is 15V. Find the third excitation potential of the atom.
To solve the problem of finding the third excitation potential of a hypothetical hydrogen-like atom given that the first excitation potential is 15 V, we can follow these steps:
1. Understand the Concept of Excitation Potential:
- The excitation potential is the energy required to move an electron from a lower energy level to a higher energy level in an atom. For a hydrogen-like atom, the energy levels are quantized and can be calculated using the formula:
En=−E0n2
- Here, E0 is the ground state energy and n is the principal quantum number.
2. Identify the Given Information:
- The first excitation potential is given as 15 V, which corresponds to the transition from n=1 to n=2:
E2−E1=15V
3. Calculate the Energy Levels:
- For n=1:
E1=−E0
- For n=2:
E2=−E04
4. Set Up the Equation:
- Substitute E1 and E2 into the equation for the first excitation potential:
E2−E1=−E04−(−E0)=15V
- Simplifying this gives:
−E04+E0=15
- Combine the terms:
3E04=15
5. Solve for E0:
- Multiply both sides by 4:
3E0=60
- Divide by 3:
E0=20V
6. Calculate the Third Excitation Potential:
- The third excitation potential corresponds to the transition from n=1 to n=4:
E4−E1
- Calculate E4:
E4=−E016
- Substitute E1 and E4 into the equation:
E4−E1=−E016−(−E0)=−E016+E0
- Combine the terms:
E4−E1=E0−E016=16E016−E016=15E016
7. Substitute E0:
- Now substitute E0=20V:
E4−E1=15×2016=30016=18.75V
Final Answer:
The third excitation potential of the atom is 18.75V.
- The excitation potential is the energy required to move an electron from a lower energy level to a higher energy level in an atom. For a hydrogen-like atom, the energy levels are quantized and can be calculated using the formula:
En=−E0n2
- Here, E0 is the ground state energy and n is the principal quantum number.
- The first excitation potential is given as 15 V, which corresponds to the transition from n=1 to n=2:
E2−E1=15V
- For n=1:
E1=−E0
- For n=2:
E2=−E04
- Substitute E1 and E2 into the equation for the first excitation potential:
E2−E1=−E04−(−E0)=15V
- Simplifying this gives:
−E04+E0=15
- Combine the terms:
3E04=15
- Multiply both sides by 4:
3E0=60
- Divide by 3:
E0=20V
- The third excitation potential corresponds to the transition from n=1 to n=4:
E4−E1
- Calculate E4:
E4=−E016
- Substitute E1 and E4 into the equation:
E4−E1=−E016−(−E0)=−E016+E0
- Combine the terms:
E4−E1=E0−E016=16E016−E016=15E016
- Now substitute E0=20V:
E4−E1=15×2016=30016=18.75V
The third excitation potential of the atom is 18.75V.
Topper's Solved these Questions
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Solved Examples
23 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Exercise 4.1
15 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Single Correct
10 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer
5 Videos
Similar Questions
If first ionisation potential of a hypothetical atom is 16V, then the first excitation potential will be :
View SolutionMinimum excitation potential of Bohr's first orbit hydrogen atom is
View SolutionIf first excitation potential of a hydrogen-like atom is V electron volt, then the ionization energy of this atom will be:
View SolutionIf the I excitation potential of a hypothetical H-like is 162 V, then the value of II excitation energy is about :
View SolutionThe energy levels of a hypothetical one electron atom are shown in figure
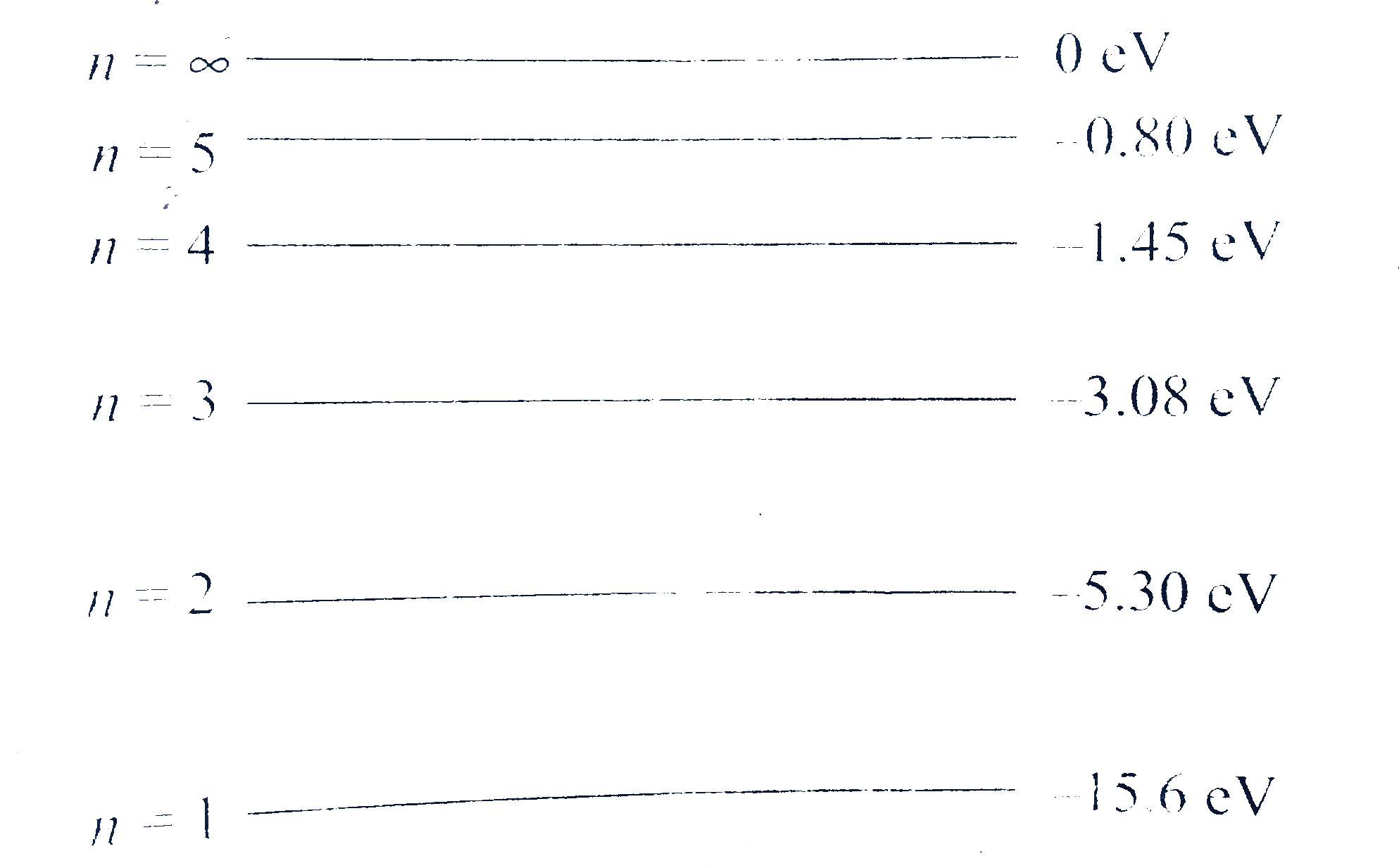
Find the ionization potential of the atom.
View SolutionThe energy level excitation potential of a hydrogen -like atom is shown in Figure

a Find the value of Z
b If initially the atom is in the ground state ,then
(i) determine its excitation potential, and
m (ii) determine its ionization potential.
c Can it absorbe a photom of 42eV?
d Can it absorbe a photom of 56eV?
e Calculate the radius of its first Bohr orbit.
f Calculate the kinectic and potential energy of an electron in the first orbit.
View SolutionThe energy levels of a hypotherical one electron atom are shown in figure
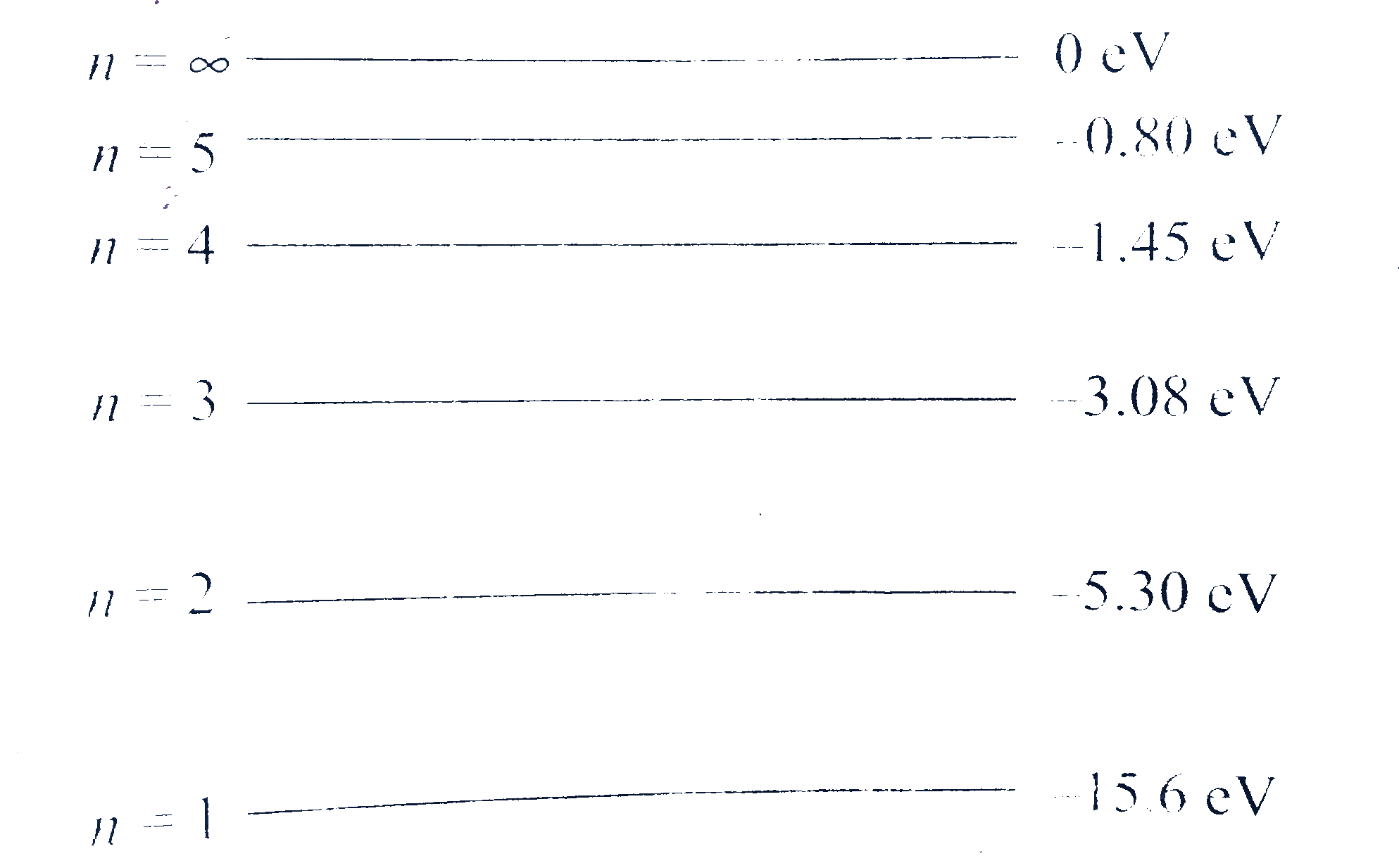
Find the excitation potential for the state n=3.
View SolutionThe ratio of the wave number corresponding to the 1st line of Lyman series of H− atom and 3rd line of Pashcan series of a hydrogen like sample is 9:16. Then find the third excitation potential in terms of volt for this H− like samples.
View SolutionIf the first excitation energy of a hydrogen - like atom is 27.3 eV , then ionization energy of this atom will be
View SolutionIf the binding energy of 2nd excited state of a hypothetical H-like atom is 12 eV, then the Correct option is/are :
View Solution
