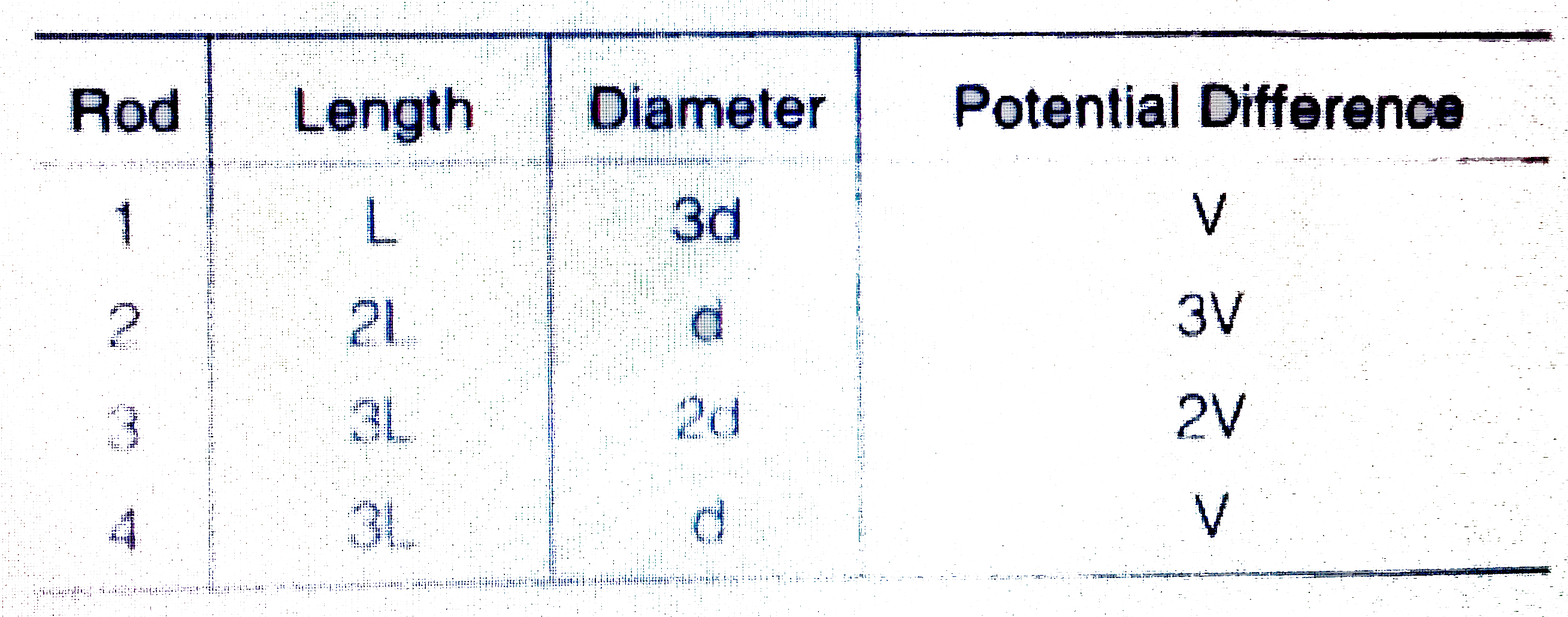
The following table gives the length of three copper rods, their diameters, and the potential differences between their ends. Rank the rods according to (a) the magnitude of the electric field within them, (b) the current density within them, and (c ) the drift speed of electrons through them, greates first.

a. E1=VL,E2=22L=VL,E3=2V3L.
Hecne, E1=E2>E3
c. Vd∝E. Hence, Vd1=Vd2>Vd3
b. I=neAvd=≠πd24=vd=meπ4vdd2
or I∝vdd2orI∝Ed2orI=Ked2
I1=KVL(3d)2=9Kvd2L,I2=KVLd2A
I3=K2V3L(2d)2=8KVd23L
Hence,I1>I3>I2.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Exercise 5.250videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Subjective29videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Solved Examples12videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits15videos
ELECTRIC CURRENT & CIRCUITS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
Similar Questions
the following table gives the lengths of four copper rods at the temperature ,their diameters and the potential differences between their ends.
 View Solution
View SolutionThe ratio of the diameters of two metallic rods of the same material is 2:1 and their lengths are in the ratio 1:4. If the temperature difference between their ends are equal, the rate of flow of heat in them will be in the ratio
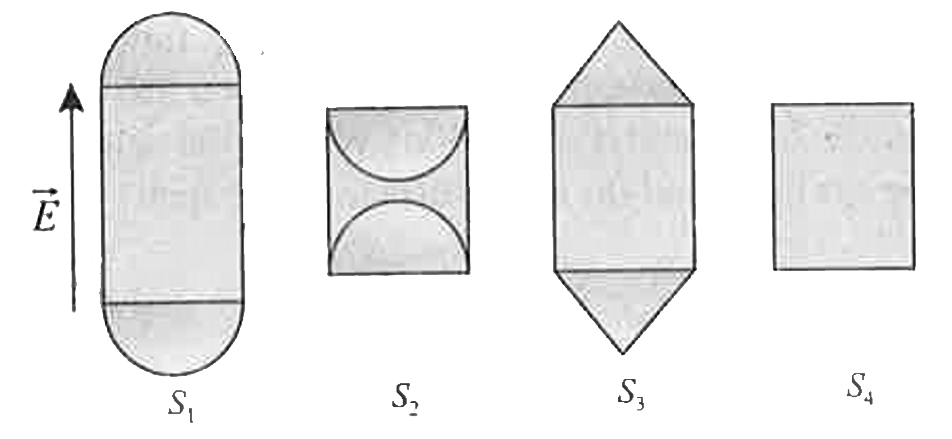
View SolutionFigure shows four Gaussion surfaces consisting of identical cylindrical midsections but different end caps. The surfaces central axis of each . Cylindrical midsection , the end caps have these shapes, S1 convex hemispheres S2 concave hermisphere S3 cones S4e flat disks. rank the surfaces acccording to (a) the net electric flux through them and (b) the electric flux through the top end caps , greatest first.
 View Solution
View SolutionIn a metal in the solid state, such as a copper wire, the atoms are strongly bound to one another and occupý fixed positions. Some electrons (called the conductor electrons) are free to move in the body of the metal while the other are strongly bound to their atoms. In good conductors, the number of free electrons is very large of the order of 1028 electrons per cubic metre in copper. The free electrons are in random motion and keep colliding with atoms. At room temperature, they move with velocities of the order of 105 m/s. These velocities are completely random and there is not net flow of charge in any directions. If a potential difference is maintained between the ends of the metal wire (by connecting it across a battery), an electric field is set up which accelerates the free electrons: These accelerated electrons frequently collide with the atoms of the conductor, as a result, they acquire a constant speed called the drift speed which is given by Ve= 1/enA where I = current in the conductor due to drifting electrons, e = charge of electron, n = number of free electrons per unit volume of the conductor and A = area of cross-section of the conductor. A uniform wire of length 2.0 m and cross-sectional area 10−7m2 carries a current of 1.6 A. If there are 1028 free electrons per m in copper, the drift speed of electrons in copper is
View SolutionIn a metal in the solid state, such as a copper wire, the atoms are strongly bound to one another and occupý fixed positions. Some electrons (called the conductor electrons) are free to move in the body of the metal while the other are strongly bound to their atoms. In good conductors, the number of free electrons is very large of the order of 1028 electrons per cubic metre in copper. The free electrons are in random motion and keep colliding with atoms. At room temperature, they move with velocities of the order of 105 m/s. These velocities are completely random and there is not net flow of charge in any directions. If a potential difference is maintained between the ends of the metal wire (by connecting it across a battery), an electric field is set up which accelerates the free electrons: These accelerated electrons frequently collide with the atoms of the conductor, as a result, they acquire a constant speed called the drift speed which is given by Ve= 1/enA where I = current in the conductor due to drifting electrons, e = charge of electron, n = number of free electrons per unit volume of the conductor and A = area of cross-section of the conductor. A constant potential difference is maintained between the ends of a conductor having nonuniform cross-section. Which of the following quantities will not change along the length of the conductor
View SolutionIn a metal in the solid state, such as a copper wire, the atoms are strongly bound to one another and occupý fixed positions. Some electrons (called the conductor electrons) are free to move in the body of the metal while the other are strongly bound to their atoms. In good conductors, the number of free electrons is very large of the order of 1028 electrons per cubic metre in copper. The free electrons are in random motion and keep colliding with atoms. At room temperature, they move with velocities of the order of 105 m/s. These velocities are completely random and there is not net flow of charge in any directions. If a potential difference is maintained between the ends of the metal wire (by connecting it across a battery), an electric field is set up which accelerates the free electrons: These accelerated electrons frequently collide with the atoms of the conductor, as a result, they acquire a constant speed called the drift speed which is given by Ve= 1/enA where I = current in the conductor due to drifting electrons, e = charge of electron, n = number of free electrons per unit volume of the conductor and A = area of cross-section of the conductor. A current of 1 A flows through a copper wire. The number of electrons passing through any cross-section of the wire in 1.6 sec is (charge of a electron = 1.6 xx 10^(-19 c).
View SolutionA currrent I is passed through a silver strip of width d and area of cross section A. The number of free electrons per unit volume is n. (a) Find the drift velocity v of the electrons. (b) If a magnetic field B exists in the region as shown in what is the average magnetic force on the free electrons? (c) Due to the magnetic force, the free electrons get accumulated on one side of the conductor along its length. This produces a transverse electric field in the conductor which opposes the magnetic force on the electrons. Find the magnitude of the electric field which will be the potential diference developed across the width of the conductor due to the electron- accumulation? The appearance of a transverse emf, when a current-carrying wire is placed in a magnetic field, is called hall effect.
 View Solution
View SolutionIn a metal in the solid state, such as a copper wire, the atoms are strongly bound to one another and occupý fixed positions. Some electrons (called the conductor electrons) are free to move in the body of the metal while the other are strongly bound to their atoms. In good conductors, the number of free electrons is very large of the order of 1028 electrons per cubic metre in copper. The free electrons are in random motion and keep colliding with atoms. At room temperature, they move with velocities of the order of 105 m/s. These velocities are completely random and there is not net flow of charge in any directions. If a potential difference is maintained between the ends of the metal wire (by connecting it across a battery), an electric field is set up which accelerates the free electrons: These accelerated electrons frequently collide with the atoms of the conductor, as a result, they acquire a constant speed called the drift speed which is given by Ve= 1/enA where I = current in the conductor due to drifting electrons, e = charge of electron, n = number of free electrons per unit volume of the conductor and A = area of cross-section of the conductor.
If no potential difference is maintained between the ends of a conductorView SolutionIn a metal in the solid state, such as a copper wire, the atoms are strongly bound to one another and occupý fixed positions. Some electrons (called the conductor electrons) are free to move in the body of the metal while the other are strongly bound to their atoms. In good conductors, the number of free electrons is very large of the order of 1028 electrons per cubic metre in copper. The free electrons are in random motion and keep colliding with atoms. At room temperature, they move with velocities of the order of 105 m/s. These velocities are completely random and there is not net flow of charge in any directions. If a potential difference is maintained between the ends of the metal wire (by connecting it across a battery), an electric field is set up which accelerates the free electrons: These accelerated electrons frequently collide with the atoms of the conductor, as a result, they acquire a constant speed called the drift speed which is given by Ve= 1/enA where I = current in the conductor due to drifting electrons, e = charge of electron, n = number of free electrons per unit volume of the conductor and A = area of cross-section of the conductor. The drift speed of free electrons in a conductor depends upon
View SolutionIn a metal in the solid state, such as a copper wire, the atoms are strongly bound to one another and occupý fixed positions. Some electrons (called the conductor electrons) are free to move in the body of the metal while the other are strongly bound to their atoms. In good conductors, the number of free electrons is very large of the order of 1028 electrons per cubic metre in copper. The free electrons are in random motion and keep colliding with atoms. At room temperature, they move with velocities of the order of 105 m/s. These velocities are completely random and there is not net flow of charge in any directions. If a potential difference is maintained between the ends of the metal wire (by connecting it across a battery), an electric field is set up which accelerates the free electrons: These accelerated electrons frequently collide with the atoms of the conductor, as a result, they acquire a constant speed called the drift speed which is given by Ve= 1/enA where I = current in the conductor due to drifting electrons, e = charge of electron, n = number of free electrons per unit volume of the conductor and A = area of cross-section of the conductor. Choose the current statements
View Solution

