The force on a particle is directed along an x axis and given by F=F0(x/x0−1). Find the work done by the force in moving the particle from x=0 to x=2x0 by (a) plotting F(x) and measuring the work from the graph and (b) integrating F(x).
The correct Answer is:(a) Zero; (b) Zero
To solve the problem of finding the work done by the force F=F0(xx0−1) as the particle moves from x=0 to x=2x0, we will follow two approaches: (a) plotting the graph of F(x) and measuring the work done from the graph, and (b) integrating F(x).
Part (a): Plotting the Graph
1. Identify the Force Function: The force function is given as:
F(x)=F0(xx0−1)
2. Determine Key Points:
- At x=0:
F(0)=F0(0x0−1)=−F0
- At x=x0:
F(x0)=F0(x0x0−1)=0
- At x=2x0:
F(2x0)=F0(2x0x0−1)=F0
3. Plot the Points:
- Plot the points (0,−F0), (x0,0), and (2x0,F0) on a graph with x on the horizontal axis and F on the vertical axis.
4. Draw the Graph: Connect the points to form a straight line from (0,−F0) to (x0,0) and then from (x0,0) to (2x0,F0).
5. Calculate the Area Under the Curve:
- The area under the curve from x=0 to x=x0 (triangle with base x0 and height −F0):
W1=12×base×height=12×x0×(−F0)=−12F0x0
- The area under the curve from x=x0 to x=2x0 (triangle with base x0 and height F0):
W2=12×base×height=12×x0×F0=12F0x0
6. Total Work Done:
W=W1+W2=−12F0x0+12F0x0=0
Part (b): Integrating the Force
1. Set Up the Integral:
The work done W is given by the integral of the force over the displacement:
W=∫2x00F(x)dx=∫2x00F0(xx0−1)dx
2. Integrate:
W=F0∫2x00(xx0−1)dx
=F0(1x0⋅x22−x)2x00
=F0(1x0⋅(2x0)22−2x0)−F0(0−0)
=F0(2x20x0−2x0)=F0(2x0−2x0)=0
Conclusion
The work done by the force in moving the particle from x=0 to x=2x0 is 0.
F(x)=F0(xx0−1)
- At x=0:
F(0)=F0(0x0−1)=−F0
- At x=x0:
F(x0)=F0(x0x0−1)=0
- At x=2x0:
F(2x0)=F0(2x0x0−1)=F0
- Plot the points (0,−F0), (x0,0), and (2x0,F0) on a graph with x on the horizontal axis and F on the vertical axis.
- The area under the curve from x=0 to x=x0 (triangle with base x0 and height −F0):
W1=12×base×height=12×x0×(−F0)=−12F0x0
- The area under the curve from x=x0 to x=2x0 (triangle with base x0 and height F0):
W2=12×base×height=12×x0×F0=12F0x0
W=W1+W2=−12F0x0+12F0x0=0
The work done W is given by the integral of the force over the displacement:
W=∫2x00F(x)dx=∫2x00F0(xx0−1)dx
W=F0∫2x00(xx0−1)dx
=F0(1x0⋅x22−x)2x00
=F0(1x0⋅(2x0)22−2x0)−F0(0−0)
=F0(2x20x0−2x0)=F0(2x0−2x0)=0
The work done by the force in moving the particle from x=0 to x=2x0 is 0.
Topper's Solved these Questions
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)
59 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (More than one choice correct type)
10 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - CHECKPOINT
6 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Integer Type)
4 Videos
Similar Questions
A force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from

View SolutionA force F is related to the position of a particle by the relation F=(10x2)N . Find the work done by the force when the particle moves from x=2m→x=4m.
View Solution
Knowledge Check
A force F acting on a particle varies with the position x as shown in the graph. Find the work done by the force in displacing the particle from x=−a to x=+2a.
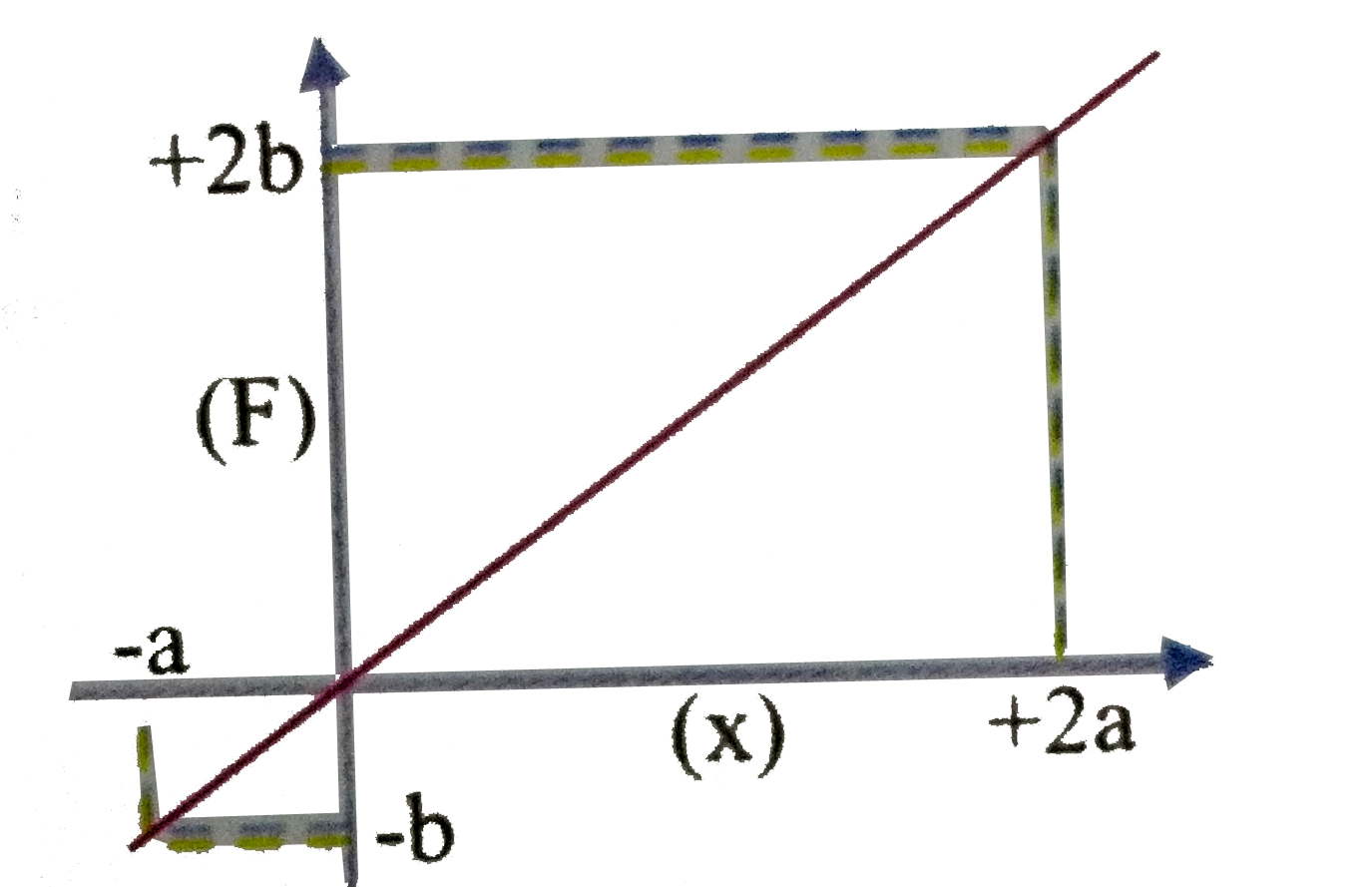 .A3ab2B4ab2C23abD24ab
.A3ab2B4ab2C23abD24abA block is constrained to move along xaxis under a force F=−(2x)N. Find the work done by the force when the block is displaced from x=2m to x=4m
A12JB8JC−12JD−8JA force F=(2+x) acts on a particle in x-direction where F is in newton and x in metre. Find the work done by this force during a displacement form 1. 0 m to x = 2.0 m.
A1.5JB2.5JC3.5JD4.5J
A force F=(5+2x) acts on a particle in x direction where F is in newtown and x is meter. Find the work done by this force during displacement from x=0 to x=1m.
View SolutionA force F=a+bx acts on a particle in x-direction, where a and b are constants. Find the work done by this force during the displacement from x1 to x2.
View SolutionA force F=(15+0.50x) acts on a particle in the X-direction ,where F is in newton and x in metre Find the work done ' by this force during a displacement from x=0 to x=2.0 m .
View SolutionA force F=a+b x acts on a particle in the X-direction, where a and b are constants. Find the work done by this force during a displacement from x=0 to x=d/
View SolutionA variable force F acts along the x - axis given by F=(3x2)−2x+1N. The work done by the force when a particle of mass 100 g moves from x = 50 cm to x = 100 cm is
View Solution
