The fraction $f$ of radioactive material that has decayed in time $t$ , varies with time $t$ . The correct variation id given by the curve.
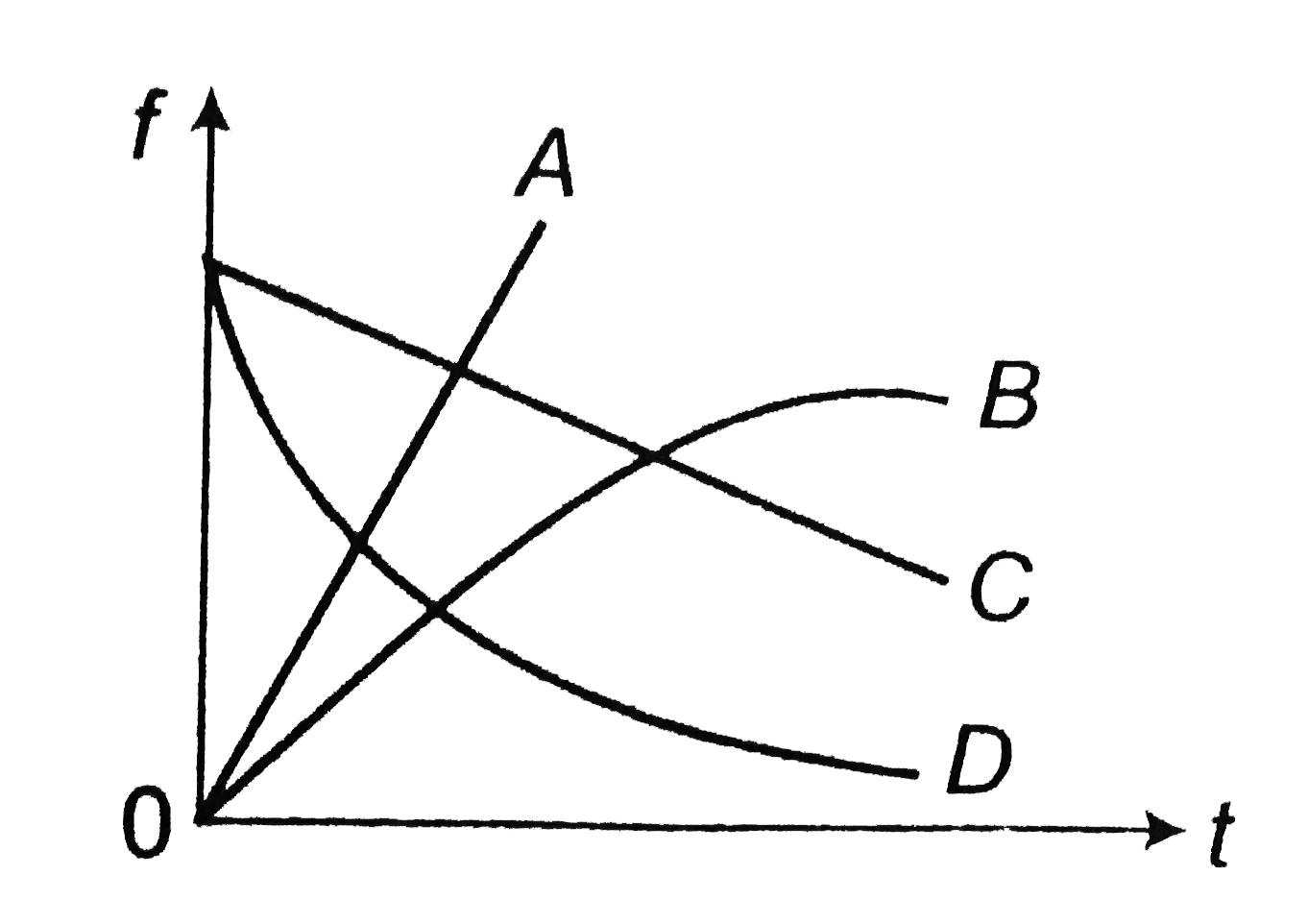$The fraction f of radioactive material that has decayed in time t, varies with time t. The correct variation id given by the curve. .$ .

A

A

B

B

C

C

D

D

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

(b) Number of atoms undecayed $N = N_{0} e^{- λ t}$
Number of atoms decayed $= N_{0} - N = N_{0} (1 - e^{- λ t})$
rArr Decayed fraction $f = \frac{N_{0} - N}{N_{0}} = 1 - e^{- λ t}$
i.e, fraction will rise up to $1$ . Following exponential path as shown in graph (B).

|

Updated on:21/07/2023

Class 12 PHYSICS NUCLEI

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The fraction of a radioactive material which remains active after time t is $9 / 16$ . The fraction which remains active after time $t / 2$ will be .
A $\frac{4}{5}$
B $\frac{7}{8}$
C $\frac{3}{5}$
D $\frac{3}{4}$
Question 2 - Select One
$20 %$ radioactive sample decay in time t. How much sample decay in time 2t ?
A $40 %$
B $36 %$
C $44 %$
D $80 %$
Question 3 - Select One
The equations $\frac{d N}{d t} = - λ N$ and $N = N_{0} e^{- λ t}$ describes how the number N of undecayed atoms in a sample of radioactive material, which initially (at $t = 0$ ) contained $N_{0}$ undecayed atoms, varies with time t. Which one of the following statements about $λ$ is correct ?
A $λ δ t$ gives the fraction of atoms present which will decay in the next small time interval $δ t$
B $λ$ is the time needed for N to fall from N0 to the value $N_{0} / e$
C $λ$ is the number of atoms left after a time equal to e second.
D $λ$ is the chance that any one atom will still be undecayed after one second.

A2Z-NUCLEAR PHYSICS-Radioactive Disintegration

Home
Ask Doubt
Profile