If 'f' denotes the ratio of the number of nuclei decayed (Nd) to the number of nuclei at t=0(N0) then for a collection of radioactive nuclei, the rate of change of 'f' with respect to time is given as :
[λ is the radioactive decay constant]
−λ(1−e−λt)
λ(1−e−λt)
λe−λt
−λe−λt
The correct Answer is:C
To solve the problem, we need to find the rate of change of the ratio of the number of decayed nuclei f with respect to time t. Let's break it down step by step.
1. Define the Variables:
- Let N0 be the initial number of nuclei at t=0.
- Let Nd be the number of nuclei that have decayed by time t.
- The ratio f is defined as:
f=NdN0
2. Relate Nd and N:
- The number of nuclei remaining at time t can be expressed using the radioactive decay formula:
N=N0e−λt
- The number of decayed nuclei Nd can be expressed as:
Nd=N0−N=N0−N0e−λt=N0(1−e−λt)
3. Substitute Nd into the equation for f:
- Now substituting Nd into the equation for f:
f=NdN0=N0(1−e−λt)N0=1−e−λt
4. Differentiate f with respect to t:
- To find the rate of change of f with respect to time, we differentiate f:
dfdt=ddt(1−e−λt)
- The derivative of a constant (1) is 0, and using the chain rule for the exponential function:
dfdt=0−(−λe−λt)=λe−λt
5. Final Result:
- Thus, the rate of change of f with respect to time t is:
dfdt=λe−λt
Conclusion:
The correct answer is:
dfdt=λe−λt
- Let N0 be the initial number of nuclei at t=0.
- Let Nd be the number of nuclei that have decayed by time t.
- The ratio f is defined as:
f=NdN0
- The number of nuclei remaining at time t can be expressed using the radioactive decay formula:
N=N0e−λt
- The number of decayed nuclei Nd can be expressed as:
Nd=N0−N=N0−N0e−λt=N0(1−e−λt)
- Now substituting Nd into the equation for f:
f=NdN0=N0(1−e−λt)N0=1−e−λt
- To find the rate of change of f with respect to time, we differentiate f:
dfdt=ddt(1−e−λt)
- The derivative of a constant (1) is 0, and using the chain rule for the exponential function:
dfdt=0−(−λe−λt)=λe−λt
- Thus, the rate of change of f with respect to time t is:
dfdt=λe−λt
The correct answer is:
dfdt=λe−λt
Topper's Solved these Questions
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - PHYSICS (SECTION-B)40videos
JEE MAINS 2021
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - PHYSICS (SECTION - A)40videos
JEE MAINS 2021
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2020EXERCISE - PHYSICS246videos
JEE MAINS 2020
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -B)10videos
JEE MAINS 2022
Similar Questions
Knowledge Check
- Question 1 - Select One
The rate at which a particular decay process occurs in a radio active sample, is proportional to the number of radio active nuclei present. If N is the number of radio active nuclei present at some instant, the rate of change of N is dNdt=−λN.
_E01_161_Q01.png)
Consider radioavtive decay of A to B which may further decay, either to X or to Y, λ1,λ2 and λ3 are decay constants for A to B decay, B to X decay and B of Y decay respectively. If at t=0 number of nuclei of A, B, X and Y are N0,N0, zero and zero respectively and N1,N2,N3,N4 are number of nuclei A,B,X and Y at any intant.
At t=∞, which of the following is incorrect ?AN2=0BN3=N0λ2λ2+λ3CN4=2N0λ3λ2+λ3DN3+N4+N1+N2=2N0 - Question 2 - Select One
The half life of a radioactive substance is T0. At t=0,the number of active nuclei are N0. Select the correct alternative.
AThe number of nuclei decayed in time internal 0−t is N0e−λtBThe number of nuclei decays in time interval 0−t is N0(1−e−λt)CThe probability that a radioactive nuclei does not decay in interval 0−t is e−λtDThe probability that a radioactive nuclei does not decay in interval 1−e−λt - Question 3 - Select One
If N0 is the number of radioactive nuclei initially present , then the number of nuclei remaining undecayed at the end of nth half life is
A2−nN0B2−nN0C2−nN0D2−nN0
The rate at which a particular decay process occurs in a radio sample, is proportional to the number of radio active nuclei present . If N is the number of radio active nuclei present at some instant, the rate of change of N is dNdt=−λN. Consider radioactive decay of A to B which may further decay either to X or to Y, λ1,λ2andλ3 are decay constants for A to B decay , B to X decay and B of Y decay respectively. if at t=0 number of nuclei of A,B , X and Y are N0,N0,zero and zero respectively
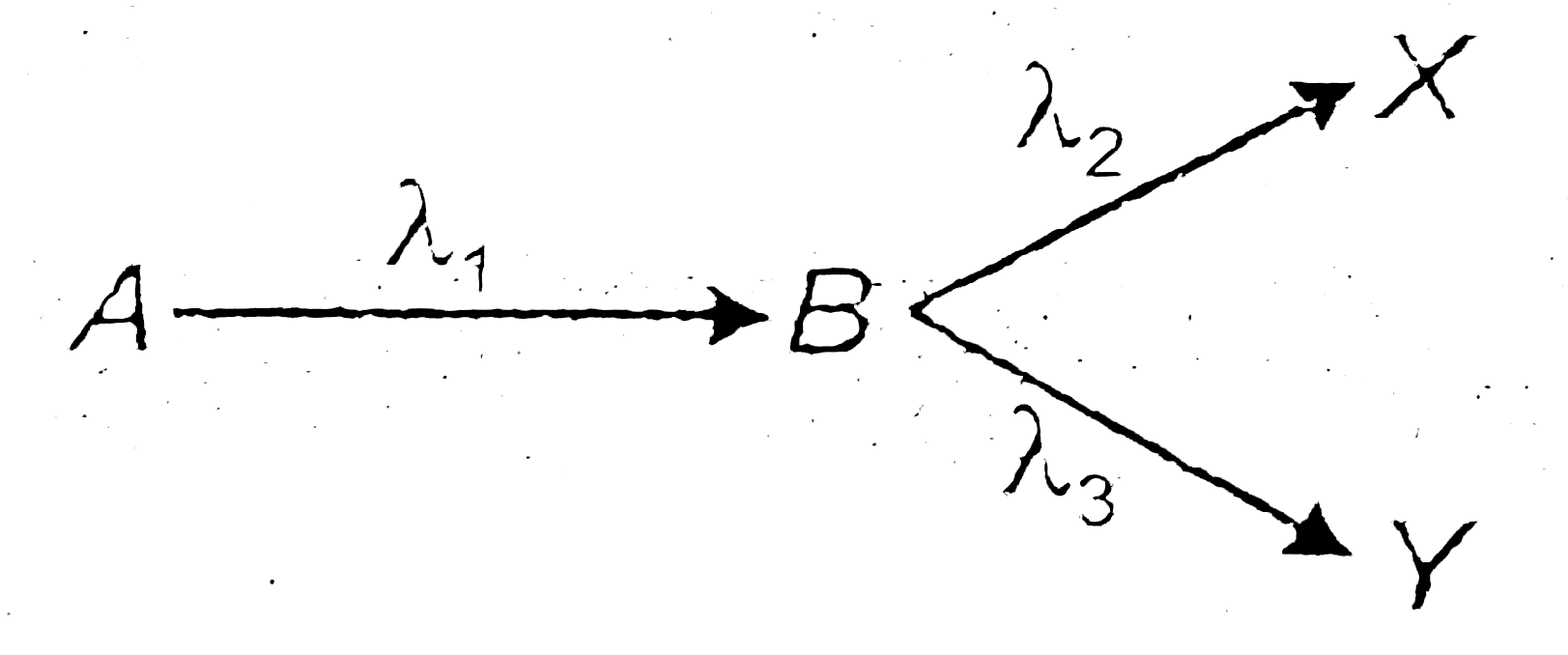
and N1,N2,N3,N4 are number of nuclei A,B , X and Y at any instant.
The number of nuclei of B will first increase then after a maximum value, it will decreases, ifView SolutionThe rate at which a particular decay process occurs in a radio sample, is proportional to the number of radio active nuclei present . If N is the number of radio active nuclei present at some instant, the rate of change of N is dNdt=−λN. Consider radioactive decay of A to B which may further decay either to X or to Y, λ1,λ2andλ3 are decay constants for A to B decay , B to X decay and B of Y decay respectively. if at t=0 number of nuclei of A,B , X and Y are N0,N0,zero and zero respectively

and N1,N2,N3,N4 are number of nuclei A,B , X and Y at any instant.
At t=∞, which of the following is incorrect ?View SolutionThe rate at which a particular decay process occurs in a radio sample, is proportional to the number of radio active nuclei present . If N is the number of radio active nuclei present at some instant, the rate of change of N is dNdt=−λN. Consider radioactive decay of A to B which may further decay either to X or to Y, λ1,λ2andλ3 are decay constants for A to B decay , B to X decay and B of Y decay respectively. if at t=0 number of nuclei of A,B , X and Y are N0,N0,zero and zero respectively

and N1,N2,N3,N4 are number of nuclei A,B , X and Y at any instant.
Rate of accumulation of B of any instant will beView SolutionShow that the decay rate R of a sample of radionuclide is related to the number of radioactive nuclei N at the same instant by the expression R=λN.
View SolutionSome nuclei of a radioactive material are undergoing radioactive decay. The time gap between the instances when a quarter of the nuclei have decayed and when half of the nuclei have decayed is given as :
(where λ is the decay constant)View Solution

