The free surface of oil in a tanker, at rest, is horizontal if the tanker starts ac celerating the free surface will be titled by an angle θ. If the ac celeration is a ms−2 what will be the slope of the free surface ?
To solve the problem of determining the slope of the free surface of oil in a tanker that is accelerating, we can follow these steps:
Step 1: Understand the Forces Acting on the Oil
When the tanker accelerates horizontally with an acceleration a, the oil inside experiences a pseudo force acting in the opposite direction of the acceleration. This pseudo force can be represented as Fpseudo=dm⋅a, where dm is the mass of an elemental volume of oil.
Step 2: Identify the Weight of the Oil
The weight of the elemental mass of oil is given by Fweight=dm⋅g, where g is the acceleration due to gravity.
Step 3: Resolve the Forces
When the tanker accelerates, the oil will tilt, and we can analyze the forces acting on an elemental mass dm of the oil. The forces acting on this mass can be resolved into two components:
- The component of the weight acting down the slope: Fweight,down=dm⋅g⋅sin(θ)
- The component of the pseudo force acting up the slope: Fpseudo,up=dm⋅a⋅cos(θ)
Step 4: Set Up the Equation
Since there is no relative motion along the inclined plane, we can set the forces equal to each other:
dm⋅g⋅sin(θ)=dm⋅a⋅cos(θ)
Step 5: Simplify the Equation
We can cancel dm from both sides of the equation (assuming dm≠0):
g⋅sin(θ)=a⋅cos(θ)
Step 6: Express tan(θ)
Dividing both sides by cos(θ) gives:
tan(θ)=ag
Final Result
Thus, the slope of the free surface of the oil in the tanker, represented by tan(θ), is given by:
tan(θ)=ag
When the tanker accelerates horizontally with an acceleration a, the oil inside experiences a pseudo force acting in the opposite direction of the acceleration. This pseudo force can be represented as Fpseudo=dm⋅a, where dm is the mass of an elemental volume of oil.
The weight of the elemental mass of oil is given by Fweight=dm⋅g, where g is the acceleration due to gravity.
When the tanker accelerates, the oil will tilt, and we can analyze the forces acting on an elemental mass dm of the oil. The forces acting on this mass can be resolved into two components:
- The component of the weight acting down the slope: Fweight,down=dm⋅g⋅sin(θ)
- The component of the pseudo force acting up the slope: Fpseudo,up=dm⋅a⋅cos(θ)
Since there is no relative motion along the inclined plane, we can set the forces equal to each other:
dm⋅g⋅sin(θ)=dm⋅a⋅cos(θ)
We can cancel dm from both sides of the equation (assuming dm≠0):
g⋅sin(θ)=a⋅cos(θ)
Dividing both sides by cos(θ) gives:
tan(θ)=ag
Thus, the slope of the free surface of the oil in the tanker, represented by tan(θ), is given by:
tan(θ)=ag
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Long Answer Type Questions3videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Very Short Answer Type Questions5videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Long answer Type Questions9videos
LAWS OF MOTION
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LONG SHORT ANSWER TYPE QUESTION16videos
MECHANICAL PROPERTIES OF SOLIDS
Similar Questions
A gas has no free surface.
View SolutionThe angle which the free surface of a liquid filled in a container will make with horizontal if the container is accelerated horizontally with acceleration g√3 is
View SolutionAbsorptive cells on free surface bear
View SolutionThe free surface of a liquid resting in an inertial frame is horizontal. Does the normal to the free surface pass through the centre of the earth? Think separately if the liquid is a. at te equaltor b. at a pole c. somewhere else.
View SolutionFree surfaces of long bones that form joints, sternal parts of ribs have
View SolutionWedge of 10kg is free to move on horizontal surface. At the given instant, acceleration of wedge is (string and pulleys are ideal)
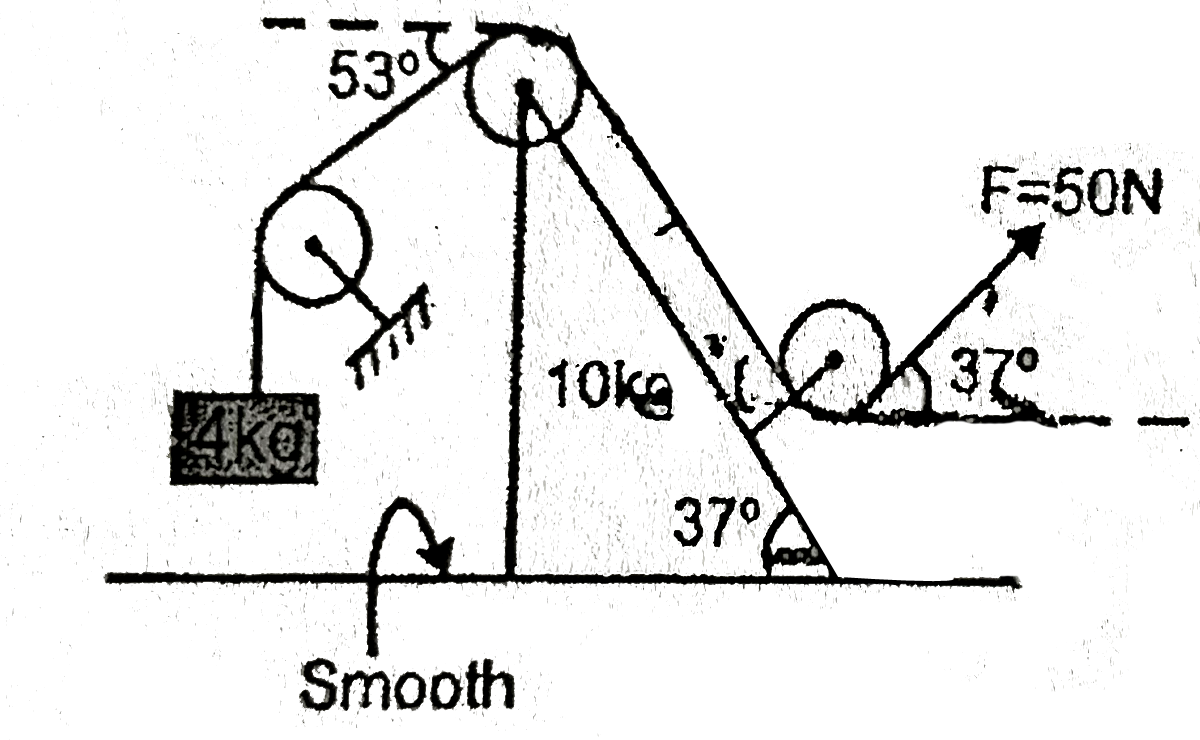 View Solution
View SolutionWhat is the fractional decrease in the value of free-fall acceleration g for a particle when it is lifted from the surface to an elevation h? (h<<R)
View SolutionA tank of height H is fully filled with water. If the water rushing from a hole made in the tank below the free surface , strikes the floor at a maximum horizontal distance , then the depth of the hole from the free surface must be
View SolutionEpithelial cells involved in absorption of digested food have on their free surface.
View SolutionEpithelial cells involved in absorption of digested food have on their free surface.
View Solution

