The friction coefficient between the two blocks shown in figure is $μ$ but the floor is smooth. A. What maximum horizontal force F can be applied without disturbing the equilibrium of the systme? b.suppose the horizontal force applied is double of that found in part a. Findthe accelerations of the two masses.

Video Solution

Text Solution

Verified by Experts

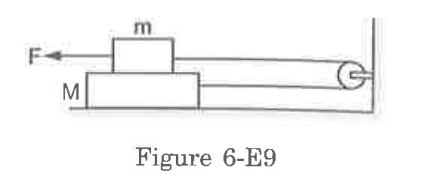
Both upper block andlower block will have acceleration $2 \frac{m}{s^{2}}$

$R_{1} = m g F = μ R_{1} - T = 0$
$\to T - μ R_{1} = 0$
$and$ F--mu mg =T $\dots . . i i < b r >$ rarr T=mu mg $< b r > P u \in g$ T=mu mg $< b r >$ F=mu mg +mu mg = 2mu mg $< b r > b .$ 2F=T-mumg -ma $< b r > = 0 ... ... ... i < b r >$ T-ma-mu mg =0 [:.R=mg] $< b r >$ rarr T=ma+mumg $< b r > P u \in g v a l u e o f T \in i . w e h a v e < b r >$ 2F-Mamu mg +mu mg-ma=0 $< b r > P u \in g$ F=2mumg $< b r > 2 (2 μ m g) - 2 μ m g = a (M + m)$
$\to 4 μ m g - 2 μ m g = a (M + m)$
$\to a = \frac{2 μ m g}{M + m}$
Both blocks move with this acceleration a in opposite direction.

Updated on:21/07/2023

|

Class 11 PHYSICS FRICTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Coefficient of static friction between the two blocks in Fig. 7.124 is $μ$ and the table is frictionless . Maximum horizontal force which can be applied on the lower such that the blocks move together , is :

A $μ m_{1} g$
B $μ m_{2} g$
C $μ (m_{1} - m_{2}) g$
D $μ (m_{1} + m_{2}) g$
The friction coefficient between the plank and floor is $μ$ . The man applies, the maximum possible force on the string and the system remains at rest. Then :

Afriction force between plank and surface is $\frac{2 μ m g}{1 + μ}$
Bfrictional force on man is zero
Ctension in the string is $\frac{2 μ m g}{1 + μ}$
Dnet force on man is zero
Each of the two block shown in the figure has mass m. The pulley is smooth and the coefficient of friction for all surfaces in contact is $μ$ . A constant horizontal force $P$ applied in two cases shown in such a way that block A start just sliding then the value of minimum force $P$ in case-I and case-II is :

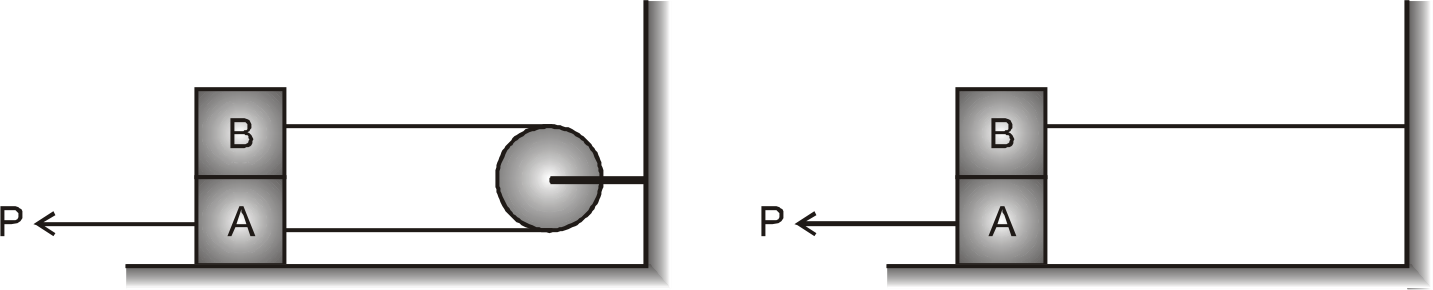A $2 μ m g, 3 μ m g$
B $3 μ m g, 2 μ m g$
C $4 μ m g, 3 μ m g$
D $3 μ m g, 3 μ m g$

HC VERMA-FRICTION-Exercises

Home
Ask Doubt
Profile