The graph showing the relation of the distance between two molecules with the inter molecular potential energy ( U ) is given in Figure. Find with the help of the graph.
(i) the distance between the molecule in their state of stable equilibrium.
(ii) the minimum and maximum distance between the molecules when the potential energy is −U1.
(iii) the energy required for the molecules to be free from each other when the distance between them is r2.
Text Solution
(i) The molecule are in stable equilibrium, when their potential energy is minimum . The distance corresponding to the minimum potential energy is r2.
(ii) The minimum distance corresponding to the P.Q. −U1 is r3 and the maximum distance corresponding to the potential energy −U1 is r1.
(iii) The energy required for the molecules to be free from eacth other when the distance between them is
r2=energy at infinite distance - energy at r=r2
=0−(U2)=U2
|
Topper's Solved these Questions
- PROPERTIES OF MATTERBook:ICSEChapter:PROPERTIES OF MATTERExercise:MODULE 1 (ELASTICITY)CONCEPTUAL SHORT ANSWER QUESTIONS WITH ANSWERS
Explore 12 Videos
- PROPERTIES OF MATTERBook:ICSEChapter:PROPERTIES OF MATTERExercise:MODULE 1 (ELASTICITY)LONG ANSWER QUESTIONS
Explore 5 Videos
- PROPERTIES OF MATTERBook:ICSEChapter:PROPERTIES OF MATTERExercise:MODULE 4 (SOLVED EXAMPLES)
Explore 11 Videos
- OSCILLATIONS Book:ICSEChapter:OSCILLATIONS Exercise:SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)
Explore 2 Videos
- SAMPLE QUESTION PAPER - 01 Book:ICSEChapter:SAMPLE QUESTION PAPER - 01 Exercise:SECTION - D
Explore 12 Videos
Similar Questions
Knowledge Check
The graph between potential energy U and displacement X in the state of stable equilibrium will be–
A B
B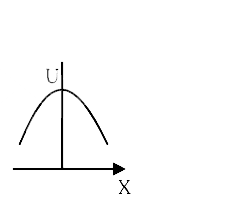 C
C D
D
In a DNA molecule distance between two bases is
A2nm/20ÅB0⋅2nm/2ÅC3⋅4nm/34ÅD0⋅34nm/3⋅4ÅIf typical size of a gas molecule is 2Å, average distance between the molecules is
A1ÅB2ÅC<20ÅD≥20Å
If the potential energy between two molecules is given by U=−Ar6+Br12 , then at equilibrium , separation between molecules , and the potential energy are :
View SolutionThe potential energy curve for the H2 molecule as a function of internuclear distance is :
View SolutionThe potential energy curve for the H2 molecule as a function of internuclear distance is :
View SolutionThe relation between conservative force and potential energy U is given by :–
View SolutionAssertion : On decreasing the distance between two masses potential energy increases.
Reason : Potential energy U=GMmr.
View Solution
