The graph shows the behaviour of a steel wire in the region for whoch the wire obeys Hooke's law. The graph is a parabola. The variables X and Y -axes, respectively can be [ stress (σ),strain (ε) and elastic potential energy(U) ]
![The graph shows the behaviour of a steel wire in the region for whoch the wire obeys Hooke's law. The graph is a parabola. The variables X and Y -axes, respectively can be [ stress (sigma),strain ( epsilon) and elastic potential energy(U) ]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/DCP_VO2_C15_EO1_026_Q01.png)
A) U,σ
B) U,ε
C) σ,ε
D) None of these
The correct Answer is:B
U=12σε=12(Yε)ε
⇒U=12Yε2 is similar to x =ky2
Which is a parabola passing through origin and symmetric about x-axis.
Topper's Solved these Questions
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Level 1 Subjective
8 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Level 2 Single Correct
10 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Assertion And Reason
22 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
469 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer
17 Videos
Similar Questions
The graph show the behaviour of a length of wire in the region for which the substances obeys Hooke's law. P and Q represent
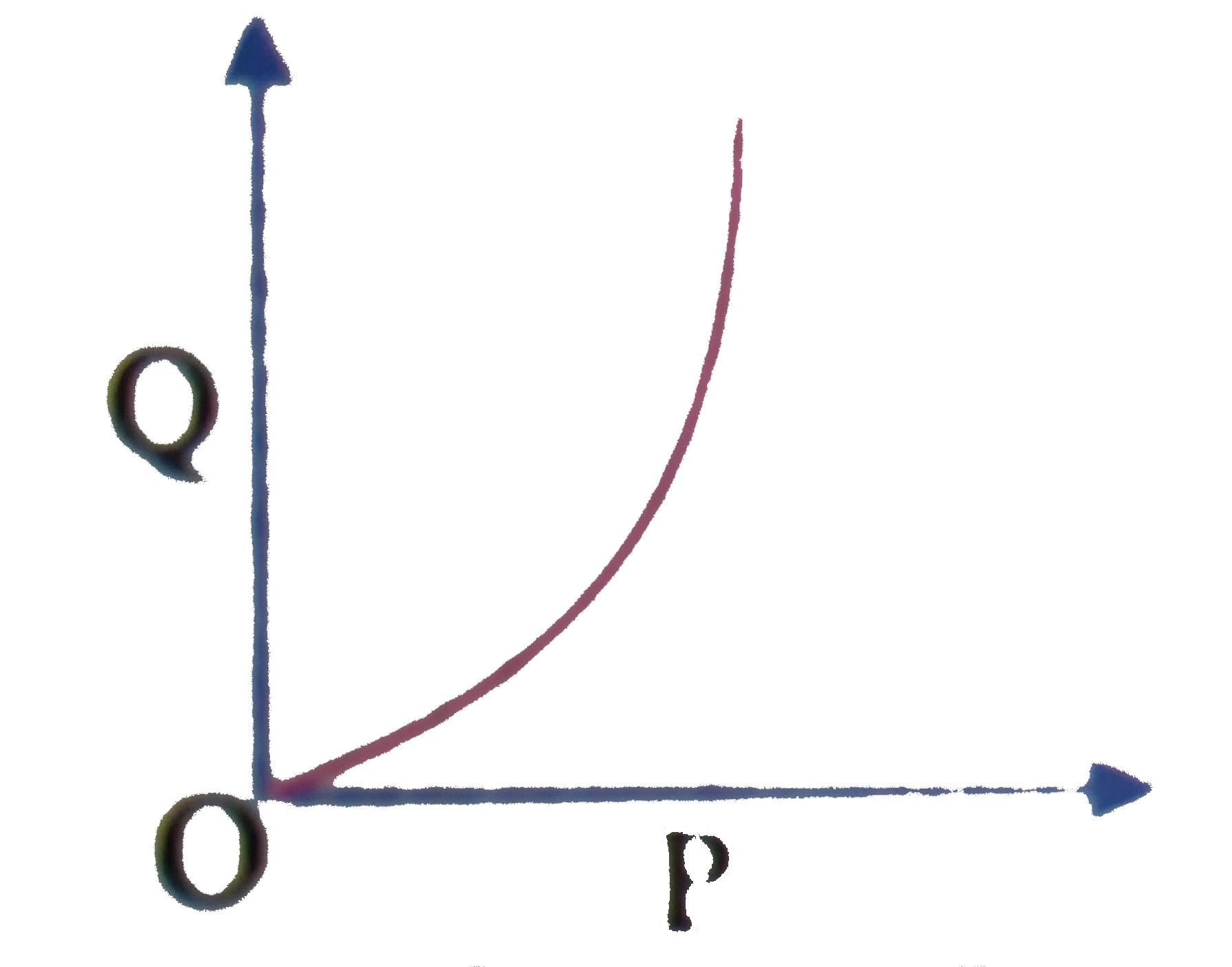
View Solution(i) State Hook's law.
(ii) Draw a labelled graph of tensile stress against tensile strain for a metal wire upto the breaking point. Shhow on your graph the region in which Hooke's law is obeyed.
What is the significance of the area between the graph and the strain axis withing the Hooke's law region?
View Solution
Knowledge Check
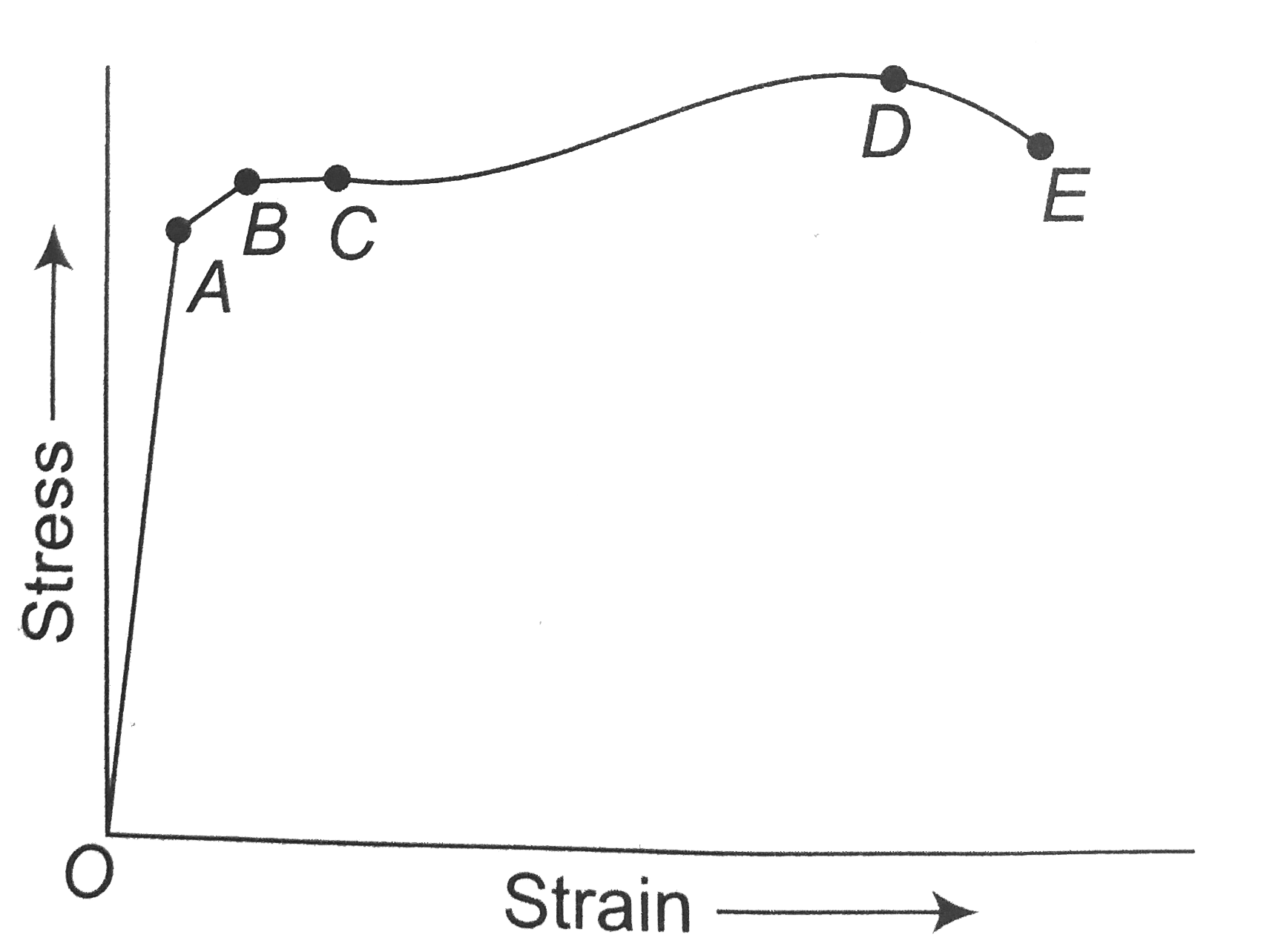
The stress strain graph for a metal wire is as shown in the figure. In the graph, the region in which Hooke's law is obeyed, the ultimate strength and fracture are represented byAOA, C, DBOB, D, ECÂ OA, D, EDOB, C, D
When a uniform metallic wire is stretched the lateral strain produced in it is β .if σ and Y are the Poisson's ratio and Young's modulus for wire, then elastic potential energy density of Wire is
View SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.
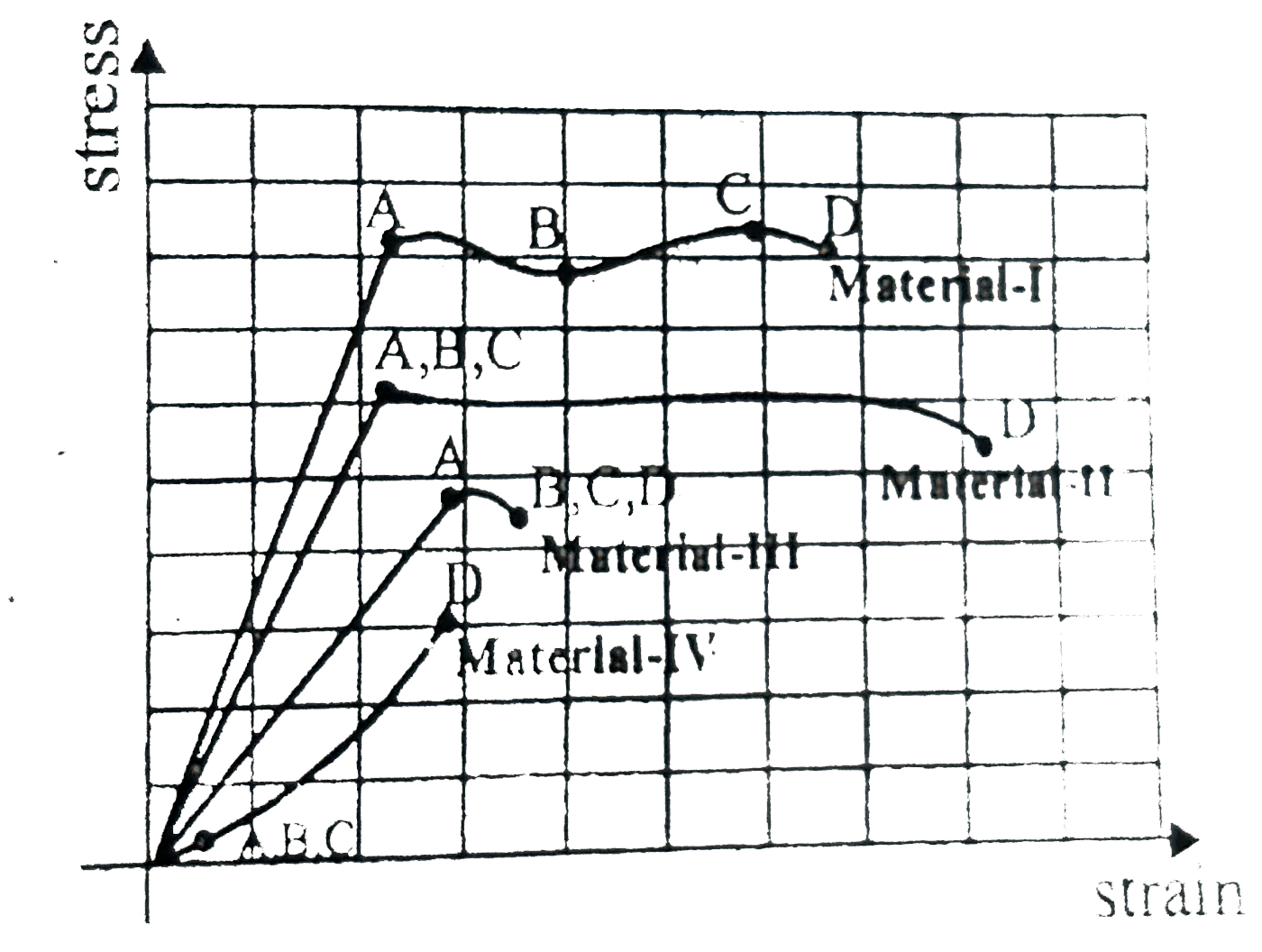
Material which is good for making wires by stretching is
View SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.
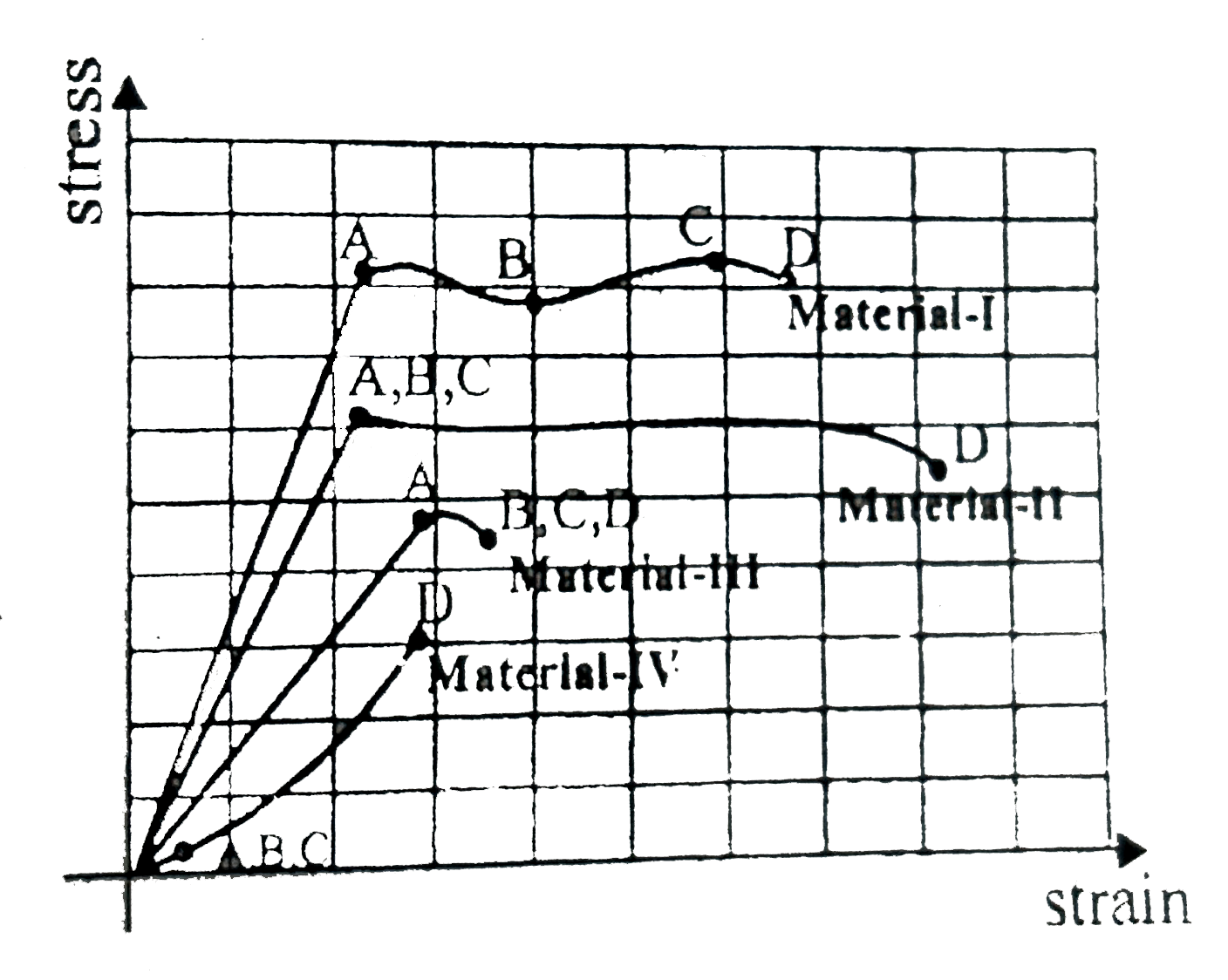
If you bough a new shoe which bites in the beginning and later on fits perfectly, then the material used to making the shoe is
View SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.

If you bough a new shoe which bites in the beginning and later on fits perfectly, then the material used to making the shoe is
View SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.

If you bough a new shoe which bites in the beginning and later on fits perfectly, then the material used to making the shoe is
View SolutionThe stress strain graph for a metal wire is shown in the fig. Up to the point E, the wire returns to its original state O along the curve EPO, when it is gradually unloaded. Point B corresponds to the fracture of the wire.
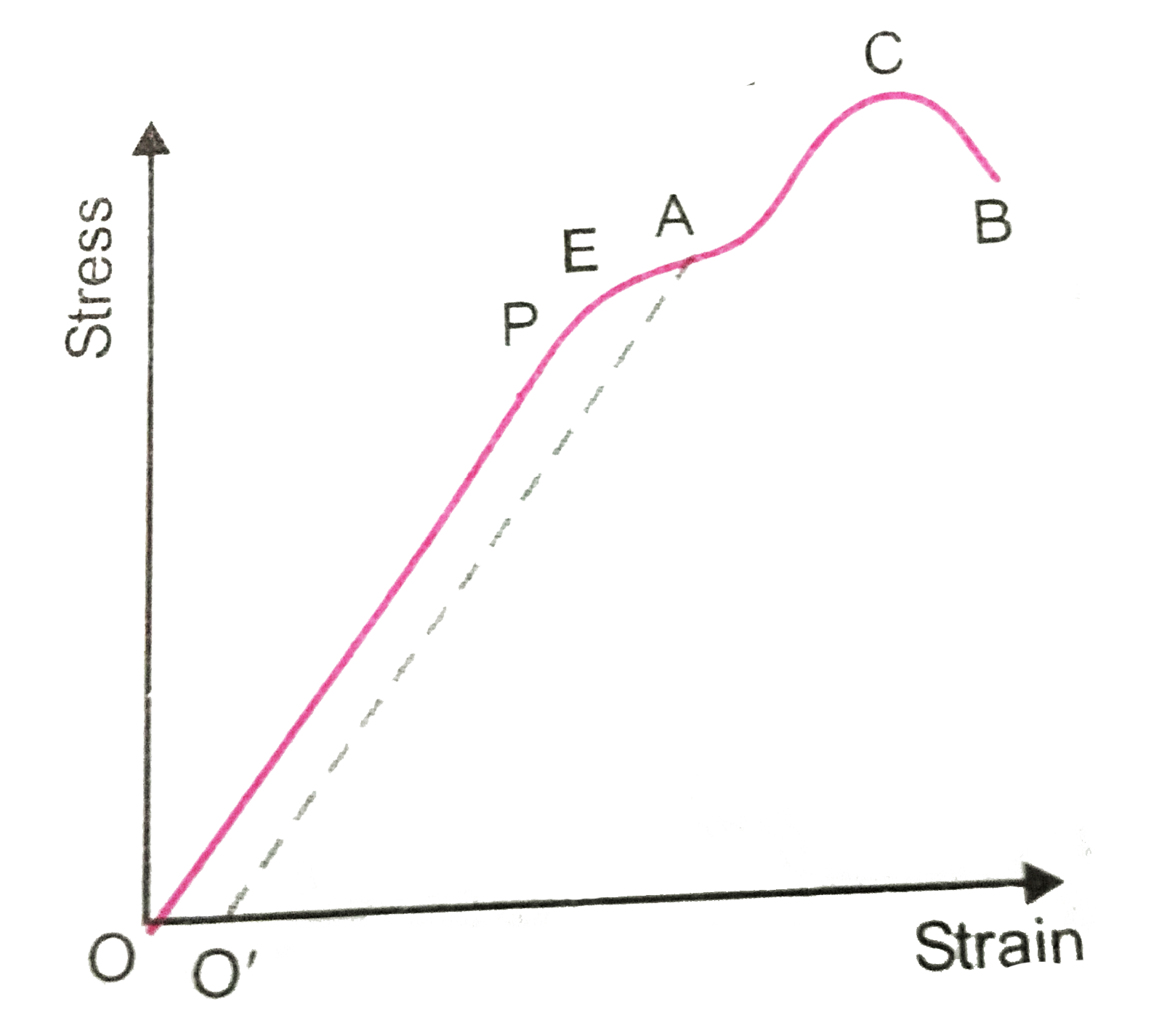
(a) Up to what point on the curve is Hooke's law obeyed? (this point some times called proportional limits).
(b) Which point on the curve corresponding to elastic limit or yield point of the wire?
(c ) Indicate the elastic and plastic regions of the stress-strain graph.
(d) Describe what happens when the wire is loaded up to a stress corresponding to the point A on the graph and then unloaded gradually. In particular explain the dotted curve.
(e) What is peculiar about the portion of the stress- strain graph from C to B? Up to what stress can the wire be subjected without causing fracture?
View SolutionAccording to Hooke's law, within the elastic limit stress/strain = constant. This constant depends on the type of strain or the type of force acting. Tensile stress might result in compressional or elongative strain, however, a tangential stress can only cause a shearing strain. After crossing the elastic limit, the material undergoes elongation and beyond a stage beaks. All modulus of elasticity are basically constants for the materials under stress.
If stress/strain is x in elastic region and y in the region of yield, then
View Solution
