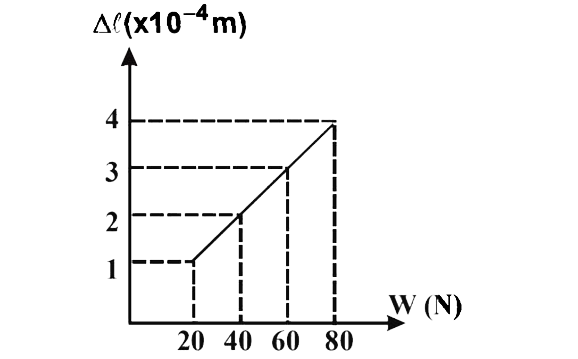
The graph shows the extension (Δl) of a wire of length 1m suspended from the top of a roof at one end with a load W connected to other end if the cross sectional area of wire is 10−6m2, calculate the young's modulus of the material of the wire.Solution in Tamil
When W=20N,Δl=1×10−4m,A=10−6

∴y=FA.lΔl=WA.(l)Δl=2010−6×11×10−4
=2×1011Nm−2
Topper's Solved these Questions
- BOOK - SURA PUBLICATIONCHAPTER - PROPERTIES OF MATTEREXERCISE - Value based Questions5videos
PROPERTIES OF MATTER
- BOOK - SURA PUBLICATIONCHAPTER - PROPERTIES OF MATTEREXERCISE - Numerical Problems13videos
PROPERTIES OF MATTER
- BOOK - SURA PUBLICATIONCHAPTER - OSCILLATIONSEXERCISE - VALUE BASED QUESTIONS2videos
OSCILLATIONS
- BOOK - SURA PUBLICATIONCHAPTER - PUBLIC EXAM QUESTION PAPER MARCH-2019EXERCISE - Part-IV10videos
PUBLIC EXAM QUESTION PAPER MARCH-2019
Similar Questions
the r.m.s. velocity of the molecules of a certain diatomic gas is found to be 1.6 Km/sec. the gas is
02:06View SolutionThe poisson ratio of a material is 0.5 if a force is applied to a wire of this material, there is a decrease in the cross sectional area by 4% what is the percentage increases in the length.
02:53View SolutionStudent in a class were asked by their science teacher about different types of motion , with Examples. But few students were confused with explanation ,for example . Periodic motion. SHM , Oscillatory motion , Rotational motion. SHM , Oscillatory motion . Periodic motion, etc. How would have the teacher explained , so the students understood easily ?
(i) What are path difference & phase difference ?
(ii) For the waves , given below find out the phase & path differences.
 01:45View Solution
01:45View SolutionThe force F acting on a body moving in a circular path depends on mass of the body (m) velocity(v) and radius (r) of the circular path. Obtain the expression for the force by dimensional analysis method (k=1)
03:53View SolutionThe adjacent graph shows the estension (Δl) of a wire of length 1m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross-sectional area of the wire is 10−6m2, calculate the Young's modulus of the material of the wire.
 02:47View Solution
02:47View SolutionThe graph shows the extension of a wire of length 1m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross sectional area of the wire is 1mm^(2) , then the young's modulus of the material of the wire is (a). 2xx10^(11)Nm^(-2) (b). 2xx10^(10)Nm^(-2) (c). (1)/(2)xx10^(11)Nm^(-2) (d). none of these
03:16View SolutionThe adjacent graph shows the extension Deltal of a wire of length 1m, suspended from the f top of a roof at one end and with a loaf w connected to the other end. If the cross-sectional area of the wire is 10^(6) m^(2) calculate the young's modulus of the material of the wire .
02:16View SolutionThe graph shown the extension of is wire of length 1 m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross sectional area of the wire is 1 mm^(2) , then the Young's modulus of the material of the wire. ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_RACE_R64_E01_001_Q01.png" width="80%"gt
View SolutionOne end of a uniform wire of length l and weight W is attached to a point in the roof and a weight W/2 is suspended from the lower end. If A is the area fo cross-section of the wire, then stress of the wire at its midpoint will be
View SolutionA wire of length 1 m and area of cross section 2xx10^(-6)m^(2) is suspended from the top of a roof at one end and a load of 20 N is applied at the other end. If the length of the wire is increased by 0.5xx10^(-4)m , calculate its Young’s modulus (in 10^(11)N//m^(2)) .
01:54View SolutionThe adjacent graph shows the extension (DeltaI) of a wire of length 1 m suspended from the top of a roof at one end with a load W connected to the other end. If the cross-sectional area of the wire is 10^(-6) m ^(2), calculate The Young's modulus of the material of the wire is ........
03:37View SolutionOne end of a uniform wire of length l and weight W is attached to a point in the roof and weight W /2 is suspended from the lower end. If A is the area of cross section of the wire then stress in the wire at its mid point is
02:30View SolutionOne end of a uniform wire of length l and weight W is attached to a point in the roof and weight W /2 is suspended from the lower end. If A is the area of cross section of the wire then stress in the wire at its mid point is
02:27View SolutionThe adjacent graph shows the extension Δl of a wire of length 1m, suspended from the f top of a roof at one end and with a loaf w connected to the other end. If the cross-sectional area of the wire is 106m2 calculate the young's modulus of the material of the wire .
 02:20View Solution
02:20View SolutionThe adjacent graph shows the estension (Deltal) of a wire of length 1m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross-sectional area of the wire is 10^-6m^2 , calculate the Young's modulus of the material of the wire.
02:59View Solution

