A wire of length 1 m and area of cross section 2×10−6m2 is suspended from the top of a roof at one end and a load of 20 N is applied at the other end. If the length of the wire is increased by 0.5×10−4m, calculate its Young’s modulus (in 1011N/m2).
The correct Answer is:2
To calculate Young's modulus for the given wire, we will use the formula:
Y=F⋅LΔL⋅A
Where:
- Y = Young's modulus
- F = applied force (load)
- L = original length of the wire
- ΔL = change in length of the wire
- A = area of cross-section of the wire
Step 1: Identify the given values
- Length of the wire, L=1m
- Area of cross-section, A=2×10−6m2
- Load applied, F=20N
- Increase in length, ΔL=0.5×10−4m
Step 2: Substitute the values into the Young's modulus formula
Now, substituting the values into the formula:
Y=20N⋅1m0.5×10−4m⋅2×10−6m2
Step 3: Calculate the denominator
First, calculate the denominator:
ΔL⋅A=0.5×10−4m⋅2×10−6m2=1×10−10m3
Step 4: Substitute and simplify
Now substitute this back into the equation for Y:
Y=20N1×10−10m3
Y=20×1010N/m2
Step 5: Convert to the required units
To express Y in terms of 1011N/m2:
Y=2×1011N/m2
Final Answer
Thus, the Young's modulus of the wire is:
Y=2×1011N/m2
- Y = Young's modulus
- F = applied force (load)
- L = original length of the wire
- ΔL = change in length of the wire
- A = area of cross-section of the wire
- Length of the wire, L=1m
- Area of cross-section, A=2×10−6m2
- Load applied, F=20N
- Increase in length, ΔL=0.5×10−4m
Now, substituting the values into the formula:
First, calculate the denominator:
Now substitute this back into the equation for Y:
To express Y in terms of 1011N/m2:
Thus, the Young's modulus of the wire is:
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Level -2
50 Videos
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Main (Archive) Level - 1
48 Videos
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced (Archive) Level - 2 (MATRIX MATCH TYPE)
1 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IN-CHAPTER EXERCISE-K
10 Videos
- QUIZBOOK - VMC MODULES ENGLISHCHAPTER - QUIZEXERCISE - PHYSICS
30 Videos
Similar Questions
The adjacent graph shows the extra extension (Δx) of a wire of length 1m suspended from the top of a roof at one end with an extera load Δw connected to the other end If the cross sectional area of the wire is 10−5m2 calculate the Young's modulus of the meterial of the wire
(A) 2×1011N/m2 (B) 2×10−11N/m2 (c) 3×10913)N/m3 (D) 2×1016N/m2
 .
.
View SolutionThe adjacent graph shows the estension (Δl) of a wire of length 1m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross-sectional area of the wire is 10−6m2, calculate the Young's modulus of the material of the wire.
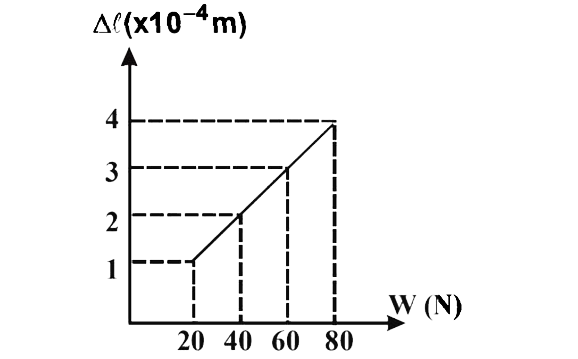
View Solution
Knowledge Check
The adjacent graph shows the extension Δl of a wire of length 1m, suspended from the f top of a roof at one end and with a loaf w connected to the other end. If the cross-sectional area of the wire is 106m2 calculate the young's modulus of the material of the wire .
 A2×1011N/m2B2×10−11N/m2C3×10−12N/m2D2x10−13N/m2
A2×1011N/m2B2×10−11N/m2C3×10−12N/m2D2x10−13N/m2
_S01_065_Q01.png)
The graph shows the extension of a wire of length 1m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross sectional area of the wire is 1mm2, then the young's modulus of the material of the wire is
(a). 2×1011Nm−2
(b). 2×1010Nm−2
(c). 12×1011Nm−2
(d). none of these
View SolutionThe adjacent graph shows the extension Δl of a wire of length 1m, suspended from the f top of a roof at one end and with a loaf w connected to the other end. If the cross-sectional area of the wire is 106m2 calculate the young's modulus of the material of the wire .

View SolutionThe graph shown the extension of is wire of length 1 m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross sectional area of the wire is 1mm2, then the Young's modulus of the material of the wire.

View Solution_E01_080_Q01.png)
A copper wire of length 3 m and area of cross-section 1mm2 passes through an arrangement of two friction-less pulleys P1 and P2. One end of the wire is rigidly clamped and a mass of 1 kg is hanged from the other end if the young's modulus for copper is 10×1010N/m2 , then the elongation in the wire is
View SolutionA force of 200 N is applied at one end of a wire of length 2m and having area of cross-section 10−2cm2. The other end of the wire is rigidly fixed. If coefficient of linear expansion of the wire α=8×10−6/.∘C and Young's modulus Y=2.2×1011N/m2 and its temperature is increased by 5∘C, then the increase in the tension of the wire will be
View SolutionWhat force is required to stretch a steel wire to double its length when its area of cross section 1 cm2 and Young.s modulus 2×1011N/m2.
View SolutionA wire 4 m long and cross section 3×10−6m2is stretched by Imm. If its Young.s modulus is 2×1011N/m2, find the energy stored in the wire.
View Solution
