The graph that represents variation of g with depth (d) from the surface of the earth is
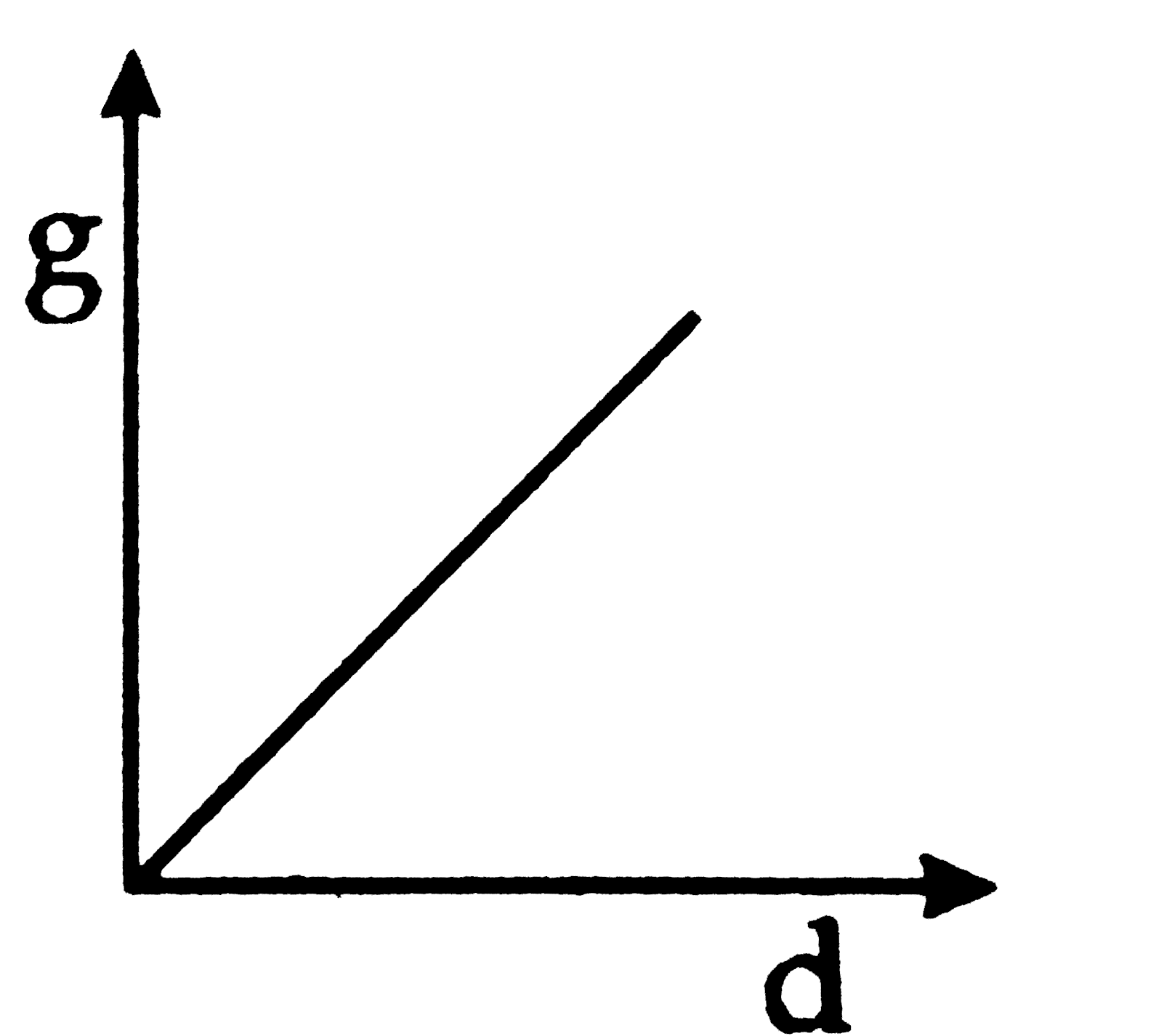
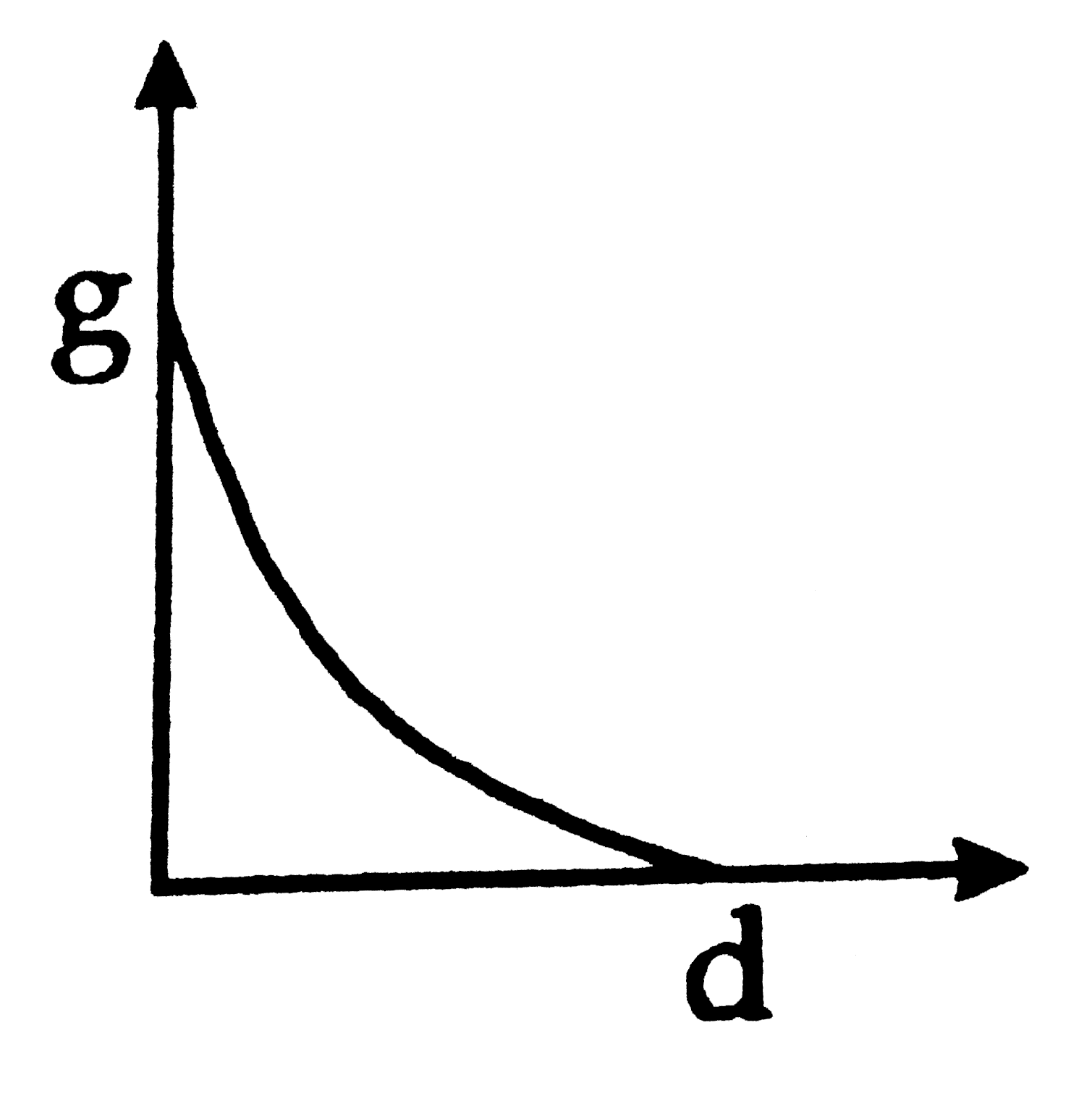

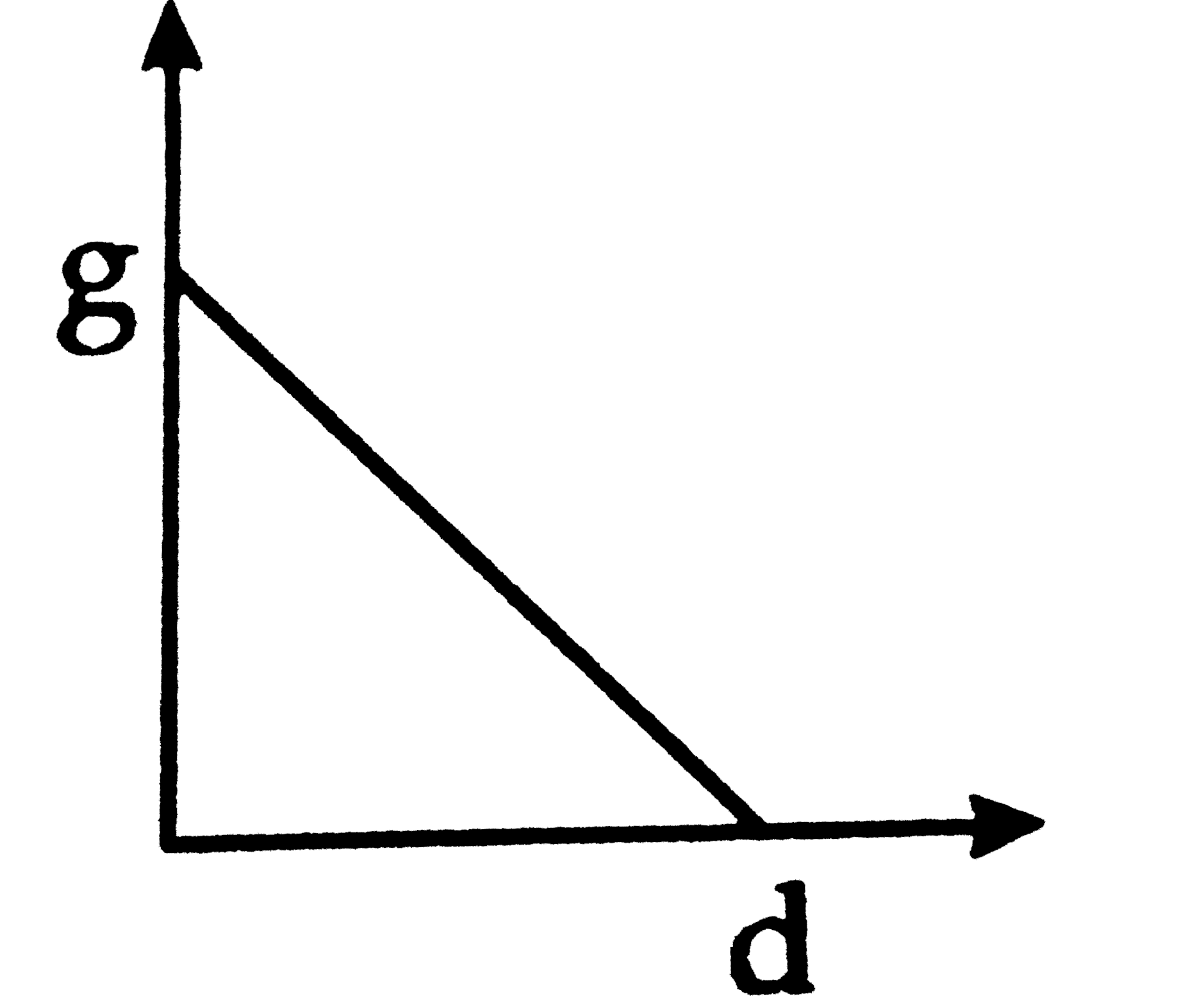
The correct Answer is:d
To determine the graph that represents the variation of gravitational acceleration g with depth d from the surface of the Earth, we can follow these steps:
Step 1: Understand the relationship between g and depth d
The acceleration due to gravity g at a depth d inside the Earth can be expressed using the formula:
g′=g−gdR
where:
- g′ is the acceleration due to gravity at depth d,
- g is the acceleration due to gravity at the surface of the Earth,
- R is the radius of the Earth.
Step 2: Analyze the formula
From the formula, we can see that as d increases (i.e., as we go deeper into the Earth), the term gdR increases. This means that g′ decreases as d increases.
Step 3: Determine the behavior of g′
- At d=0 (the surface), g′=g.
- As d increases towards the center of the Earth, g′ decreases linearly because the term gdR increases linearly with d.
Step 4: Sketch the graph
The graph of g′ versus d will start at g when d=0 and will decrease linearly as d increases. Therefore, the graph will be a straight line that slopes downwards.
Step 5: Conclusion
The correct representation of the variation of g with depth d is a straight line that starts from g at d=0 and decreases linearly as d increases.
- g′ is the acceleration due to gravity at depth d,
- g is the acceleration due to gravity at the surface of the Earth,
- R is the radius of the Earth.
- As d increases towards the center of the Earth, g′ decreases linearly because the term gdR increases linearly with d.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The graph that represents variation of g with height (h) from the surface of the earth is
A B
B C
C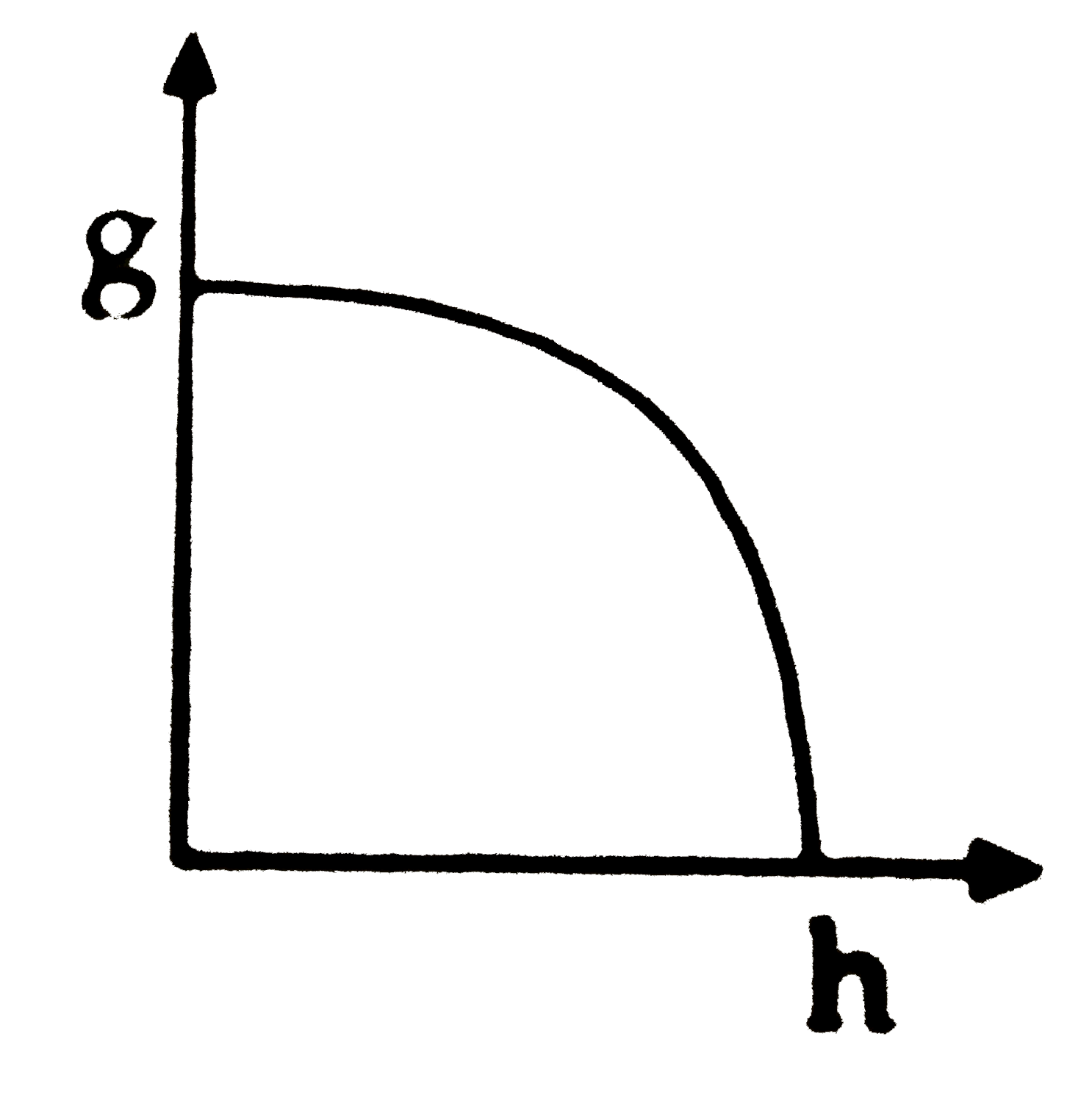 D
D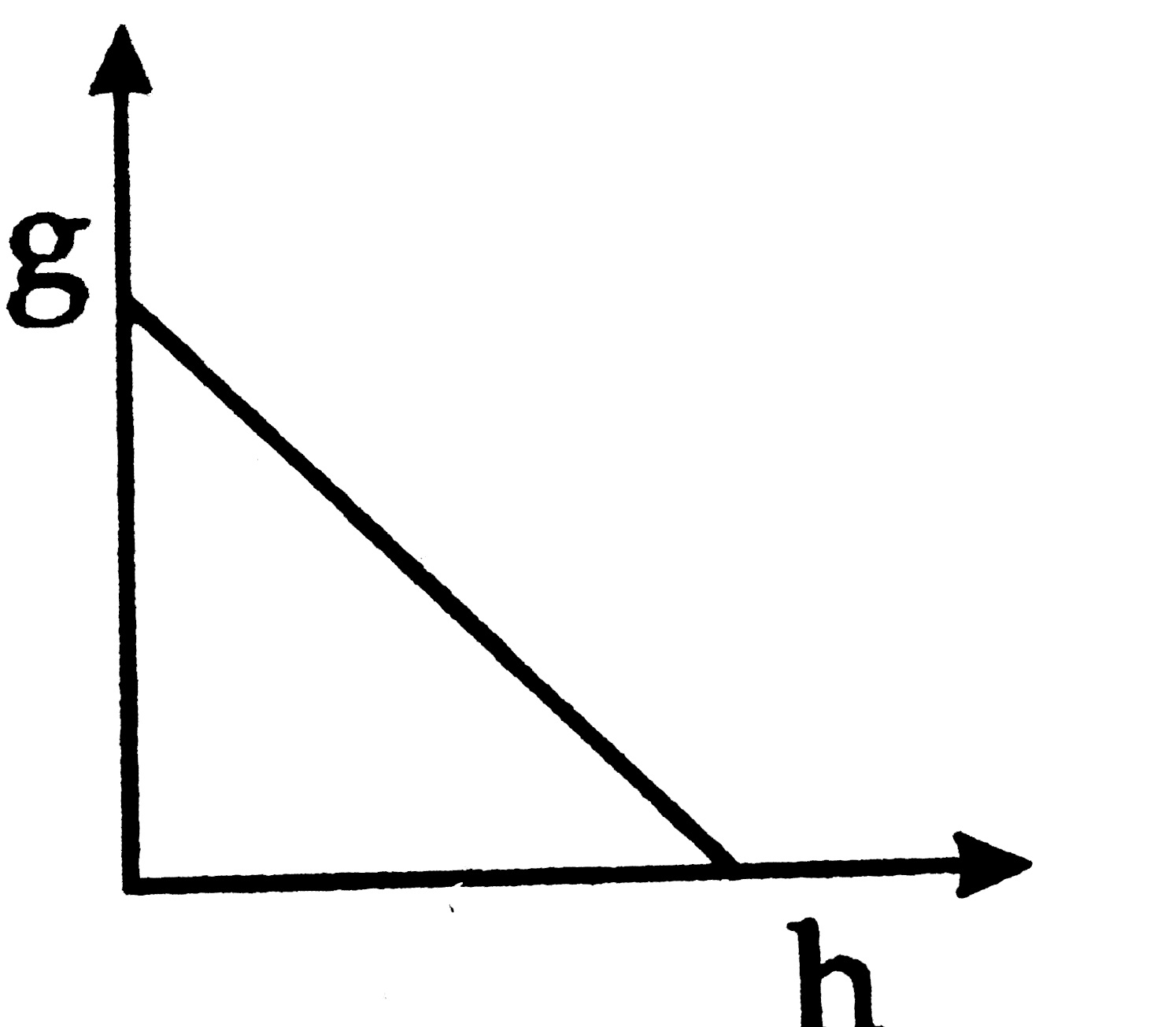
The graph that represents variation of g at the equator with square of angular velocity of rotation of earth is
A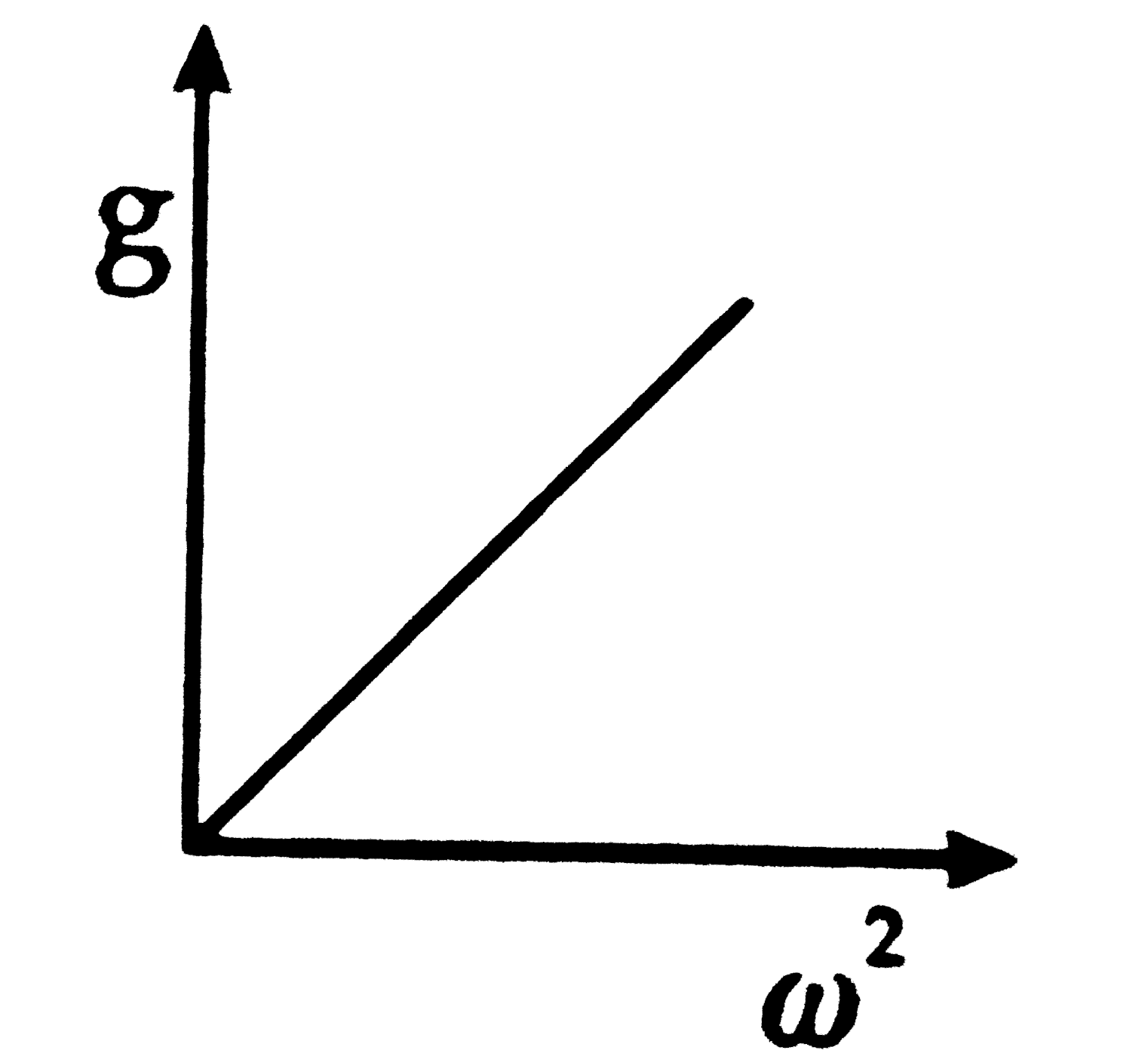 B
B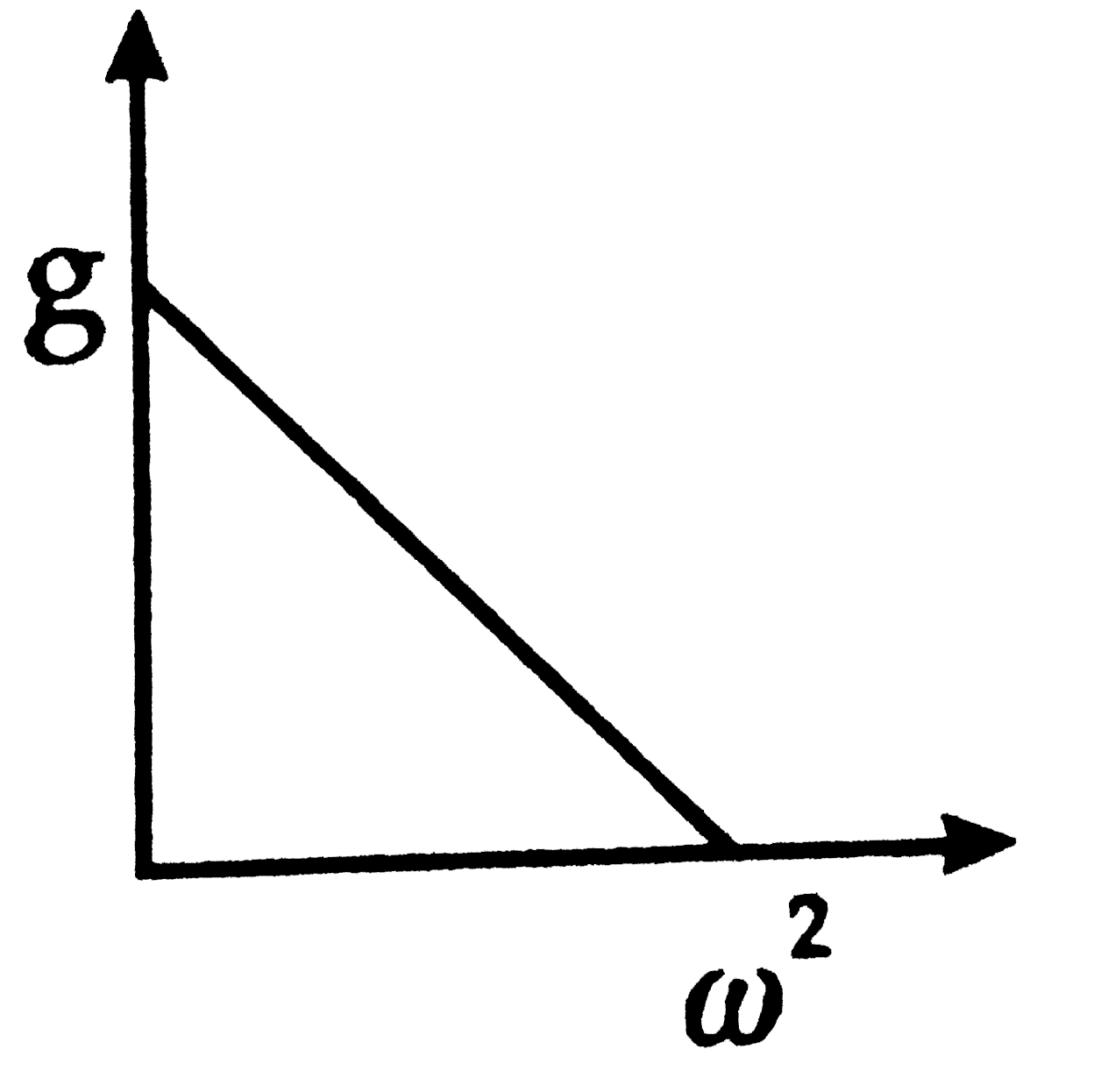 C
C D
D
Which of the following graphs shows the variation of acceleration due to gravity g with depth h from the surface of the earth ?
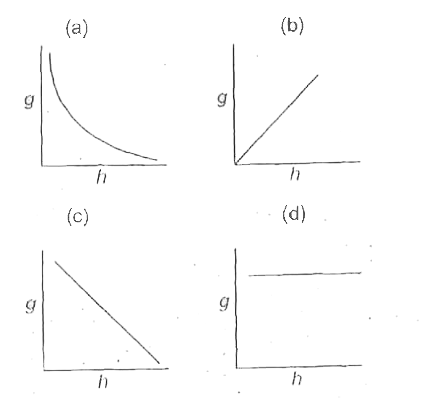 A(a)B(b)C(c )D(d)
A(a)B(b)C(c )D(d)
The acceleration due to gravity at a depth R/2 below the surface of the earth is
View Solutiona. Find the height from the earth's surface where g will be 25% of its value on the surface of earth (R=6400km). b. Find the percentage increase in the value of g at a depth h from the surface of earth.
View SolutionThe value of the acceleration due to gravity is g1 at a height h=(R)/(2)(R= radius of the earth) from the surface of the earth.It is again equal to (g1/2) at a depth d below the surface of the earth.The ratio d/R equals:
View SolutionThe value of the acceleration due to gravity is g1 at a height h=R2 (R=radius of the earth) from the surface of the earth.It is equal to 2g1 at a depth d below the surface of the earth.The ratio (dR) is equal to:
View SolutionThe acceleration due to gravity at a depth d below the surface of the earth is 20% of its value at the surface. What is the value of d if the radius of the earth=6400km ?
View Solution
