The instantaneous displacement x of a particle executing simple harmonic motion is given by x=a1sinωt+a2cos(ωt+π6). The amplitude A of oscillation is given by
√a21+a22+2a1a2cos(π6)
√a21+a22+2a1a2cos(π3)
√a21+a22−2a1a2cos(π6)
√a21+a22−2a1a2cos(π3)
The correct Answer is:D
To find the amplitude A of the oscillation given the instantaneous displacement x of a particle executing simple harmonic motion as
x=A1sin(ωt)+A2cos(ωt+π6),
we can follow these steps:
Step 1: Rewrite the cosine term
First, we can rewrite the cosine term using the angle addition formula:
cos(ωt+π6)=cos(ωt)cos(π6)−sin(ωt)sin(π6).
Substituting the values of cos(π6)=√32 and sin(π6)=12, we get:
cos(ωt+π6)=√32cos(ωt)−12sin(ωt).
Step 2: Substitute back into the equation
Now substituting this back into the original equation for x:
x=A1sin(ωt)+A2(√32cos(ωt)−12sin(ωt)).
This simplifies to:
x=(A1−A22)sin(ωt)+√32A2cos(ωt).
Step 3: Identify coefficients
Let:
B=A1−A22(coefficient of sin(ωt))
C=√32A2(coefficient of cos(ωt)).
Step 4: Calculate the amplitude
The amplitude A of the oscillation can be found using the formula:
A=√B2+C2.
Substituting the values of B and C:
A=
⎷(A1−A22)2+(√32A2)2.
Step 5: Simplify the expression
Now we can simplify this expression:
A=√(A1−A22)2+34A22.
Final Result
Thus, the amplitude A of the oscillation is given by:
A=√(A1−A22)2+34A22.
First, we can rewrite the cosine term using the angle addition formula:
Now substituting this back into the original equation for x:
Let:
C=√32A2(coefficient of cos(ωt)).
The amplitude A of the oscillation can be found using the formula:
⎷(A1−A22)2+(√32A2)2.
Now we can simplify this expression:
Thus, the amplitude A of the oscillation is given by:
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
Knowledge Check
The displacement of a particle executing simple harmonic motion is given by y=4sin(2t+ϕ). The period of oscillation is
A2/πBπ/2CπD2πThe displacement of a particle executing simple harmonic motion is given by
x=3sin(2πt+π4)
where x is in metres and t is in seconds. The amplitude and maximum speed of the particle isA3m, 2πms−1B3m, 4πms−1C3m, 6πms−1D3m, 8πms−1
The amplitude of given simple harmonic motion is y=(3sinωt+4cosωt)m
View SolutionThe total energy of a particle having a displacement x, executing simple harmonic motion is
View SolutionThe displacement of a particle performing simple harmonic motion is given by, x=8sinωt + 6 cos ωt, where distance is in cm and time is in second. What is the amplitude of motion?
View SolutionA particle executing simple harmonic motion of amplitude 5 cm has maximum speed of 31.4 cm / s . The frequency of its oscillation is
View SolutionThe plot of velocity (v) versus displacement (x) of a particle executing simple harmonic motion is shown in figure. The time period of oscillation of particle is :-

View SolutionThe acceleration-displacement graph of a particle executing simple harmonic motion is shown in the figure. The frequency of oscillation is
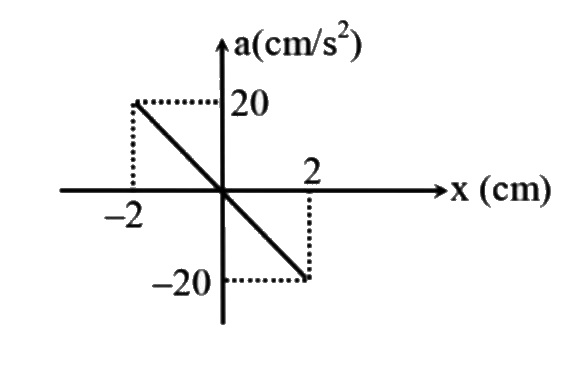
View Solution
