The intensity level of two sounds are 100 dB and 50 dB. What is the ratio of their intensities?
101
103
105
1010
The correct Answer is:C
To find the ratio of the intensities of two sounds with intensity levels of 100 dB and 50 dB, we can follow these steps:
Step 1: Understand the formula for intensity level
The intensity level B in decibels (dB) is given by the formula:
B=10log10(II0)
where I is the intensity of the sound and I0 is the reference intensity.
Step 2: Set up the equations for both sounds
Let B1 be the intensity level of the first sound (100 dB) and B2 be the intensity level of the second sound (50 dB). We can write:
B1=10log10(I1I0)(for 100 dB)
B2=10log10(I2I0)(for 50 dB)
Step 3: Substitute the values of B1 and B2
Substituting the values:
100=10log10(I1I0)
50=10log10(I2I0)
Step 4: Simplify the equations
Dividing both equations by 10 gives:
10=log10(I1I0)
5=log10(I2I0)
Step 5: Convert logarithmic form to exponential form
Converting from logarithmic to exponential form:
I1I0=1010
I2I0=105
Step 6: Find the ratio of the intensities
Now, we can find the ratio of the intensities I1I2:
I1I2=I1I0I2I0=1010105=1010−5=105
Conclusion
Thus, the ratio of the intensities I1 to I2 is:
I1I2=105
The intensity level B in decibels (dB) is given by the formula:
B=10log10(II0)
where I is the intensity of the sound and I0 is the reference intensity.
Let B1 be the intensity level of the first sound (100 dB) and B2 be the intensity level of the second sound (50 dB). We can write:
B1=10log10(I1I0)(for 100 dB)
B2=10log10(I2I0)(for 50 dB)
Substituting the values:
100=10log10(I1I0)
50=10log10(I2I0)
Dividing both equations by 10 gives:
10=log10(I1I0)
5=log10(I2I0)
Converting from logarithmic to exponential form:
I1I0=1010
I2I0=105
Now, we can find the ratio of the intensities I1I2:
I1I2=I1I0I2I0=1010105=1010−5=105
Thus, the ratio of the intensities I1 to I2 is:
I1I2=105
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Multiple Correct44videos
SOUND WAVES AND DOPPLER EFFECT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Assertion-Reasoning24videos
SOUND WAVES AND DOPPLER EFFECT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Subjective56videos
SOUND WAVES AND DOPPLER EFFECT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Comprehension Type5videos
SUPERPOSITION AND STANDING WAVES
Similar Questions
Two sound waves from two different sources interfere at a point to yield a sound of varying intensity. The intensity level between the maximum and minimum is 20 dB. What is the ratio of the intensities of the individual waves?
View SolutionTwo sound waves from two different sources interfere at a point to yield a sound of varying intensity. The intensity level between the maximum and minimum is 20 dB. What is the ratio of the intensities of the individual waves?
View Solution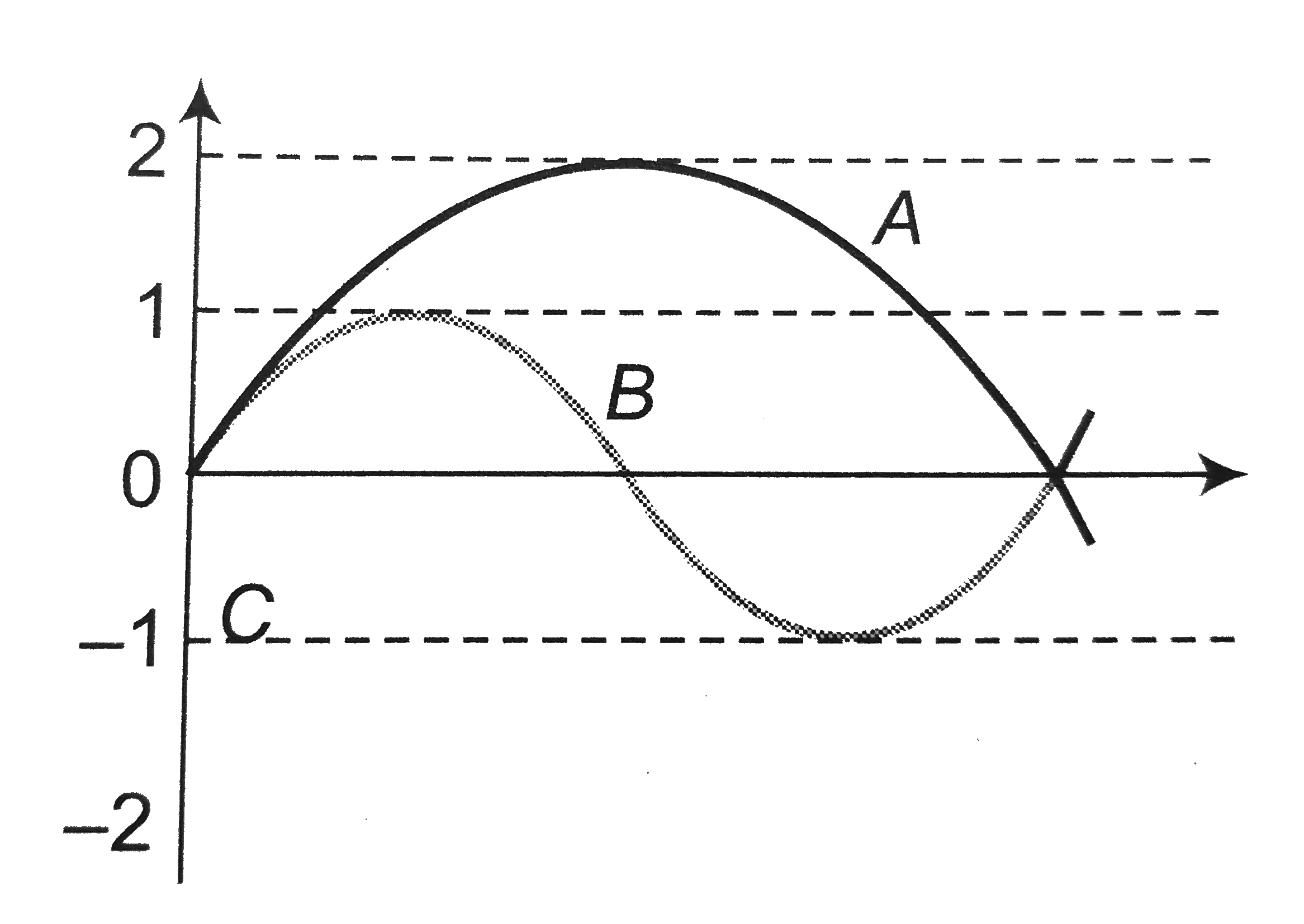
The displacement time graph for two sound waves A and B are shown in the figure. Then the ratio of their intensities IA/IB is equal toView Solution
The displacement time graph for two sound waves A and B are shown in the figure. Then the ratio of their intensities IA/IB is equal toView SolutionThe ratio of the intensities of two interfering waves is 81:1. What is the ratio of the maximum to minimum intensity?
View SolutionIf one sound wave has twice the pressure amplitude of the another sound in the same medium, find the ratio of the intensities of the two sounds ?
View SolutionThe ratio of intensities of two waves is 16:9. What is the ratio of amplitudes? If these two waves produce interference, then find the ratio of maximum and minimum intensities.
View SolutionThe two coherent sources of equal intensity produce maximum intensity of 100 units at a point. If the intensity of one of the sources is reduced by 50% by reducing its width then the intensity of light at the same point will be
View SolutionThe two coherent sources of equal intensity produce maximum intensity of 100 units at a point. If the intensity of one of the sources is reduced by 50% by reducing its width then the intensity of light at the same point will be
View SolutionThe ratio of maximum to minimum intensity due to superposition of two waves is 499. Then, the ratio of the intensity of component waves is.
View Solution

