The length of a brass rod is found to be smaller on a hot summer day that on a cold winter day as measured by the same aluminium scale. Do we conclude that brass shrinks on heating.
To solve the question, we need to analyze the situation regarding the measurements of the brass rod using an aluminum scale on hot summer days compared to cold winter days.
1. Understanding Thermal Expansion:
- When materials are heated, they generally expand. This is known as thermal expansion. Different materials expand at different rates, characterized by their coefficients of linear expansion.
2. Identify the Materials:
- In this scenario, we have a brass rod and an aluminum scale. We need to consider the thermal expansion properties of both materials.
3. Thermal Expansion Coefficients:
- The coefficient of linear expansion for aluminum is greater than that of brass. This means that when both materials are heated, aluminum will expand more than brass.
4. Measurement on a Hot Day:
- On a hot summer day, both the brass rod and the aluminum scale are heated. Since aluminum expands more than brass, the aluminum scale will become longer than the brass rod when both are at the same temperature.
5. Apparent Measurement:
- When measuring the length of the brass rod with the aluminum scale on a hot day, the scale (which has expanded more) will indicate a shorter length for the brass rod than it would on a cold winter day when both materials are at lower temperatures.
6. Conclusion:
- The apparent decrease in the length of the brass rod when measured with the aluminum scale on a hot day does not indicate that brass shrinks upon heating. Instead, it is due to the greater expansion of the aluminum scale compared to the brass rod. Therefore, we cannot conclude that brass shrinks on heating.
Final Conclusion:
The observation that the brass rod appears smaller on a hot day compared to a cold day is a result of the different thermal expansion rates of brass and aluminum, not because brass shrinks when heated.
---
- When materials are heated, they generally expand. This is known as thermal expansion. Different materials expand at different rates, characterized by their coefficients of linear expansion.
- In this scenario, we have a brass rod and an aluminum scale. We need to consider the thermal expansion properties of both materials.
- The coefficient of linear expansion for aluminum is greater than that of brass. This means that when both materials are heated, aluminum will expand more than brass.
- On a hot summer day, both the brass rod and the aluminum scale are heated. Since aluminum expands more than brass, the aluminum scale will become longer than the brass rod when both are at the same temperature.
- When measuring the length of the brass rod with the aluminum scale on a hot day, the scale (which has expanded more) will indicate a shorter length for the brass rod than it would on a cold winter day when both materials are at lower temperatures.
- The apparent decrease in the length of the brass rod when measured with the aluminum scale on a hot day does not indicate that brass shrinks upon heating. Instead, it is due to the greater expansion of the aluminum scale compared to the brass rod. Therefore, we cannot conclude that brass shrinks on heating.
The observation that the brass rod appears smaller on a hot day compared to a cold day is a result of the different thermal expansion rates of brass and aluminum, not because brass shrinks when heated.
Topper's Solved these Questions
- HEAT AND TEMPERATUREBOOK - HC VERMA ENGLISHCHAPTER - HEAT AND TEMPERATUREEXERCISE - Objective 2
6 Videos
- HEAT AND TEMPERATUREBOOK - HC VERMA ENGLISHCHAPTER - HEAT AND TEMPERATUREEXERCISE - Exercise
34 Videos
- GRAVITATIONBOOK - HC VERMA ENGLISHCHAPTER - GRAVITATIONEXERCISE - Question for short Answers
18 Videos
- HEAT TRANSFERBOOK - HC VERMA ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - QUESTIONS FOR SHORT ANSWER
11 Videos
Similar Questions
A steel tape 1m long is correctly calibrated for a temperature of 27∘C. The length of a steel rod measured by this tape is found to be 63.0cm on a hot day when the temperature is 45.0∘C. What is the acutual length of the steel rod on that day? what is the length of the same steel rod on a day when the temperature is 27.0∘C ? coefficient of linear expansion of steel =1.20×10−5.∘C−1.
View SolutionAt room temperature (25∘C) the length of a steel rod is measured using a brass centimetre scale. The measured length is 20 cm. If the scale is calibrated to read accurately at temperature 0∘C, find the actual length of steel rod at room temperature.
View Solution
Knowledge Check
At 50∘C , a brass rod has a length 50 cm and a diameter 2 mm . It is joined to a steel rod of the same length and diameter at the same temperature . The change in the length of the composite rod when it is heated to 250∘C is (Coefficient of linear expansion of brass = 2.0×10−5∘C−1 , coefficient of linear expansion of steel = 1.2×10−5∘C−1)
A0.28 cmB0.30 cmC0.32 cmD0.34 cmThis passage is adapted from Geoffrey Giller, “Long a Mystery, How 500-Meter-High Undersea Waves Form Is Revealed.” ©2014 by Scientific American.
nearly impossible to see. Unlike other large waves, these rollers, called internal waves, do not ride the ocean surface. Instead, they move underwater, undetectable without the use of satellite imagery or sophisticated monitoring equipment. Despite their hidden nature, internal waves are fundamental parts of ocean water dynamics, transferring heat to the ocean depths and bringing up cold water from below. And they can reach staggering heights—some as tall as skyscrapers.
Because these waves are involved in ocean mixing and thus the transfer of heat, understanding them is crucial to global climate modeling, says Tom Peacock, a researcher at the Massachusetts Institute of Technology. Most models fail to take internal waves into account. “If we want to have more and more accurate climate models, we have to be able to capture processes such as this,” Peacock says.
Peacock and his colleagues tried to do just that. Their study, published in November in Geophysical Research Letters, focused on internal waves generated in the Luzon Strait, which separates Taiwan and the Philippines. Internal waves in this region, thought to be some of the largest in the world, can reach about 500 meters high. “That’s the same height as the Freedom Tower that’s just been built in New York,” Peacock says.
the South China Sea and beyond, they didn’t know exactly how internal waves formed. To find out, Peacock and a team of researchers from M.I.T. and Woods Hole Oceanographic Institution worked with France’s National Center for Scientific Research using a giant facility there called the Coriolis Platform. The rotating platform, about 15 meters (49.2 feet) in diameter, turns at variable speeds and can simulate Earth’s rotation. It also has walls, which means scientists can fill it with water and create accurate, large-scale simulations of various oceanographic scenarios.
Peacock and his team built a carbon-fiber resin scale model of the Luzon Strait, including the islands and surrounding ocean floor topography. Then they filled the platform with water of varying salinity to replicate the different densities found at the strait, with denser, saltier water below and lighter, less briny water above. Small particles were added to the solution and illuminated with lights from below in order to track how the liquid moved. Finally, they re-created tides using two large plungers to see how the internal waves themselves formed.
The Luzon Strait’s underwater topography, with a distinct double-ridge shape, turns out to be responsible for generating the underwater waves. As the tide rises and falls and water moves through the strait, colder, denser water is pushed up over the ridges into warmer, less dense layers above it.
This action results in bumps of colder water trailed by warmer water that generate an internal wave. As these waves move toward land, they become steeper—much the same way waves at the beach become taller before they hit the shore—until they break on a continental shelf.
The researchers were also able to devise a mathematical model that describes the movement and formation of these waves. Whereas the model is specific to the Luzon Strait, it can still help researchers understand how internal waves are generated in other places around the world.
Eventually, this information will be incorporated into global climate models, making them more accurate. “It’s very clear, within the context of these [global climate] models, that internal waves play a role in driving ocean circulations,” Peacock says.
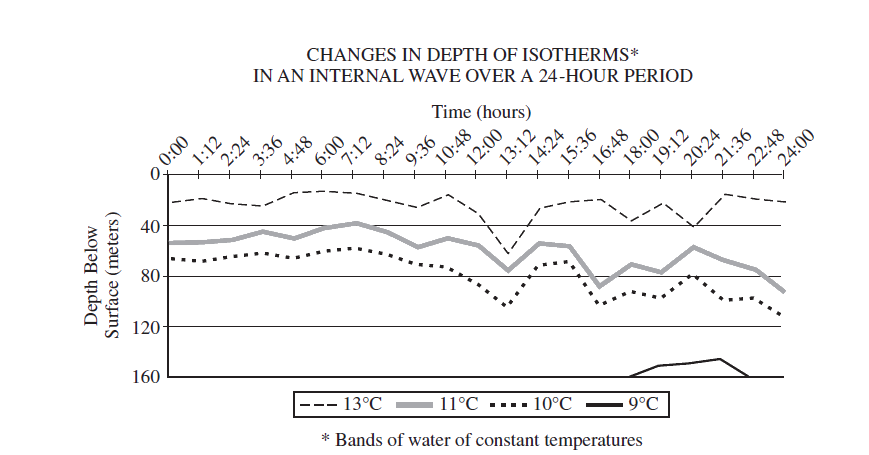
Adapted from Justin Small et al., “Internal Solitons in the Ocean: Prediction from SAR.” ©1998 by Oceanography, Defence Evaluation and Research Agency.
As used in line 65, “devise” most nearly meansAcreate.Bsolve.Cimagine.Dbegin.This passage is adapted from Geoffrey Giller, “Long a Mystery, How 500-Meter-High Undersea Waves Form Is Revealed.” ©2014 by Scientific American.
nearly impossible to see. Unlike other large waves, these rollers, called internal waves, do not ride the ocean surface. Instead, they move underwater, undetectable without the use of satellite imagery or sophisticated monitoring equipment. Despite their hidden nature, internal waves are fundamental parts of ocean water dynamics, transferring heat to the ocean depths and bringing up cold water from below. And they can reach staggering heights—some as tall as skyscrapers.
Because these waves are involved in ocean mixing and thus the transfer of heat, understanding them is crucial to global climate modeling, says Tom Peacock, a researcher at the Massachusetts Institute of Technology. Most models fail to take internal waves into account. “If we want to have more and more accurate climate models, we have to be able to capture processes such as this,” Peacock says.
Peacock and his colleagues tried to do just that. Their study, published in November in Geophysical Research Letters, focused on internal waves generated in the Luzon Strait, which separates Taiwan and the Philippines. Internal waves in this region, thought to be some of the largest in the world, can reach about 500 meters high. “That’s the same height as the Freedom Tower that’s just been built in New York,” Peacock says.
the South China Sea and beyond, they didn’t know exactly how internal waves formed. To find out, Peacock and a team of researchers from M.I.T. and Woods Hole Oceanographic Institution worked with France’s National Center for Scientific Research using a giant facility there called the Coriolis Platform. The rotating platform, about 15 meters (49.2 feet) in diameter, turns at variable speeds and can simulate Earth’s rotation. It also has walls, which means scientists can fill it with water and create accurate, large-scale simulations of various oceanographic scenarios.
Peacock and his team built a carbon-fiber resin scale model of the Luzon Strait, including the islands and surrounding ocean floor topography. Then they filled the platform with water of varying salinity to replicate the different densities found at the strait, with denser, saltier water below and lighter, less briny water above. Small particles were added to the solution and illuminated with lights from below in order to track how the liquid moved. Finally, they re-created tides using two large plungers to see how the internal waves themselves formed.
The Luzon Strait’s underwater topography, with a distinct double-ridge shape, turns out to be responsible for generating the underwater waves. As the tide rises and falls and water moves through the strait, colder, denser water is pushed up over the ridges into warmer, less dense layers above it.
This action results in bumps of colder water trailed by warmer water that generate an internal wave. As these waves move toward land, they become steeper—much the same way waves at the beach become taller before they hit the shore—until they break on a continental shelf.
The researchers were also able to devise a mathematical model that describes the movement and formation of these waves. Whereas the model is specific to the Luzon Strait, it can still help researchers understand how internal waves are generated in other places around the world.
Eventually, this information will be incorporated into global climate models, making them more accurate. “It’s very clear, within the context of these [global climate] models, that internal waves play a role in driving ocean circulations,” Peacock says.
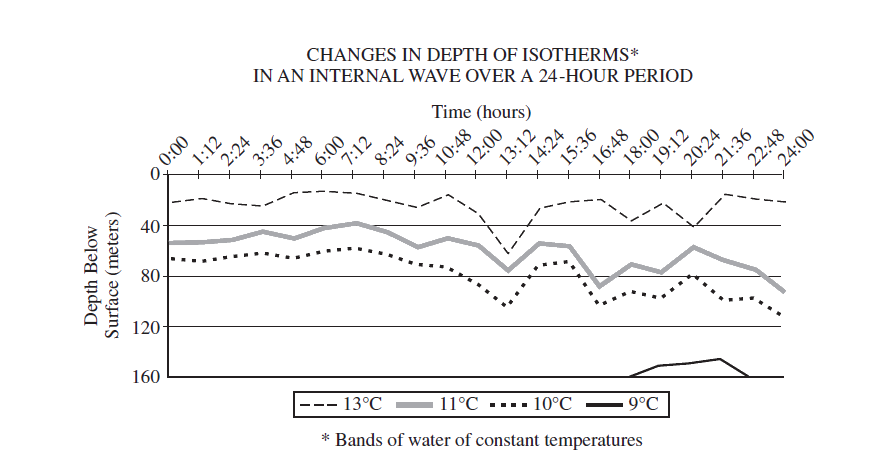
Adapted from Justin Small et al., “Internal Solitons in the Ocean: Prediction from SAR.” ©1998 by Oceanography, Defence Evaluation and Research Agency.
The first paragraph serves mainly toAexplain how a scientific device is used.Bnote a common misconception about an event.Cdescribe a natural phenomenon and address its importance.Dpresent a recent study and summarize its findings.
A meter scale is made up of steel and measures correct length at 16∘C. What will be the percentage error if this scale is used (a) on a summer day when the temperature is 46∘C and (b) on a winter day when the temperature is 6∘C? Coefficient of linear expansion of steel =11×10−6C−1.
View SolutionTwo unifrom brass rod A and B of length l and 2l and radii 2r respectively are heated to the same temperature. The ratio of the increase in the volume of A to that of B is
View SolutionIn a vernier callipers the main scale and the vernier scale are made up different materials. When the room temperature increases by ΔT∘C, it is found the reading of the instrument remains the same. Earlier it was observed that the front edge of the wooden rod placed for measurement crossed the Nth main scale division and N + 2 MSD coincided with the 2nd VSD. Initially, 10 VSD coincided with 9MSD. If coefficient of linear expansion of the main scale is α1 and that of the vernier scale is α2 then what is the value of α1/α2 ? (Ignore the expansion of the rod on heating)
View SolutionOn a cold winter day, the atmospheric temperature is −θ (on celsius scale) which is below 0∘C. A cylindrical drum of height h made of a bad conductor is completely filled with water at 0∘C and is kept outside without any lid. Calculate the time taken for the whole mass of water to freeze. Thermal conductivity of ice is K and its latent heat of fusion is L. Neglect expansion of water on freezing.

View SolutionThis passage is adapted from Geoffrey Giller, “Long a Mystery, How 500-Meter-High Undersea Waves Form Is Revealed.” ©2014 by Scientific American.
nearly impossible to see. Unlike other large waves, these rollers, called internal waves, do not ride the ocean surface. Instead, they move underwater, undetectable without the use of satellite imagery or sophisticated monitoring equipment. Despite their hidden nature, internal waves are fundamental parts of ocean water dynamics, transferring heat to the ocean depths and bringing up cold water from below. And they can reach staggering heights—some as tall as skyscrapers.
Because these waves are involved in ocean mixing and thus the transfer of heat, understanding them is crucial to global climate modeling, says Tom Peacock, a researcher at the Massachusetts Institute of Technology. Most models fail to take internal waves into account. “If we want to have more and more accurate climate models, we have to be able to capture processes such as this,” Peacock says.
Peacock and his colleagues tried to do just that. Their study, published in November in Geophysical Research Letters, focused on internal waves generated in the Luzon Strait, which separates Taiwan and the Philippines. Internal waves in this region, thought to be some of the largest in the world, can reach about 500 meters high. “That’s the same height as the Freedom Tower that’s just been built in New York,” Peacock says.
the South China Sea and beyond, they didn’t know exactly how internal waves formed. To find out, Peacock and a team of researchers from M.I.T. and Woods Hole Oceanographic Institution worked with France’s National Center for Scientific Research using a giant facility there called the Coriolis Platform. The rotating platform, about 15 meters (49.2 feet) in diameter, turns at variable speeds and can simulate Earth’s rotation. It also has walls, which means scientists can fill it with water and create accurate, large-scale simulations of various oceanographic scenarios.
Peacock and his team built a carbon-fiber resin scale model of the Luzon Strait, including the islands and surrounding ocean floor topography. Then they filled the platform with water of varying salinity to replicate the different densities found at the strait, with denser, saltier water below and lighter, less briny water above. Small particles were added to the solution and illuminated with lights from below in order to track how the liquid moved. Finally, they re-created tides using two large plungers to see how the internal waves themselves formed.
The Luzon Strait’s underwater topography, with a distinct double-ridge shape, turns out to be responsible for generating the underwater waves. As the tide rises and falls and water moves through the strait, colder, denser water is pushed up over the ridges into warmer, less dense layers above it.
This action results in bumps of colder water trailed by warmer water that generate an internal wave. As these waves move toward land, they become steeper—much the same way waves at the beach become taller before they hit the shore—until they break on a continental shelf.
The researchers were also able to devise a mathematical model that describes the movement and formation of these waves. Whereas the model is specific to the Luzon Strait, it can still help researchers understand how internal waves are generated in other places around the world.
Eventually, this information will be incorporated into global climate models, making them more accurate. “It’s very clear, within the context of these [global climate] models, that internal waves play a role in driving ocean circulations,” Peacock says.
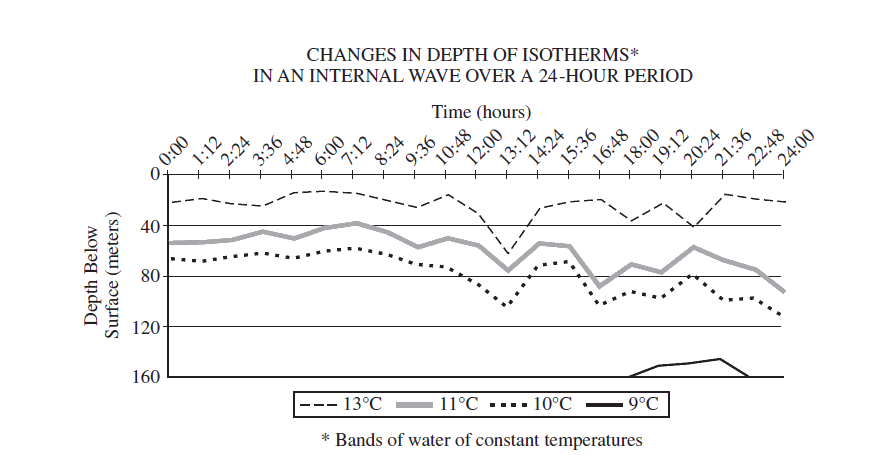
Adapted from Justin Small et al., “Internal Solitons in the Ocean: Prediction from SAR.” ©1998 by Oceanography, Defence Evaluation and Research Agency.
According to Peacock, the ability to monitor internal waves is significant primarily because
View Solution
