The length of the two rods made up of the same metal and having the same area of cross-section are 0.6 m and 0.8 m respectively. The temperature between the ends of first rod is 90∘ C and 60∘ C and that for the other rod is 150 and 110∘ C. For which rod the rate of conduction will be greater
First
Second
Same for both
None of the above
The correct Answer is:C
To determine which rod has a greater rate of conduction, we will use the formula for heat conduction, which is given by Fourier's law:
QT=K⋅A⋅(ΔT)L
Where:
- Q is the heat transferred,
- T is the time,
- K is the thermal conductivity of the material,
- A is the cross-sectional area,
- ΔT is the temperature difference between the ends of the rod,
- L is the length of the rod.
Step 1: Identify the parameters for both rods
- Rod 1:
- Length L1=0.6m
- Temperature difference ΔT1=90∘C−60∘C=30∘C
- Rod 2:
- Length L2=0.8m
- Temperature difference ΔT2=150∘C−110∘C=40∘C
Step 2: Calculate the rate of heat transfer for Rod 1
Using the formula for Rod 1:
Q1T=K⋅A⋅ΔT1L1
Substituting the values:
Q1T=K⋅A⋅300.6
This simplifies to:
Q1T=K⋅A⋅50
Step 3: Calculate the rate of heat transfer for Rod 2
Using the formula for Rod 2:
Q2T=K⋅A⋅ΔT2L2
Substituting the values:
Q2T=K⋅A⋅400.8
This simplifies to:
Q2T=K⋅A⋅50
Step 4: Compare the rates of heat transfer
From the calculations, we find:
- For Rod 1, Q1T=K⋅A⋅50
- For Rod 2, Q2T=K⋅A⋅50
Both rods have the same rate of heat transfer.
Conclusion
The rate of conduction is the same for both rods.
Final Answer: Both rods have the same rate of conduction.
---
- Q is the heat transferred,
- T is the time,
- K is the thermal conductivity of the material,
- A is the cross-sectional area,
- ΔT is the temperature difference between the ends of the rod,
- L is the length of the rod.
- Rod 1:
- Length L1=0.6m
- Temperature difference ΔT1=90∘C−60∘C=30∘C
- Length L2=0.8m
- Temperature difference ΔT2=150∘C−110∘C=40∘C
Using the formula for Rod 1:
Using the formula for Rod 2:
From the calculations, we find:
- For Rod 2, Q2T=K⋅A⋅50
The rate of conduction is the same for both rods.
Topper's Solved these Questions
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Check points 16.4
29 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Taking it together
51 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Check point 16.2
10 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 Subjective
14 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
Similar Questions
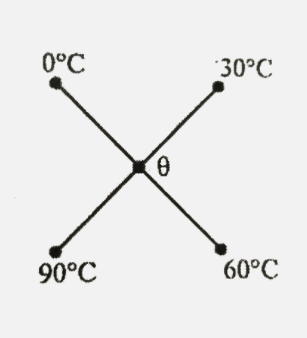
Four rods of same material and having the same cross section and length have been joined, as shown. The temperature of the junction of four rods will be :
View SolutionTwo rods P and Q of equal lengths have thermal conductivities K1andK2 and cross-sectional areas A1andA2 respectively. If the temperature difference across the ends of each rod is the same, then the condition for which the rate of flow of heat through each of them will be equal, is
View SolutionThree rods are made from the same material and having the same cross-sectional area and length have been joined as shown in the figure.
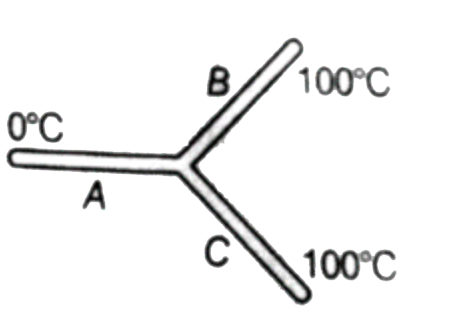
The left end and right end are kept 0∘Cand100∘C , respectively . The temperature of the junction of three rods will be
View SolutionThe temperature gradient in a rod of 0.5m length is 80∘C/m. It the temperature of hotter end of the rod is 30∘C, then the temperature of the cooler end is
View SolutionTwo ends of a conducting rod of varying cross-section are maintained at 200∘C and 0∘C respectively. In steady state:

View SolutionOne end of conducting rod is maintained at temperature 50∘C and at the other end ice is melting at 0∘C. The rate of melting of ice is doubled if:
View SolutionThe end of two rods of different materials with their thermal conductivities, area of cross-section and lengths all in the ratio 1:2 are maintained at the same temperature difference. If the rate of flow of heat in the first rod is 4cal/s. Then, in the second rod rate of heat flow in cal/s will be
View SolutionFigure shows a copper rod joined to a steel rod. The rods have equal length and and the equal cross sectional area. The free end of the copper rod is kept at 0∘C and that of the steel rod is kept at 100∘C . Find the temperature at the junction of the rods. conductivity of copper =390Wm−1C−1 and that of steel =46Wm−1C−1 .

View SolutionThree rods of the same length and the same area of the cross-section are joined. The temperature of two ends one T1 and T2 as shown in the figure.
 As we move along the rod the variation of temperature are as shown in the following [Rods are insulated from the surrounding except at the faces]
As we move along the rod the variation of temperature are as shown in the following [Rods are insulated from the surrounding except at the faces]

View SolutionThree rods made of the same material and having the same cross-section have been joined as shown in the figure. Each rod is of the same length. The left and right ends are kept at 0∘C and 90∘C, respectively. The temperature of junction of the three rods will be
(a) 45∘C (b) 60∘C
(c) 30∘C (d) 20∘C.

View Solution
