The unit of thermal conductivity is :
Js−1K
Js−1m2k
Jm−1K
Js−1m−1K−1
The correct Answer is:D
To find the unit of thermal conductivity, we start with the formula that relates heat transfer to thermal conductivity. The formula is:
q=k⋅A⋅ΔTL
Where:
- q is the heat transferred (in joules, J)
- k is the thermal conductivity (what we want to find)
- A is the area through which heat is being transferred (in square meters, m²)
- ΔT is the temperature difference (in Kelvin, K)
- L is the length of the material (in meters, m)
We can rearrange this formula to solve for k:
k=q⋅LA⋅ΔT
Now, we need to determine the units of each component in this equation:
1. The unit of heat q is joules (J).
2. The unit of length L is meters (m).
3. The unit of area A is square meters (m²).
4. The unit of temperature difference ΔT is Kelvin (K).
Substituting these units into the equation for k:
k=J⋅mm2⋅K
Now, simplifying this expression:
- The meter in the numerator and one of the meters in the denominator will cancel out:
k=Jm⋅K
Next, we need to consider the time factor. The heat transfer occurs over a period of time, which is typically measured in seconds (s). Therefore, we can express the thermal conductivity in terms of time:
k=Jm⋅K⋅s
Thus, the unit of thermal conductivity can be expressed as:
k=Js⋅m⋅K
In conclusion, the unit of thermal conductivity is:
Joule per second per meter per Kelvin (J/s·m·K).
- q is the heat transferred (in joules, J)
- k is the thermal conductivity (what we want to find)
- A is the area through which heat is being transferred (in square meters, m²)
- ΔT is the temperature difference (in Kelvin, K)
- L is the length of the material (in meters, m)
2. The unit of length L is meters (m).
3. The unit of area A is square meters (m²).
4. The unit of temperature difference ΔT is Kelvin (K).
Topper's Solved these Questions
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Check points 16.4
29 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Taking it together
51 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Check point 16.2
10 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 Subjective
14 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
Similar Questions
Knowledge Check
Two rods of length l1andl2 and coefficients of thermal conductivities k1andK2 are kept touching each other. Both have the same area of cross-section. The equivalent of thermal conductivity is
AK1+K2BK1l1+K2l2CK1l1+K2l2l1+l2Dl1+l2(l1/K1)+(l2/K2)
The dimensions of coefficient of thermal conductivity is
View SolutionCoefficient of thermal conductivity has the dimensions:
View SolutionThree rods of same dimension are joined in series having thermal conductivity k1 , k2 and k3. The equivalent thermal conductivity is
View Solution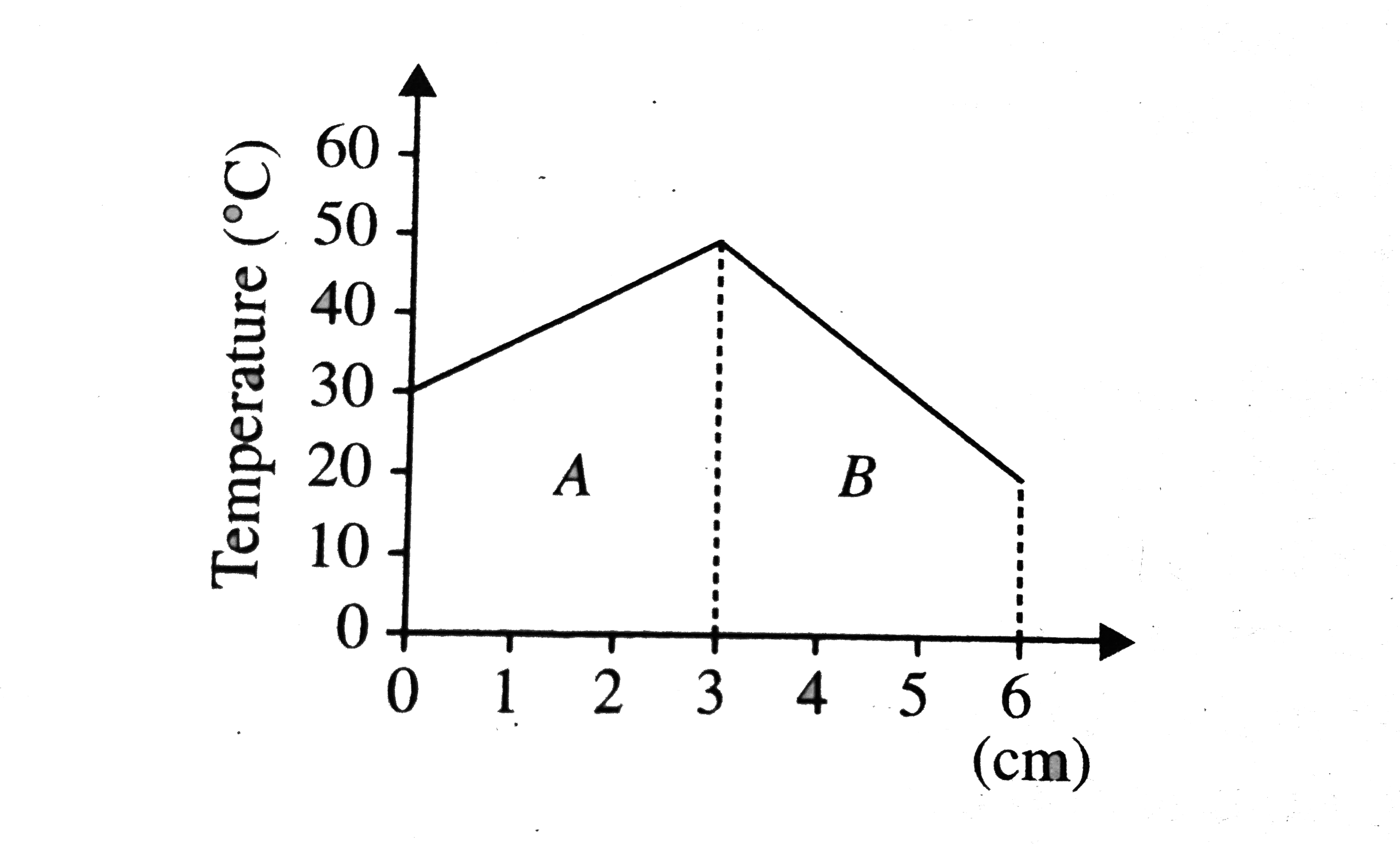
The temperature across two different slabs A and B are shown I the steady state (as shown Fig) The ratio of thermal conductivities of A and B is
View Solution
The temperature across two different slabs A and B are shown I the steady state (as shown Fig) The ratio of thermal conductivities of A and B is
View SolutionThe ratio of thermal conductivity of two rods of different material is 5:4. The two rods of same area of cross-section and same thermal resistance will have the lengths in the ratio
View SolutionCoefficient of thermal conductivity is the product of heat, distance and reciprocal of (area x difference in temperature x time). The new value of a unit of coefficient of thermal conductivity, if fundamental units are 21.6 kg, 1 decimetre, 4 K and 1 minute will be ______ ×10−6 new units.
View Solution
