The linear charge density on a dielectric ring of radius R vanes with θ as λ=λ0cosθ/2, where λ0 is constant. Find the potential at the center O of the ring [in volt].
The correct Answer is:0
To find the potential at the center O of a dielectric ring with a varying linear charge density, we can follow these steps:
Step 1: Define the linear charge density
The linear charge density on the ring is given by:
λ(θ)=λ0cos(θ2)
where λ0 is a constant.
Step 2: Express the differential charge element
The differential charge element dq on a small segment of the ring can be expressed as:
dq=λ(θ)dℓ
where dℓ=Rdθ is the arc length corresponding to the angle dθ. Thus,
dq=λ0cos(θ2)Rdθ
Step 3: Calculate the differential potential dV
The potential dV at the center O due to the charge dq is given by:
dV=kdqR
Substituting for dq:
dV=kλ0cos(θ2)RdθR=kλ0cos(θ2)dθ
Step 4: Integrate to find the total potential V
To find the total potential V at the center O, we integrate dV from θ=0 to θ=2π:
V=∫2π0kλ0cos(θ2)dθ
Step 5: Solve the integral
To solve the integral, we can use the substitution u=θ2, which gives dθ=2du. The limits change as follows: when θ=0, u=0 and when θ=2π, u=π:
V=∫π0kλ0cos(u)⋅2du=2kλ0∫π0cos(u)du
The integral of cos(u) from 0 to π is:
∫π0cos(u)du=(sin(u))π0=sin(π)−sin(0)=0−0=0
Thus,
V=2kλ0⋅0=0
Final Result
The potential at the center O of the ring is:
V=0volts
The linear charge density on the ring is given by:
λ(θ)=λ0cos(θ2)
where λ0 is a constant.
The differential charge element dq on a small segment of the ring can be expressed as:
dq=λ(θ)dℓ
where dℓ=Rdθ is the arc length corresponding to the angle dθ. Thus,
dq=λ0cos(θ2)Rdθ
The potential dV at the center O due to the charge dq is given by:
dV=kdqR
Substituting for dq:
dV=kλ0cos(θ2)RdθR=kλ0cos(θ2)dθ
To find the total potential V at the center O, we integrate dV from θ=0 to θ=2π:
V=∫2π0kλ0cos(θ2)dθ
To solve the integral, we can use the substitution u=θ2, which gives dθ=2du. The limits change as follows: when θ=0, u=0 and when θ=2π, u=π:
V=∫π0kλ0cos(u)⋅2du=2kλ0∫π0cos(u)du
The integral of cos(u) from 0 to π is:
∫π0cos(u)du=(sin(u))π0=sin(π)−sin(0)=0−0=0
Thus,
V=2kλ0⋅0=0
The potential at the center O of the ring is:
V=0volts
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.1
14 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.2
15 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Comprehension
31 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
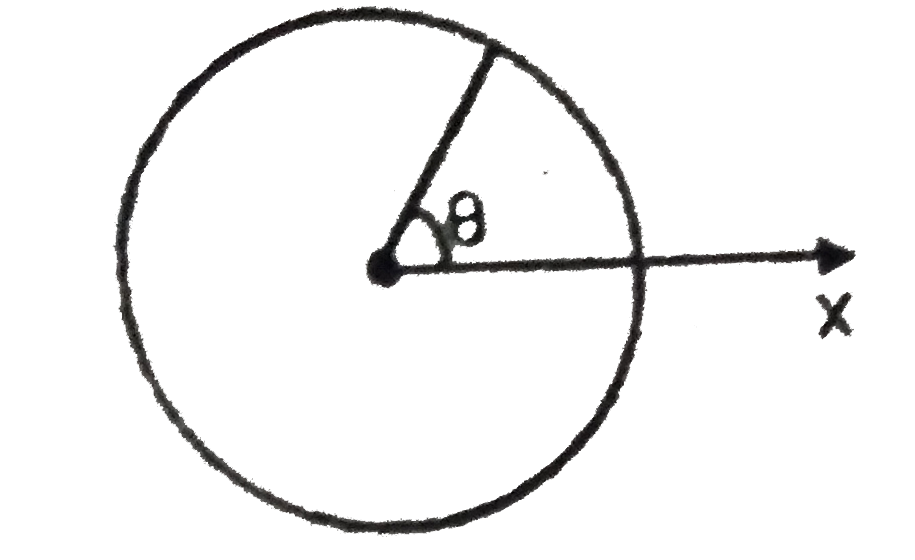
The linear charge density on a ring of radius R is λ=λ0sin(θ) where λ0 is a constant and θ is angle of radius vector of any point on the ring with x-axis. The electric potential at centre of ring is
View SolutionA thin nonconducting ring of radius R has a linear charge density λ=λ0cosφ, where λ0 is a constant , ϕ is the azimuthal angle. Find the magnitude of the electric field strength
(a) at the centre of the ring ,
(b) on the axis of the ring as a function of the distance x from its centre. Investegation the obtained function at x>>R.
View Solutionthe linear charge density of a thin metallic rod varies with the distance x from the end as λ=λ0x2(0≤x≤l) The total charge on the rod is
View SolutionA ring of radius R carries a non - uniform charge of linear density λ=λ0cosθ sec in the figure) Magnitude of the net dipolement of the ring is :

View SolutionA half ring of radius r has a linear charge density λ.The potential at the centre of the half ring is
View SolutionLinear mass density of a rod AB(of≤n>h10m) varies with distance x from its end A as λ =λ0x3 (λ0 is positive constant) . Distance of centre of mass of the rod , from end B is
View SolutionLinear mass density of a rod AB ( of length 10 m) varied with distance x from its end A as λ=λ0x3 (λ0 is poitive constant). Distance of centre of mass the rod, form end B is
View SolutionThe given two fixed rings of radius R lie in XY plane as shown in the figure. Linear charge density of the rings A and B varies as per the relationλ=λ0sinθ and λ=λ0cosθ respectively where theta is measured from +x axis. Distance between the centre of the two rings is r>>R
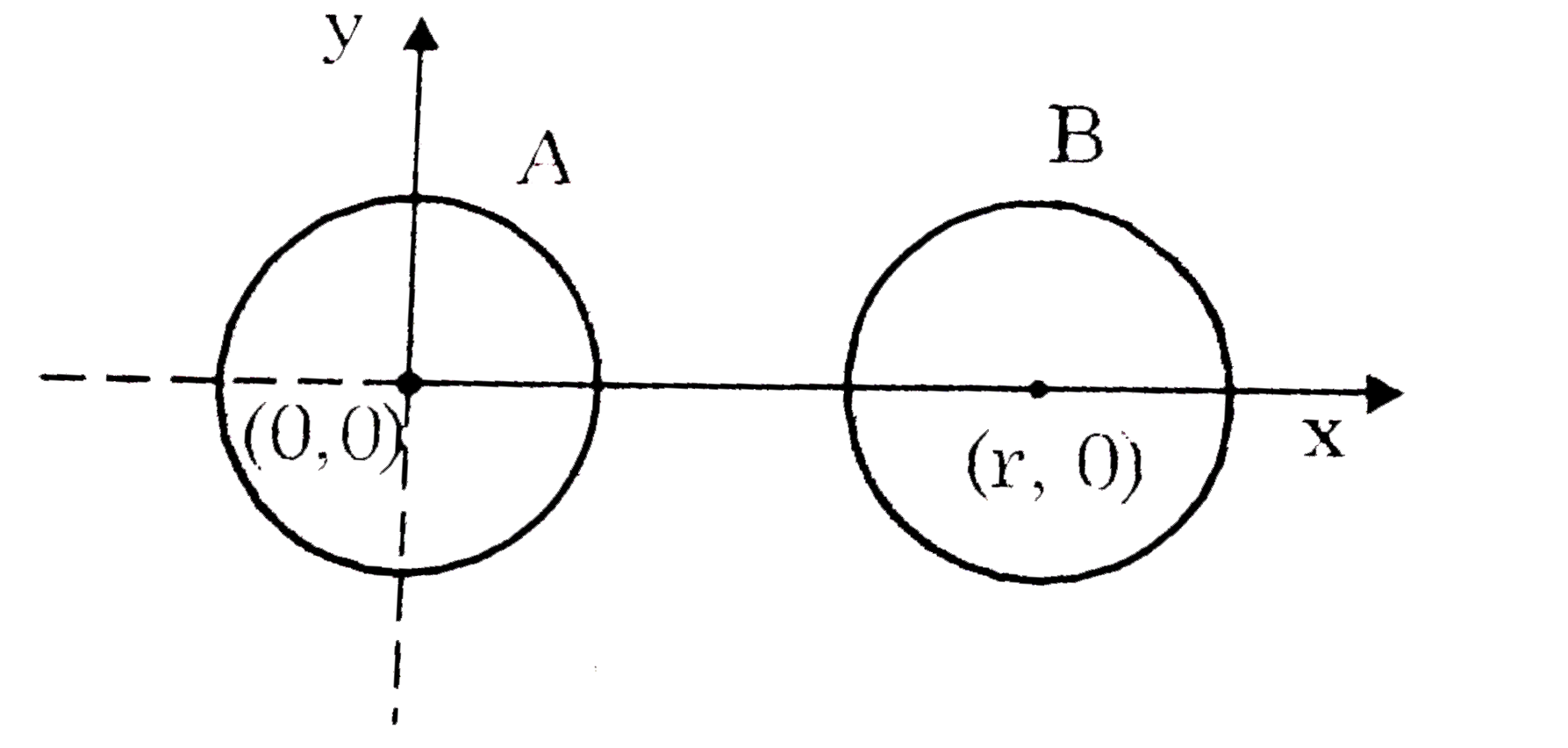
View SolutionThe linear charge density on upper half of semi-circular section of ring is λ and that at lower half is −λ. The direction of electric field at centre O of ring is :

View SolutionThe set of values of λ∈R such that tan2θ+secθ=λ holds for some θ is
View Solution
