The loaded bucket of a craneachievers a maximum velocity 5m/s in some time at a uniform rate and thentakes half of this time to stop at a uniform rate after the application of brake. The time differnce between the instants when half of the maximum velocity is achieved is t(sec). Find the displacement of the bucket.
The correct Answer is:5m
Velocity time curve of the process is shown. Acceleration before applecation of brake,
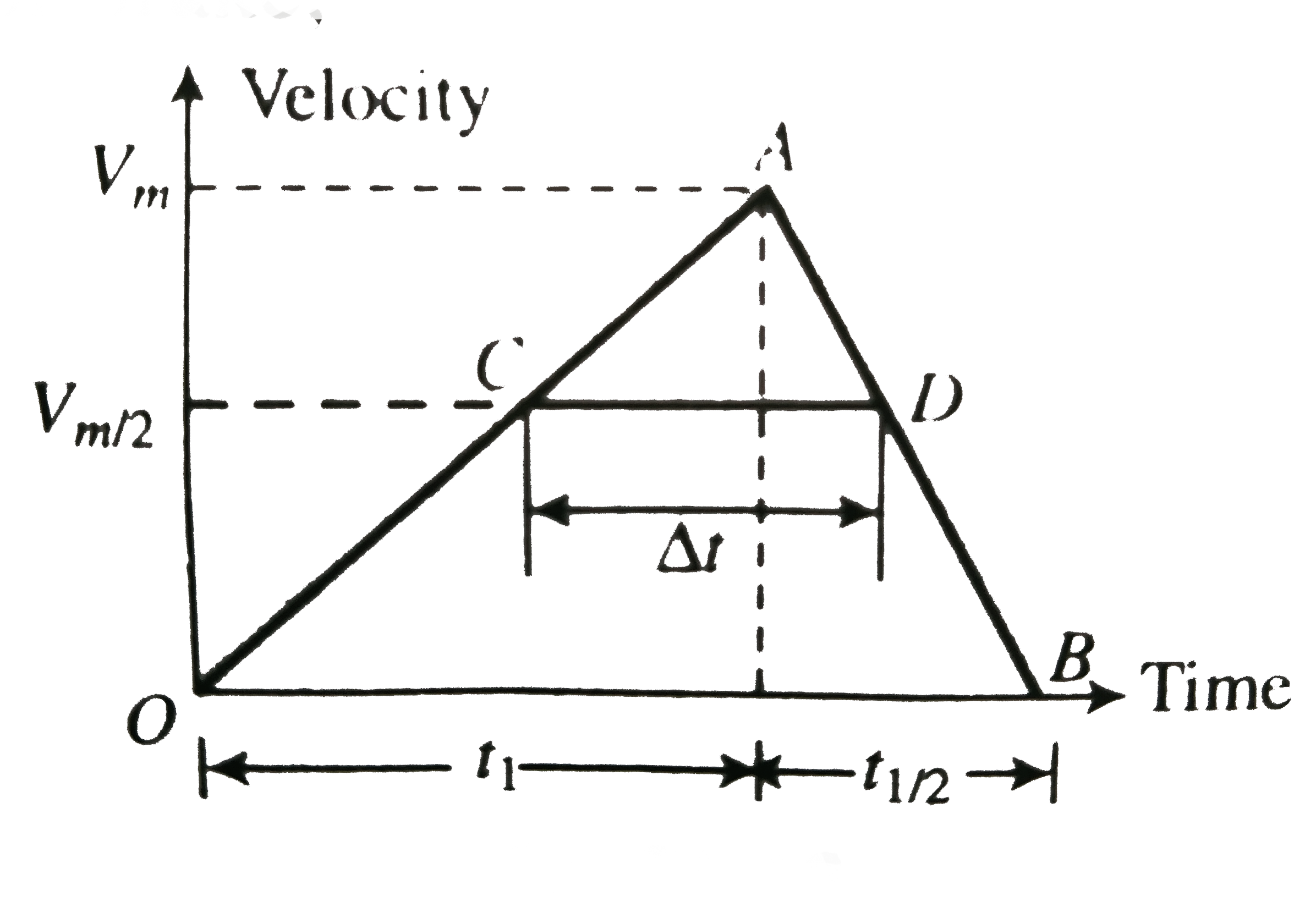 .
.
a1=vmt1⇒t1=vma1 (i)
Displacement =(1/2)vm
(t1+t2/2)
But velocity (vm/2) is observed at C and D.
CD=Δ=Δt=1s (given)
C and D are mid-points of OA and OB .
From similar triangles, OB=(t1_t2/2)=2CD=2Δt
Displacement=(12)vm(2Δt)=vmΔt=5×1=5m,
Topper's Solved these Questions
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Single Correct
52 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Graphical Concept
17 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.4
16 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
Similar Questions
A car accelerates from rest at a constant rate α for some time, after which it decelerates at a constant rate β, to come to rest. If the total time elapsed is t seconds. Then evalute the maximum velocity aquired by the car is
View SolutionGiven that x=120−15t−6t2+t3(t>0), find the time when the velocity is zero. Find the displacement at this instant.
View Solution
Knowledge Check
A car accelerates from rest at a constant rate for some time after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t, the maximum velocity acquired by the car is given by :
Aαβα+βtBα+βαβtCα2+β2βαDα+β2βαA particle starts with S.H.M. from the mean position as shown in the figure. Its amplitude is A and its time period is T. At any instant, its speed is half that of the maximum speed. What is the displacement of the particle at the that point?
 A2A√3B3A√2C√2A3D√3A2
A2A√3B3A√2C√2A3D√3A2
A car of 1000 kg moving with a velocity of30m/s stops with uniform acceleration after covering a distance of 50 m on application of brakes. Find the force applied by the brakes on the car and also work done.
View SolutionA car accelerates from rest at a constant rate 'alpha' for some time after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t, the maximum velocity acquired by the car is given by :
View SolutionA bus accelerates from rest at a constant rate α for some time, after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t seconds then, evaluate.
(a)the maximum velocity achieved and (b)the total distance travelled graphically.
View SolutionA car acceleration form rest at a constant rate α for some time, after which it decelerates at a constant rate β, to come to rest. If the total time elapsed is t evaluate (a) the maximum velocity attained and (b) the total distance travelled.
View SolutionA particle accelerates from rest at a constant rate for some time and attains a velocity of 8 m/sec. Afterwards it decelerates with the constant rate and comes to rest. If the total time taken is 4 sec, the distance travelled is
View Solution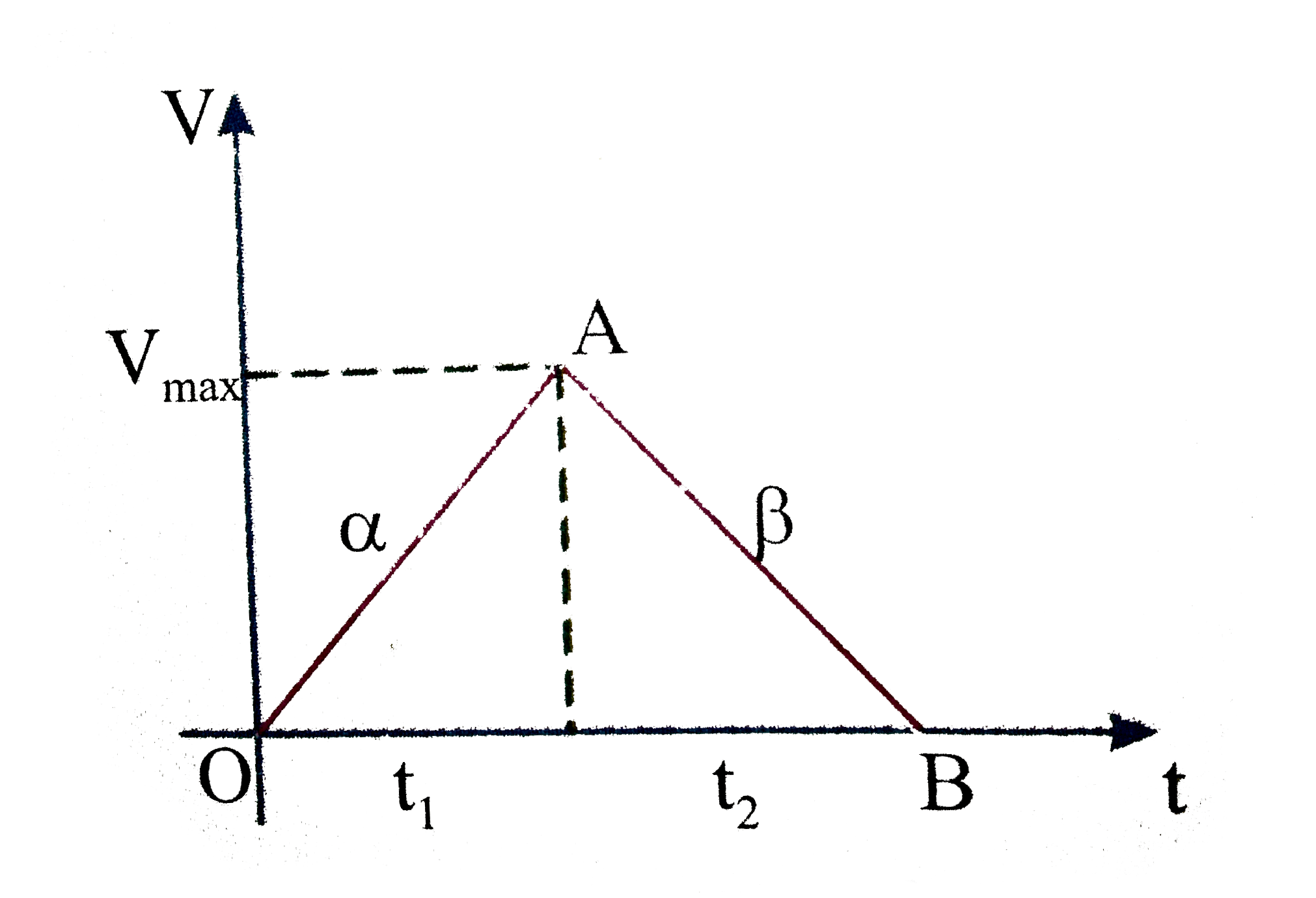
A bus accelerated from rest at a constant rate α for some time, after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t seconds. Then evaluate following parameters from the given graph
(a) the maximum velocity achieved.
(b) the total distance travelled graphically and
(c) Average velocity.
View Solution
