The location of a particale is changed. What can we say about the displacement and distance coverd by the particle?
Both cannot be zero
One of the two may be zero
Both must be zero
Both must be equal
The correct Answer is:A
To analyze the change in location of a particle and understand the concepts of displacement and distance, we can break down the solution into the following steps:
1. Understanding the Definitions:
- Distance: It is the total length of the path traveled by the particle, irrespective of the direction.
- Displacement: It is the shortest straight line distance from the initial position to the final position of the particle, along with the direction.
2. Consider the Initial and Final Positions:
- Let’s denote the initial position of the particle as point A and the final position as point B.
3. Path Traveled:
- When the particle moves from point A to point B, it covers a certain distance. This distance can be represented as the length of the path taken by the particle.
4. Calculating Distance:
- The distance covered by the particle is always a positive value and is equal to the actual path length traveled from A to B.
5. Calculating Displacement:
- The displacement is calculated as the straight line distance from point A to point B. This value can be zero only if the particle returns to its original position (i.e., A = B).
6. Conclusion:
- If the location of the particle changes (i.e., it moves from A to B), then:
- The distance covered is greater than zero.
- The displacement is also greater than zero unless the particle returns to its original position.
- Therefore, both distance and displacement cannot be zero if the particle has changed its location.
Final Statement:
In conclusion, when the location of a particle is changed, both the distance covered and the displacement cannot be zero.
---
- Distance: It is the total length of the path traveled by the particle, irrespective of the direction.
- Displacement: It is the shortest straight line distance from the initial position to the final position of the particle, along with the direction.
- Let’s denote the initial position of the particle as point A and the final position as point B.
- When the particle moves from point A to point B, it covers a certain distance. This distance can be represented as the length of the path taken by the particle.
- The distance covered by the particle is always a positive value and is equal to the actual path length traveled from A to B.
- The displacement is calculated as the straight line distance from point A to point B. This value can be zero only if the particle returns to its original position (i.e., A = B).
- If the location of the particle changes (i.e., it moves from A to B), then:
- The distance covered is greater than zero.
- The displacement is also greater than zero unless the particle returns to its original position.
- Therefore, both distance and displacement cannot be zero if the particle has changed its location.
In conclusion, when the location of a particle is changed, both the distance covered and the displacement cannot be zero.
Topper's Solved these Questions
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Graphical Concept
Explore 17 Videos
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Graphical cancept
Explore 1 Video
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Subjective
Explore 29 Videos
- GRAVITATIONBook:CENGAGE PHYSICS ENGLISHChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise Integer
Explore 9 Videos
Similar Questions
The location of a particle is changed. What can we say about the displacement and distance covered by the particle?
View SolutionA particle is projected vertically upwards from ground with initial velocity u.
a. Find the maximum height H the particle will attain and time T that it will attain and time T that it will take to return to the ground .
 .
.
b. What is the velocity when the particle returns to the ground?
c. What is the displacement and distance travelled by the particle during this time of whole motion.
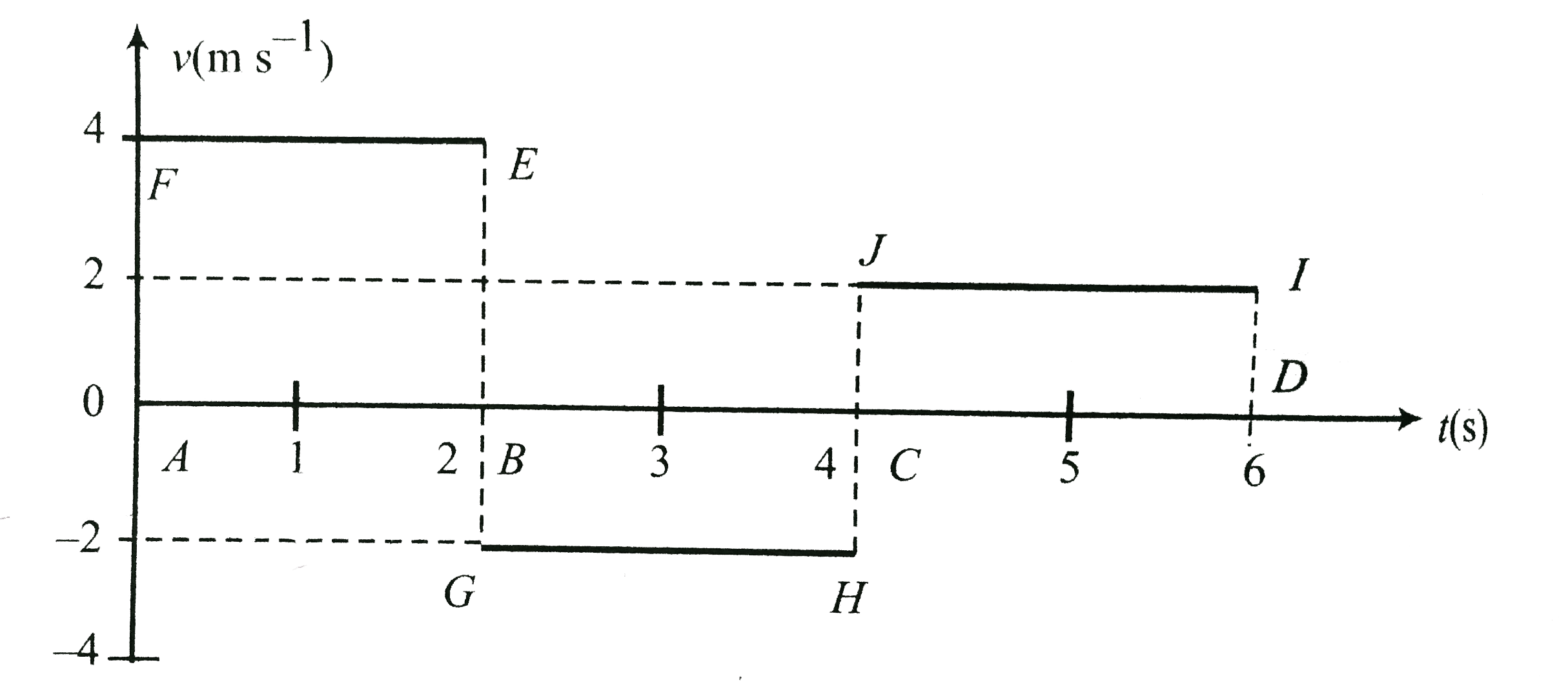
View SolutionThe velocity-time graph of a particle moving in a staight line is shown in the . Find the displacement and the distance trav elled by the particle in 6s.
 .
.
View SolutionIf distance coverd by a particle is zero , what can be its displacement ?
View SolutionCan we add displacement and force vectors ?
View SolutionIf the average velocity of an object is zero in some time interval , what can you say about the displacement of the object for that interval?
View SolutionThe displacement of a particle is moving by x=(t−2)2 where x is in metres and t in second. The distance covered by the particle in first 4 seconds is.
View SolutionIf the displacement of a particle is zero, then distance covered by it
View SolutionIf the displacement of a particle is zero, then distance covered by it
View SolutionA particle has an initial velocity of 9m/s due east and a constant acceleration of 2m/s2 due west. The distance coverd by the particle in the fifth second of its motion is :
View Solution