The magnetic flux through a coil perpendicular to its plane and directed into paper is varying according to the relation ϕ=(5t2+10t+5) milliweber. Calculate the e.m.f. induced in the loop at t=5 s.
To solve the problem, we need to calculate the induced electromotive force (e.m.f.) in the coil at t=5 seconds, given the magnetic flux through the coil as a function of time. The magnetic flux is given by the equation:
ϕ(t)=5t2+10t+5milliweber
1. Understand the formula for induced e.m.f.:
The induced e.m.f. (E) in a coil is given by Faraday's law of electromagnetic induction, which states:
E=−dϕdt
Here, ϕ is the magnetic flux.
2. Differentiate the magnetic flux:
We need to find the derivative of the magnetic flux ϕ(t) with respect to time t:
ϕ(t)=5t2+10t+5
Taking the derivative:
dϕdt=ddt(5t2+10t+5)
Using the power rule of differentiation:
dϕdt=10t+10
3. Substitute t=5 seconds into the derivative:
Now, we will substitute t=5 seconds into the derivative to find the induced e.m.f.:
dϕdt∣∣∣t=5=10(5)+10=50+10=60
4. Calculate the induced e.m.f.:
Now, we can find the e.m.f.:
E=−dϕdt=−60milliweber/second
Since we are interested in the magnitude of the induced e.m.f., we take the absolute value:
|E|=60milliweber/second
5. Convert milliweber to volts:
Since 1 milliweber = 10−3 weber, the induced e.m.f. in volts is:
|E|=60×10−3V=0.06V
Final Answer:
The induced e.m.f. in the loop at t=5 seconds is 0.06V.
The induced e.m.f. (E) in a coil is given by Faraday's law of electromagnetic induction, which states:
E=−dϕdt
Here, ϕ is the magnetic flux.
We need to find the derivative of the magnetic flux ϕ(t) with respect to time t:
ϕ(t)=5t2+10t+5
Taking the derivative:
dϕdt=ddt(5t2+10t+5)
Using the power rule of differentiation:
dϕdt=10t+10
Now, we will substitute t=5 seconds into the derivative to find the induced e.m.f.:
dϕdt∣∣∣t=5=10(5)+10=50+10=60
Now, we can find the e.m.f.:
E=−dϕdt=−60milliweber/second
Since we are interested in the magnitude of the induced e.m.f., we take the absolute value:
|E|=60milliweber/second
Since 1 milliweber = 10−3 weber, the induced e.m.f. in volts is:
|E|=60×10−3V=0.06V
The induced e.m.f. in the loop at t=5 seconds is 0.06V.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Solved Examples (b)1videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Short Answer Qusetions2videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
- BOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise191videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - II Focus multiple choice question5videos
ELECTROMAGNETIC WAVES
Similar Questions
The magnetic flux passing perpendicular to the plane of the coil and directed into the paper is varying according to the relation ϕ=3t2+2t+3, where ϕ is in milliweber and t is in second. Then the magnitude of emf induced in the loop when t=2 second is-
 View Solution
View SolutionThe magnetic flux through a loop is varying according to relation ϕ=6t2+7t+1 where ϕ is in milliweber and t is in second. What is the e.m.f. induced in the loop at t = 2 second ?
View Solution
Knowledge Check
- Question 1 - Select One
The magnetic flux through a coil perpendicular to its plane and directed into paper is varying according to the relation ϕ=(2t2+4t+6)mWb. The emf induced in the loop at t=4 s is
A0.12 VB2.4 VC0.02 VD1.2 V - Question 2 - Select One
In the figure the flux through the loop perpendicular to the plane of the coil and direciton into the paper varying according to the relation ϕ=6t2+7t+I where ϕ is in milliweber and t is in loop at t=2s and direction of induced current through R are
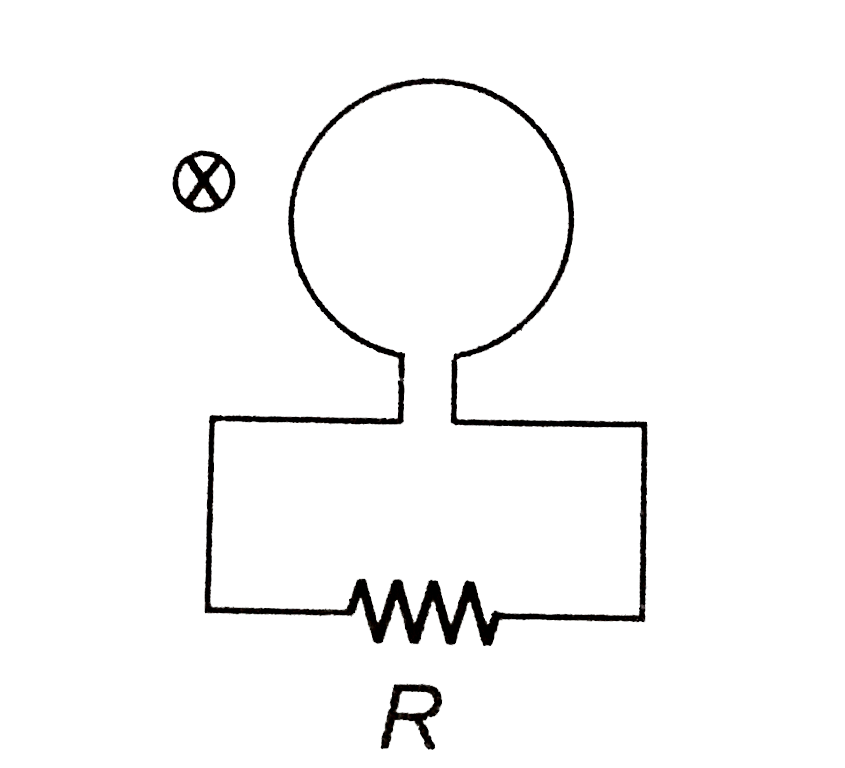 A39mV , right to leftB39mV , left to rightC31mV right to leftD31mV , left to right
A39mV , right to leftB39mV , left to rightC31mV right to leftD31mV , left to right - Question 3 - Select One
The magnetic flux linked with a coil is ϕ=(3t2−2t+1) milliweber. The e.m.f. induced in the coil at t = 1 sec is
A4 VB4×10−3VC6 VD4×103V
The magnetic flux passing prependicular to the plane of the coil directed into the paper is varying according to the relation
ϕ=6t2+8t+I0 , where ϕ is in weber and t in second.
(a) What is the magnitude of emf induced in the loop when t=2sec ?
(b) What is the magnitude and direction of current at t=2sec ?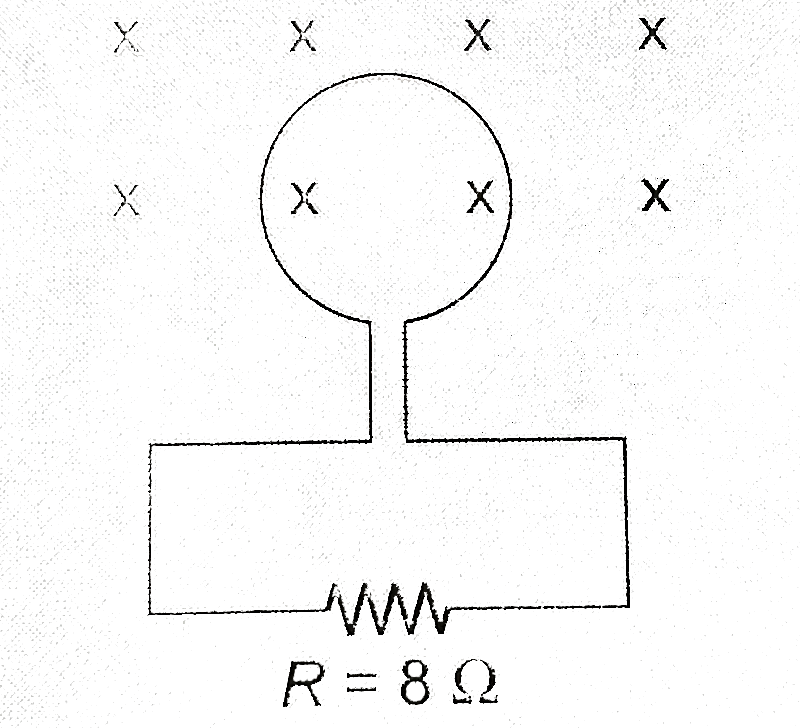 View Solution
View SolutionThe magnetic flux through a coil is varying according to the relation ϕ=(5t3+4t2+2t−5) Wb. Calculate the induced current through the coil at t=2 s if resistiance of coil is 5 ohm.
View SolutionThe magnetic flux through a loop varries according to the relation ∅ = 8t2+6t+2,∅ is in milliweber and t is in second. What is the magnitude of the induced emf in the loop
at t = 2 seconds?View SolutionThe magnetic flux thropugh a loop varies according to the relation ϕ=t2+6t+C, where 'C' is constant, ϕ is in milliwebe3r and 't' is in sedcond. What is the mognitude of induced e.m.f. in the loop at t = 2 seconds ?
View SolutionThe magnetic flux linked with a coil is ϕ=(4t2−6t−1) milliweber. Find the emf induced in the coil at t = 2 s
View Solution

