The magnitude and direction of the electric field at point P can be best represented by

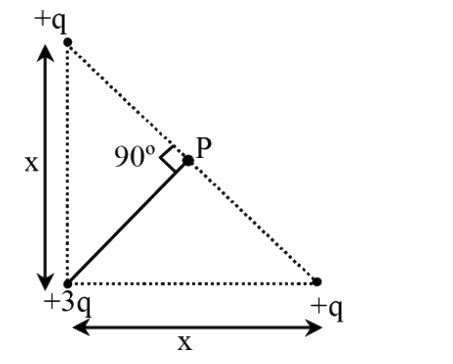
$\frac{3 k q}{x^{2}} (ˆ i + ˆ j)$

$\frac{\sqrt{2} k q}{x^{2}} (ˆ i + ˆ j)$

$\frac{3 \sqrt{2} k q}{x^{2}} (- ˆ i - ˆ j)$

$\frac{3 \sqrt{2} k q}{x^{2}} (ˆ i + ˆ j)$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Answer

Step by step video & image solution for The magnitude and direction of the electric field at point P can be best represented by by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Knowledge Check

Question 1 - Select One
The Electric field at a point is
Aalways continuous
Bcontinuous if there is no charge at that point
Cdiscontinuous if there is a charge at that point
Dboth (b) and ( c) are correct

Four long, parallel conductors carry equal currents of $5.0$ . The direction of the currents is into the pge at points. $A$ and $B$ and out of the page at $C$ and $D$ . Calculate the magnitude and directionof the mgnetic field at point $P$ , located at the centre of the square.

View Solution
Figure shows a set of equipotential surfaces. The magnitude and direction of electric field that exists in the region is-

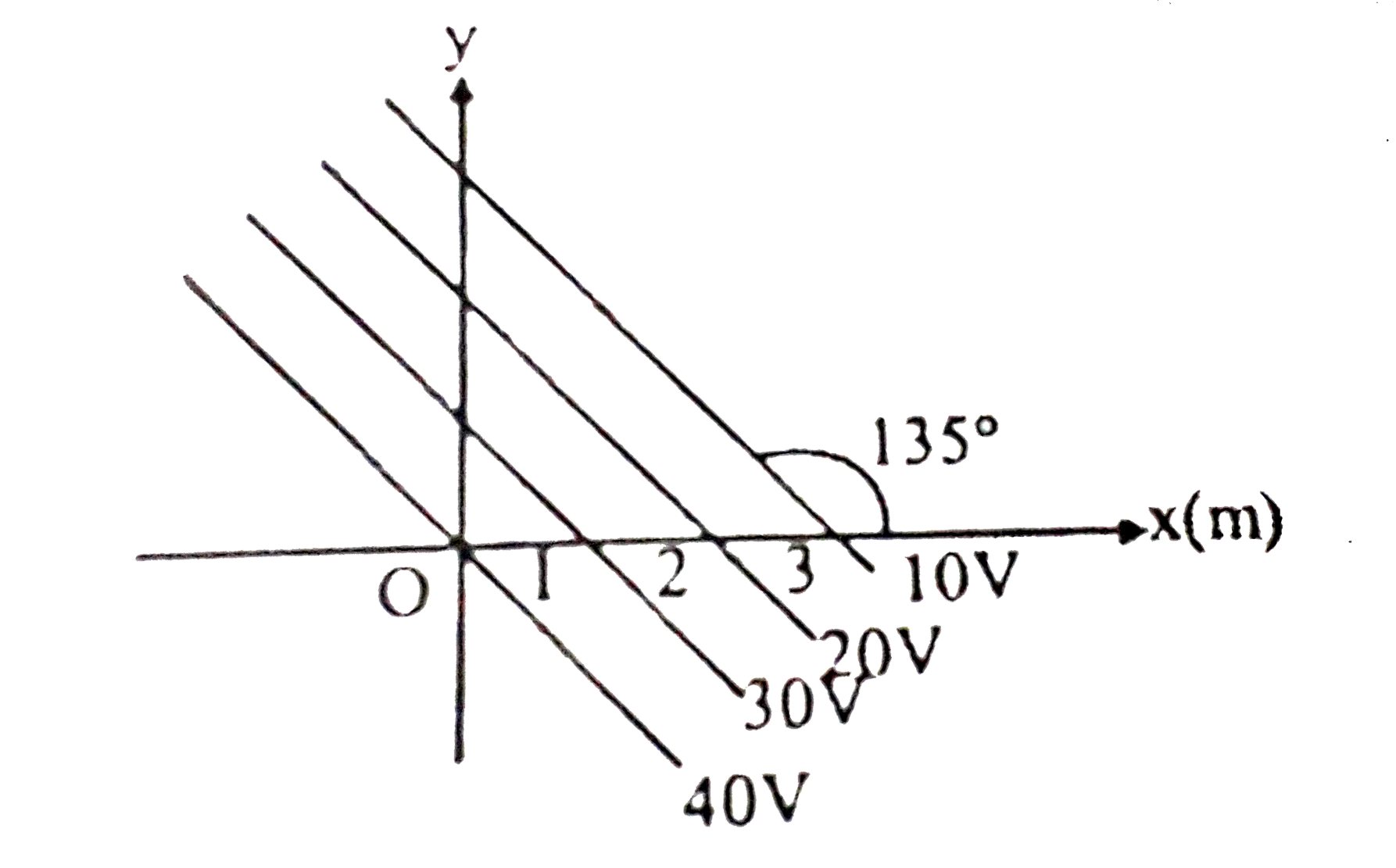
View Solution
Find the magnitude and direction of magnetic field at point P due to the current carrying wire as shown in

View Solution
Find the magnitude and direction of magnetic field at point O in the following case

View Solution
In a plane electromagnetic wave, the directions of electric field and magnetic field are represented by k and $2 ˆ i - 2 ˆ j$ , respectively. What is the unit vector along direction of propagation of the wave.
View Solution
A point charge Q is placed at the centre of a spherical conducting shell. A total charge of -q is placed on the shell. The magnitude of the electric field at point $P_{1}$ at a distance $R_{1}$ from the centre is X. The magnitude of the electric field due to induced charges at point $P_{2}$ a distance $R_{2}$ from the centre is Y. The values of X and Y are respectively.

View Solution
A uniform but time varying magnetic field $B (t)$ exist in a circular region of radius $a$ and is directed into the plane of the paper as shown. The magnitude of the induced electric field at point $P$ at a distance $r$ form the centre of the circular region.
View Solution

The magnitude and direction of the electric field at point P can be best represented by

The correct Answer is:D

Similar Questions

Knowledge Check

The Electric field at a point is

Recommended Questions