The magnitudes of the gravitational force at distances r1andr2 from the centre of a uniform sphere of radius R and mass M are F1andF2 respectively. Then (more than one are correct)
F1F2=r1r2 if r1<R and r2<R
r22r2 if r1>R and r2>R
F1F2=r1r2 if r1>R and r2>R
F1F2=r21r22 if r1<R and r2<R
The correct Answer is:A, B
For r>R, the gravitational field is F=GM/r2
∴F1=GMr31 and F2=GMr22⇒F1F2=r22R21
For r>>R
The gravitational field is F=GMR3×r
∴F1=GMR3×r1 and F2=GMR3×r2
⇒F1F2=r1r2
Topper's Solved these Questions
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - AR_TYPE
1 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - SCQ_TYPE
12 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
Similar Questions
The magnitude of the gravitational field at distance r1 and r2 from the centre of a uniform sphere of radius R and mass M are F1 and F2 respectively. Then:
View SolutionThe magnitude of the gravitational field at distance r1andr_2omthecentreofaunifromsphereofradiusRandmassmareF_1 and F_2 respectively. Then:
View SolutionThe magnitude of gravitational field at distances r1 and r2 from the centre of a uniform sphere of radius R and mass M, respectively. Find the ratio of (I1)/(I2)) if r1>R and r2>R.
View SolutionA point charge q , is placed at a distance r from the centre of an aluminium sphere, of radius R (r>R) . Selectr the correct alternatives.
View SolutionThe gravitational potential energy of a body at a distance r from the centre of earth is U. Its weight at a distance 2r from the centre of earth is
View SolutionThe work done by gravitational force on a point mass m0in moving from the surface of a planet off mass M and radius R to a height R2 is
View SolutionTwo identical thin ring each of radius R are co-axially placed at a distance R. If the ring have a uniform mass distribution and each has mass m1 and m2 respectively, then the work done in moving a mass m from the centre of one ring to that of the other is :
View SolutionThe gravitational potential at a point outside the solid sphere of radius "R" and at a distance of "r" will be :
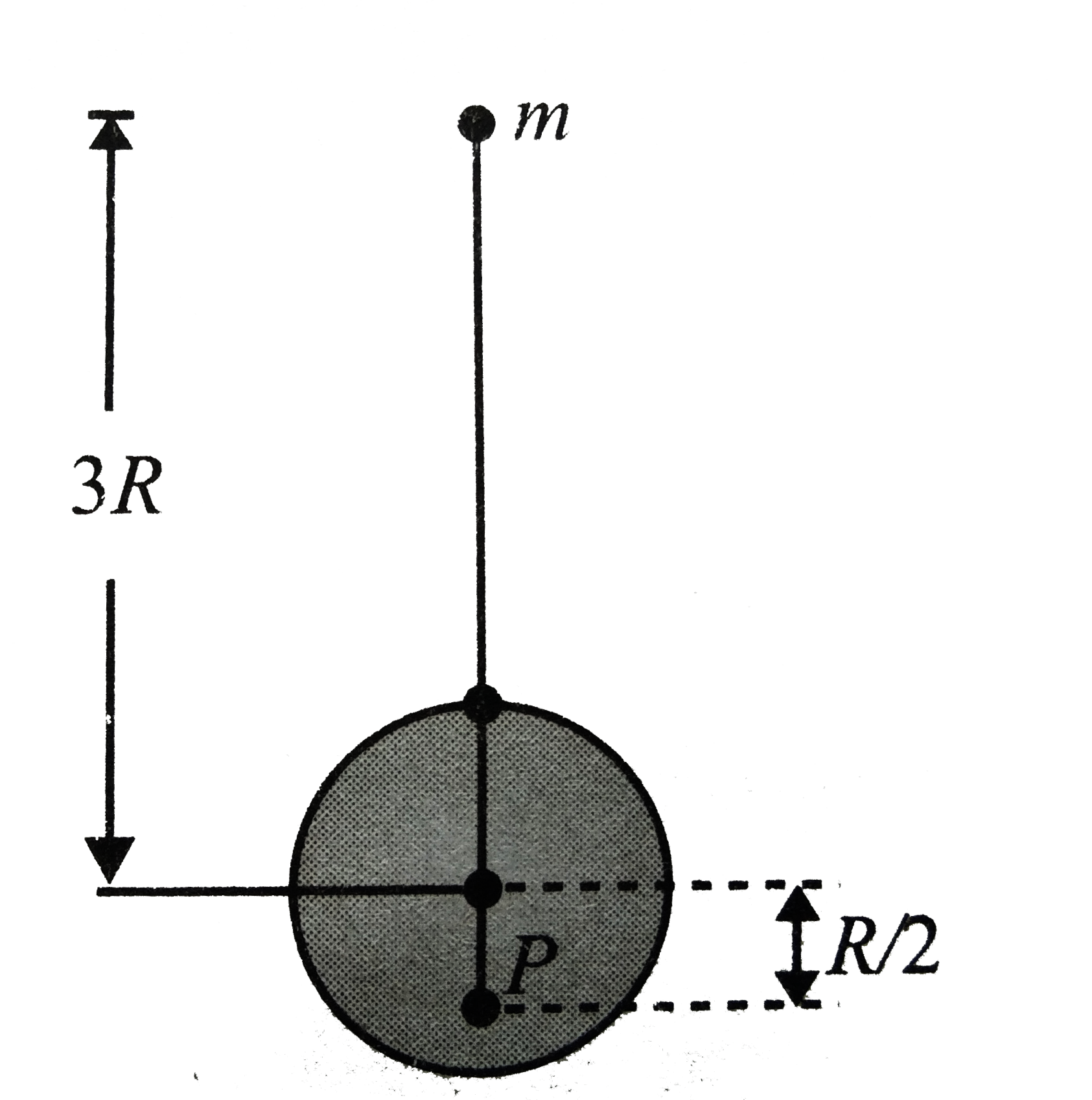
View SolutionA point mass m is released from rest at a distance of 3R from the centre of a thin-walled hollow sphere of radius R and mass M as shown. The hollow sphere is fixed in position and the only force on the point mass is the gravitational attraction of the hollow sphere. There is a very small hole in the hollow sphere through which the point mass falls as shown. The velocity of a point mass when it passes through point P at a distance R/2 from the centre of the sphere is
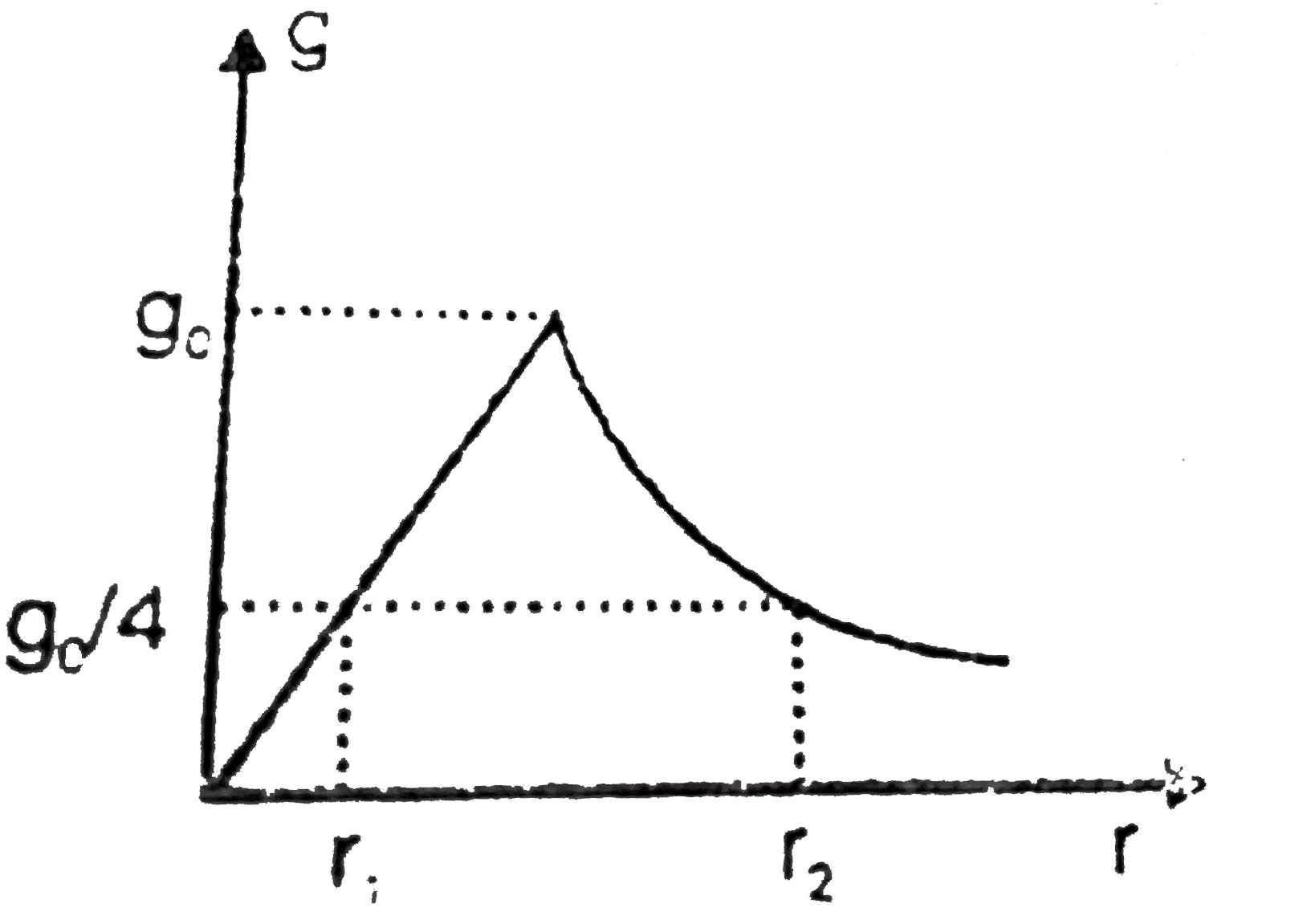
View SolutionFigure shows variation of acceleration due to gravity with distance from centre of a uniform spherical planet, Radius of planet is R. What is r1−r1
View Solution
