The gravitational potential at a point outside the solid sphere of radius "R" and at a distance of "r" will be :
linearly dependent on r
proportional to 1r
proportional to r2
same everywhere
The correct Answer is:A
To find the gravitational potential at a point outside a solid sphere of radius R and at a distance r from the center of the sphere, we can follow these steps:
1. Understanding Gravitational Potential:
The gravitational potential V at a distance r from a mass M is given by the formula:
V=−GMr
where G is the gravitational constant.
2. Identifying the Mass of the Sphere:
For a solid sphere of radius R and mass M, when we are outside the sphere (i.e., at a distance r such that r>R), the sphere can be treated as if all its mass were concentrated at its center.
3. Applying the Formula:
Since we are considering a point outside the sphere, we can substitute M (the mass of the sphere) into the gravitational potential formula:
V=−GMr
4. Conclusion:
Thus, the gravitational potential at a point outside the solid sphere at a distance r from its center is:
V=−GMr
This shows that the gravitational potential depends inversely on the distance r.
Final Answer:
The gravitational potential at a point outside the solid sphere of radius R and at a distance r is given by:
V=−GMr
The gravitational potential V at a distance r from a mass M is given by the formula:
V=−GMr
where G is the gravitational constant.
For a solid sphere of radius R and mass M, when we are outside the sphere (i.e., at a distance r such that r>R), the sphere can be treated as if all its mass were concentrated at its center.
Since we are considering a point outside the sphere, we can substitute M (the mass of the sphere) into the gravitational potential formula:
V=−GMr
Thus, the gravitational potential at a point outside the solid sphere at a distance r from its center is:
V=−GMr
This shows that the gravitational potential depends inversely on the distance r.
The gravitational potential at a point outside the solid sphere of radius R and at a distance r is given by:
V=−GMr
Topper's Solved these Questions
- GRAVITATIONBOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - EXERCISE-2 PART-2
10 Videos
- GRAVITATIONBOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - EXERCISE-2 PART-3
12 Videos
- GRAVITATIONBOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - EXERCISE-1 PART-3
2 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Advance level Problems
35 Videos
- NUCLEAR PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Advanced level solutions
16 Videos
Similar Questions
Gravitational field at the surface of a solid sphere is 1.5×10−4N kg−1. Find the gravitational field at a point situated inside the sphere at a distance equal to half of rhe radius of the solid sphere.
View Solution
Statement I: The magnitude of the gravitational potential at the surface of solid sphere is less than that of the centre of sphere. Statement II: Due to the solid sphere, the gravitational potential is the same within the sphere.
View SolutionBy which curve will be variation of gravitational potential of a hollow sphere of radius R with distance be depicted ?
View SolutionThe radius of gyration of a solid sphere of radius R about its tangent is
View SolutionThe distance between the centres of the Moon and the earth is D. The mass of the earth is 81 times the mass of the Moon. At what distance from the centre of the earth, the gravitational force will be zero?
View SolutionThe magnitude of the gravitational field at distance r1andr_2omthecentreofaunifromsphereofradiusRandmassmareF_1 and F_2 respectively. Then:
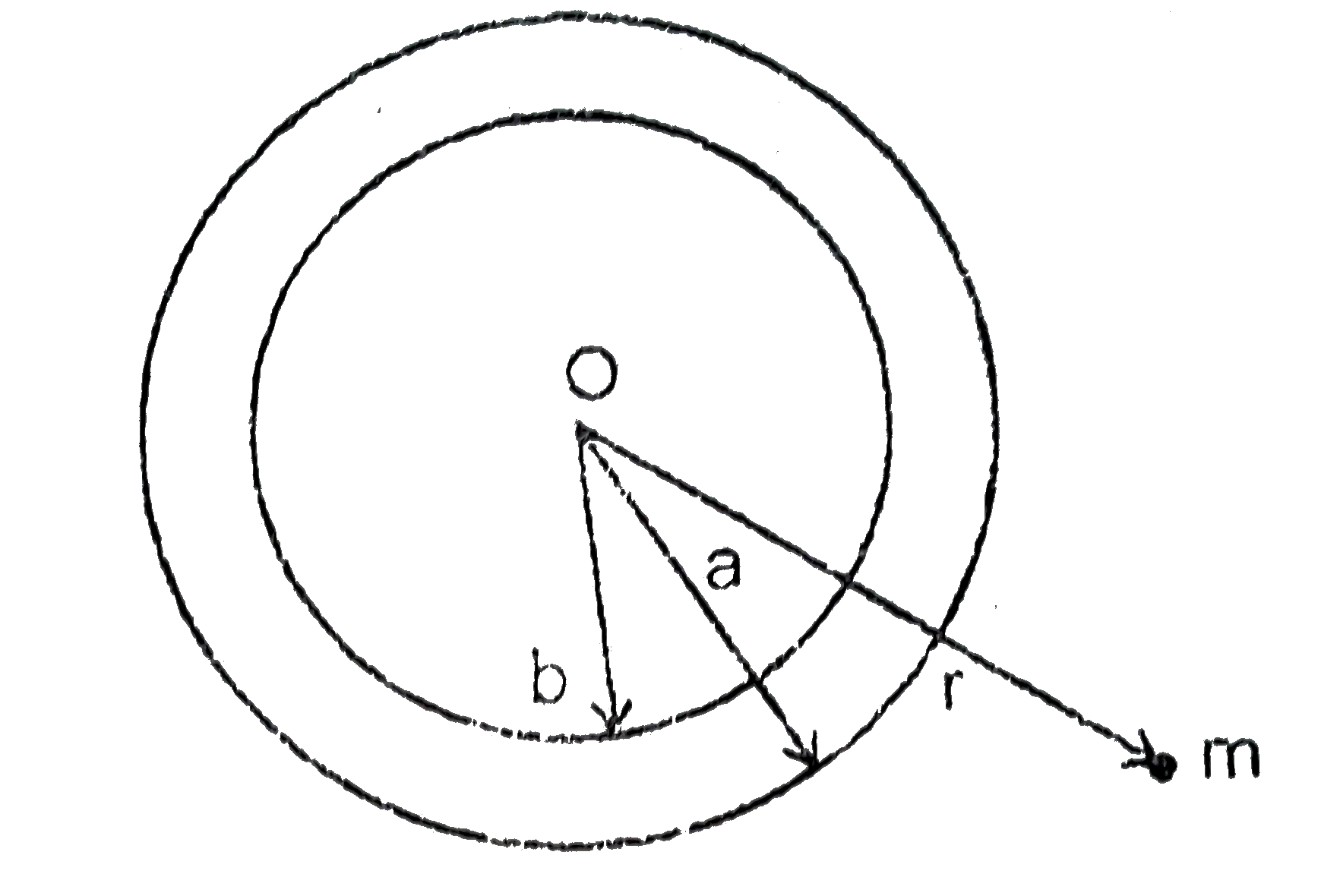
View SolutionA sphere of density ρ and radius a has a concentric of radius b as shown in the
(a) Sketch the gravitational force exerted by the spehre on the particle of mass m located at a distance r from the centre of the sphere as a function of r in the range 0≤r≤∞
(b) Sketch the corresponding curve for the potential energy u (r) of the system
 ,
,
View SolutionPotential at a point x-distance from the centre inside the conducting sphere of radius R and charged with charge Q is
View SolutionFind the gravitational potential due to a spherical shell of mass M and radius R at r<R and r>R, where r is the distance from the centre of the shell.
View SolutionIn the figure shown a conducting sphere of inner radius 'a' and outer radius 'b' is given a charge Q. A point charge 'q' is placed in the cavity of this sphere at distance 'x'(<a) away from the centre. Find the electric field intensity and electric potentials at point P (outside the sphere) at distance r>b. Also find the electric potential at point C

View Solution
