The mass of a body cannot be considered to be concentrated at the centre of mass of the body for the purpose of computing its moment of inertia.
For then the moment of inertia of every body about an axis passing through its centre of mass would be zero.
Statement I is True, Statement II is True, Statement ll is a correct explanation for Statement I.
Statement I is True, Statement II is True, Statement II is NOT a correct explanation for Statement I
Statement I is True, Statement II is False.
Statement I is False, Statement II is True.
The correct Answer is:A
To solve the question, we need to analyze the statements regarding the moment of inertia and the center of mass of a body.
1. Understanding the Concept of Moment of Inertia:
- Moment of inertia (I) is a measure of an object's resistance to changes in its rotation about an axis. It depends on the mass distribution of the body relative to the axis of rotation.
- The formula for the moment of inertia about an axis is given by:
I=∑mir2i
where mi is the mass of the individual particles and ri is the distance of each mass from the axis of rotation.
2. Center of Mass and Its Implications:
- The center of mass (CM) of a body is the point where the mass of the body can be considered to be concentrated for translational motion.
- However, for rotational motion, the mass distribution relative to the axis of rotation is crucial.
3. Analyzing the First Statement:
- The first statement claims that the mass of a body cannot be considered to be concentrated at the center of mass for the purpose of computing its moment of inertia.
- This is true because if we consider the entire mass at the center of mass, the distances ri from the axis of rotation would all be zero, leading to:
I=∑mi⋅02=0
- Therefore, the first statement is correct.
4. Analyzing the Second Statement:
- The second statement says that if we consider the mass concentrated at the center of mass, then the moment of inertia about an axis passing through the center of mass would be zero.
- This is also true for the same reason as above; if all mass is concentrated at the center of mass, the distances from the axis of rotation would again be zero, resulting in:
I=0
- Thus, the second statement is also correct.
5. Conclusion:
- Both statements are correct. The mass cannot be treated as concentrated at the center of mass when calculating the moment of inertia, as it would lead to a moment of inertia of zero for any axis through the center of mass.
Final Answer:
Both statements are correct.
---
- Moment of inertia (I) is a measure of an object's resistance to changes in its rotation about an axis. It depends on the mass distribution of the body relative to the axis of rotation.
- The formula for the moment of inertia about an axis is given by:
I=∑mir2i
where mi is the mass of the individual particles and ri is the distance of each mass from the axis of rotation.
- The center of mass (CM) of a body is the point where the mass of the body can be considered to be concentrated for translational motion.
- However, for rotational motion, the mass distribution relative to the axis of rotation is crucial.
- The first statement claims that the mass of a body cannot be considered to be concentrated at the center of mass for the purpose of computing its moment of inertia.
- This is true because if we consider the entire mass at the center of mass, the distances ri from the axis of rotation would all be zero, leading to:
I=∑mi⋅02=0
- Therefore, the first statement is correct.
- The second statement says that if we consider the mass concentrated at the center of mass, then the moment of inertia about an axis passing through the center of mass would be zero.
- This is also true for the same reason as above; if all mass is concentrated at the center of mass, the distances from the axis of rotation would again be zero, resulting in:
I=0
- Thus, the second statement is also correct.
- Both statements are correct. The mass cannot be treated as concentrated at the center of mass when calculating the moment of inertia, as it would lead to a moment of inertia of zero for any axis through the center of mass.
Both statements are correct.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension71videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Integer7videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Single Correct142videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
Can mass of a body be taken concentrated at its centre of mass for the purpose of calculating its rotational inertia ?
View SolutionThe moment of inertia of a body about a given axis of rotation depends upon :-
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionThe moment of inertia of a cube of mass M and edge length a about an axis passing through one of its edge is
View Solutionfind moment of inertia about an axis yy which passes through the centre of mass of the two particle system as shown
 View Solution
View SolutionThe moment of inertia of a hollow cubical box of mass M and side a about an axis passing through the centres of two opposite faces is equal to.
View SolutionIn the figure shown ABCD is a lamina of mass 12kg. The moment of inertia of the given body about an axis passing through D, and perpendicular to the plane of the body is
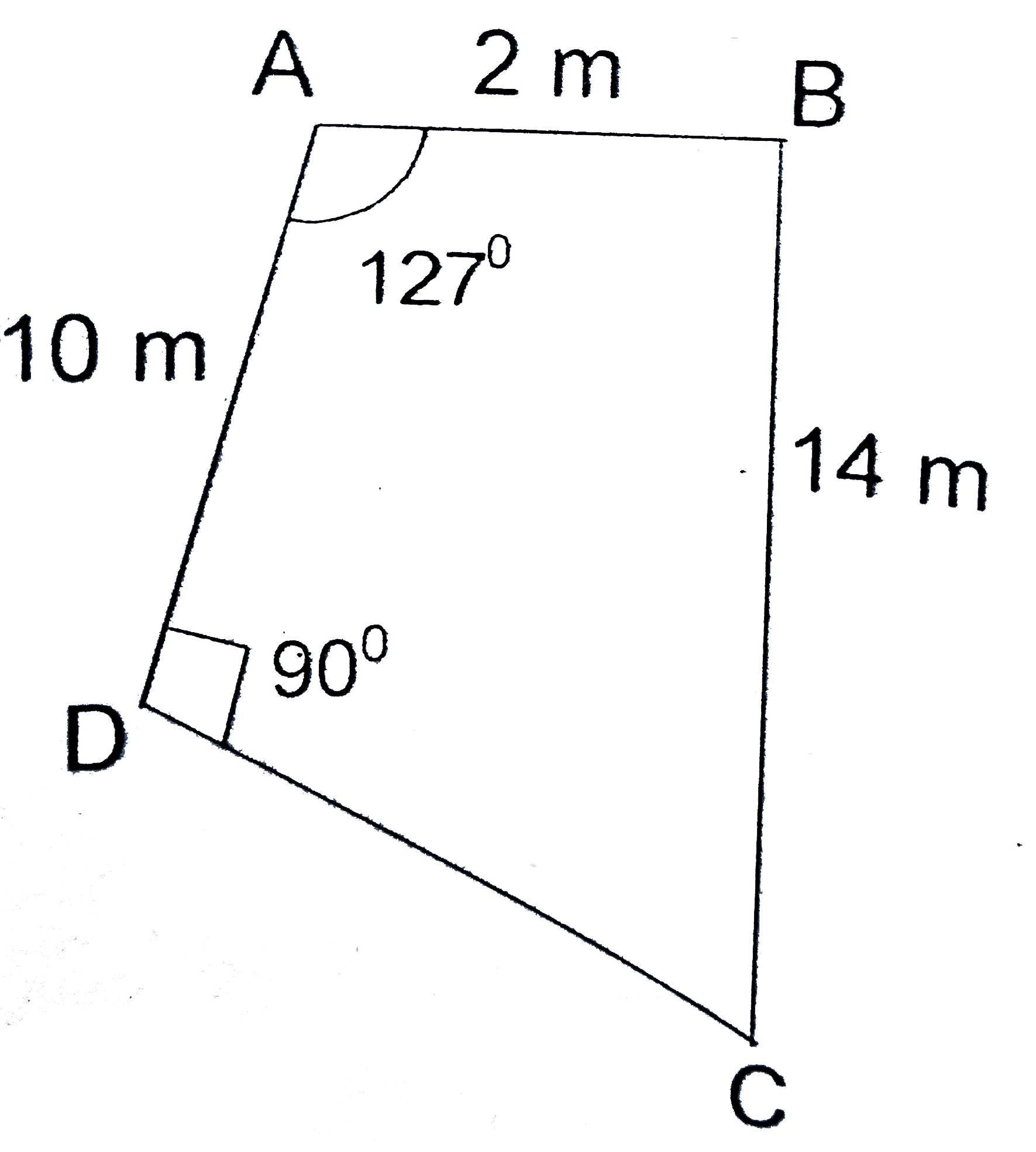 View Solution
View SolutionFor calculating the moment of inertia of a body can we assume the whole mass of the body to be concentrated at its centre of mass ?
View SolutionCalculate the moment of inertia of a ring of mass 2kg and radius 2cm about an axis passing through its centre and perpendicular to its surface.
View SolutionCalculate the moment of inertia of a ring of mass 2kg and radius 2cm about an axis passing through its centre and perpendicular to its surface.
View Solution
