The Maxwell-Boltzmann distribution of molecular speeds in a sample of an ideal gas can be expressed as
Where f represent the fraction of total molecules that have speeds between v and v + dv.m, k and T are mass of each molecule, Boltzmann constant and temperature of the gas.
(a) What will be value of
(b) It is given that
Find the average speed of gas molecules at temperature T.
The correct Answer is:(a) 1 " "
Step by step video, text & image solution for The Maxwell-Boltzmann distribution of molecular speeds in a sample of an ideal gas can be expressed as f=(4)/(sqrt(pi))((m)/(2kT))^(3//2)v^(2)e^(-(mv^(2))/(2kT)).dv Where f represent the fraction of total molecules that have speeds between v and v + dv.m, k and T are mass of each molecule, Boltzmann constant and temperature of the gas. (a) What will be value of int_(v=0)^(v=oo)fdv ? (b) It is given that int_(0)^(oo) v^(3)e^(-av^(2))dv=(1)/(2a^(2)) Find the average speed of gas molecules at temperature T. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINETIC THEORY OF GASESBOOK - ARIHANTCHAPTER - KINETIC THEORY OF GASESEXERCISE - Level 3
4 Videos
- KINETIC THEORY OF GASESBOOK - ARIHANTCHAPTER - KINETIC THEORY OF GASESEXERCISE - Level 3
4 Videos
- KINEMATICSBOOK - ARIHANTCHAPTER - KINEMATICSEXERCISE - Level 3
33 Videos
- MOMENTUM AND CENTRE OF MASSBOOK - ARIHANTCHAPTER - MOMENTUM AND CENTRE OF MASSEXERCISE - Momentum And Center of Mass
117 Videos
Similar Questions
An ideal gas is inside a cylinder with a piston that can move freely. The walls of the cylinder and piston are non- conducting. The piston is being moved out of the cyl- inder at a constant speed u.
(a) Consider a gas molecule of mass m moving with speed v(>>u). It hits the piston elastically at an angle of incidence q. Calculate the loss in kinetic energy of the molecule.
(b) If the area of piston is A and pressure of the gas is P, calculate the rate of decreases of molecular kinetic energy of the gas sample.
(c) Ifu>> molecular velocities, at what rate will the gas lose its molecular kinetic energy
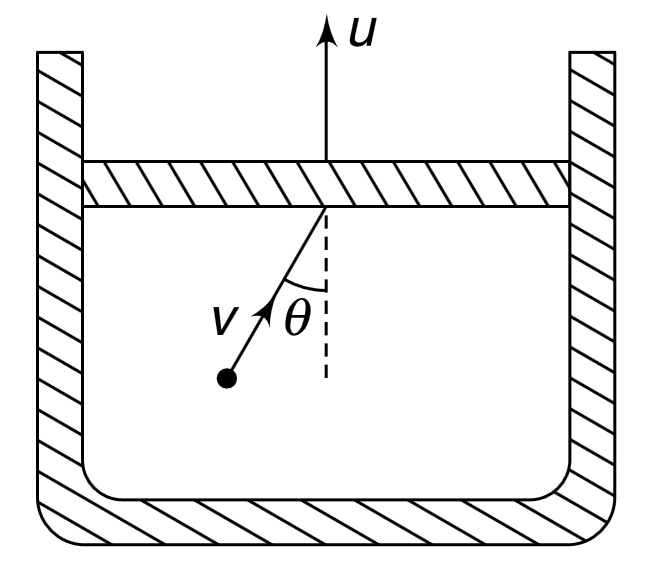
View SolutionAn ideal gas is inside a cylinder with a piston that can move freely. The walls of the cylinder and piston are non- conducting. The piston is being moved out of the cyl- inder at a constant speed u.
(a) Consider a gas molecule of mass m moving with speed v(>>u). It hits the piston elastically at an angle of incidence q. Calculate the loss in kinetic energy of the molecule.
(b) If the area of piston is A and pressure of the gas is P, calculate the rate of decreases of molecular kinetic energy of the gas sample.
(c) Ifu>> molecular velocities, at what rate will the gas lose its molecular kinetic energy

View SolutionA car manufacturer usually tells a optimum speed (V0) at which the car should be driven to get maximum mileage. In order to find the optimum speed for a new model, an engineer of the car company experimented a lot and finally plotted a graph between the extreme time t (defined as number of hours a tank full of petrol lasts) vs the constant speed V at which car was run.
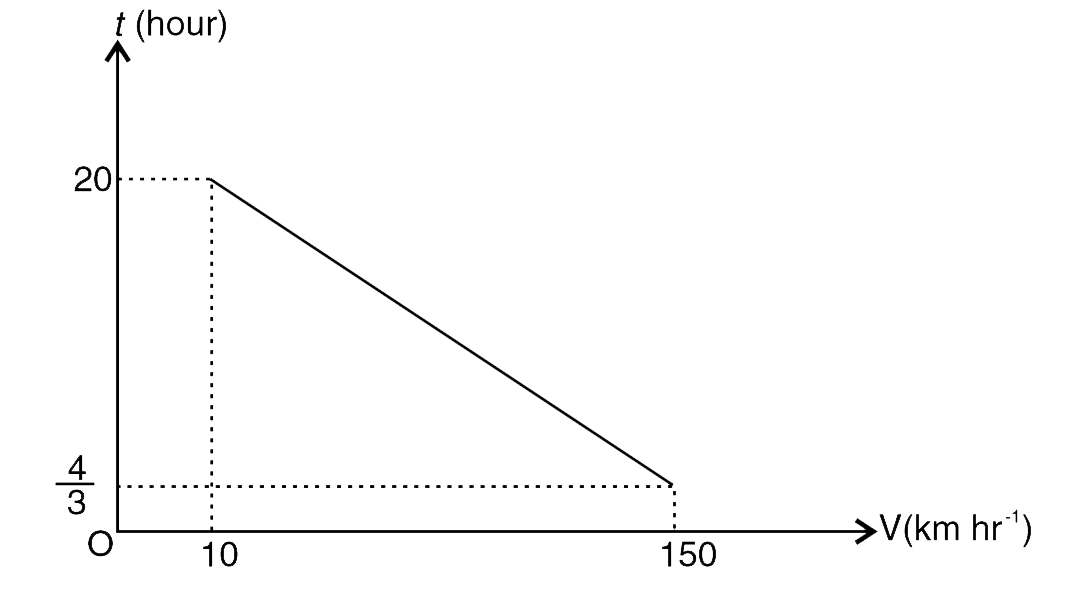
(a) Calculate the optimum speed V0 for this new model.
(b) If the fuel tank capacity of this car is 50 litre, what maximum mileage can be obtained from this car?
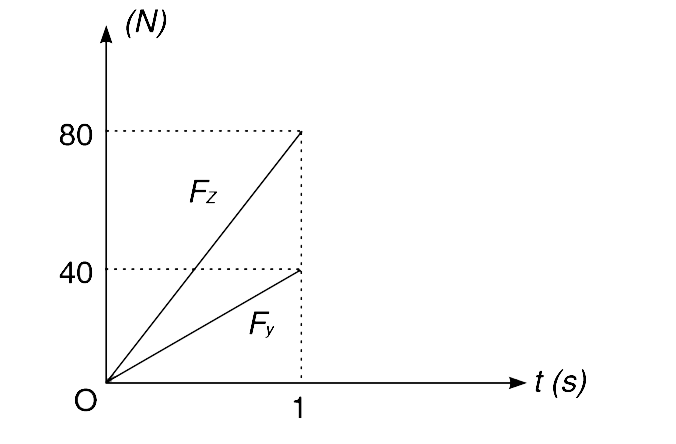
View SolutionA particle is acted upon by a force for 1 second whose X component remains constant at Fx=30N but y and z components vary with time as shown in the graph. Calculate the magnitude of change in momentum of the particle in 1 s. What angle does the change in momentum (Δ→P) make with X axis ?
View SolutionThe distribution of the molecular velocities of gas molecules at any temperature T is shown below. (The plot below is known as Maxwell's distribution of molecular speeds.)

where
v is molecular velocity
n is number of molecules having velocity v
Let us define ΔNv, which is equal to the number of molecules between the velocity range v and v+Δv, given by
ΔNv=4πNa3e−bv2v2Δv
where
N is total number of molecules
a=√M02πRT and b=M02RT
R is universal gas constant
T is temperature of the gas
M0 is molecular weight of the gas
Answer the following question:
If PPc=Pr, TTc=Tr, and VmVm,c=Vr where
View SolutionFor a gas sample with N_(0) number of molecules, function N(V) is given by: N(V) = (dN)/(dV) = ((3N_(0))/(V_(0)^(3)))V^(2) for 0 lt V lt V_(0) and N(V) = 0 for V gt V_(0) . Where dN is number of molecules in speed range V to V+ dV . The rms speed of the molecules is:
View SolutionAccording to Maxwell - distribution law, the probability function representing the ratio of molecules at a particular velocity to the total number of molecules is given by f(v)=k_(1)sqrt(((m)/(2piKT^(2))))4piv^(2)e^(-(mv^(2))/(2KT)) Where m is the mass of the molecule, v is the velocity of the molecule, T is the temperature k and k_(1) are constant. The dimensional formulae of k_(1) is
View SolutionA vessel of volume V contains a mixture of 1 mole of hydrogen and 1 mole oxygen (both considered as ideal). Let f_(1)(v) dv, denote the fraction of molecules with speed between v and (v+ dv) with f_(2)(v)dv , similarly for oxygen . Then ,
View SolutionA ideal gas has pressure 'p', volume 'V' and absolute temperature 'T'. It 'm' is the mass of each molecules and 'K' is the Boltzmann constant , the density of the gas is
View SolutionIf P is the pressure,V the volume,R the gas constant,k the Boltzmann constant and T the absolute temperature,then number of molecules in the given mass of the gas is given
View SolutionClaim: Maxwell - Boltzmann can calculate the number of molecules in the velocity range v from v + dv using the velocity function. Reason: There is no change in the area of the map because the area of the map is equal to the total number of gas molecules.
View SolutionA vessel of volume V contains a mixture of 1 mole of hydrogen and 1 mole oxygen (both considered as ideal). Let f1(v)dv, denote the fraction of molecules with speed between v and (v+ dv) with f2(v)dv, similarly for oxygen . Then ,
View SolutionA vessel of volume V contains a mixture of 1 mole of hydrogen and 1 mole oxygen (both considered as ideal). Let f_(1)(v) dv, denote the fraction of molecules with speed between v and (v+ dv) with f_(2)(v)dv , similarly for oxygen . Then ,
View SolutionAssume a sample of gas in a vessel. The speeds of molecules are between 2 m/s. to 5m/s. The number of molecules for speed v (m/s) is given by n=7v - v^(2) - 10 . The most probable speed in the sample is
View SolutionFor a gas sample with N0 number of molecules, function N(v) is given by : N(v)=dNdv=(3N0v30)v2 for 0<v<v0andN(v)=0 for v>v0, where dN is number of molecules in speed range v to v+dv. Find the rms speed of the molecules.
View Solution
