The minimum and maximum distances of a satellite from the center of the earth are 2R and 4R respectively, where R is the radius of earth and M is the mass of the earth . Find
(a) its minimum and maximum speeds,
(b) radius of curvature at the point of minimum distance.
√8R3
√5R3
√4R3
√7R3
The correct Answer is:A
Applying the principle of conservation of angular momentum,
mv1(2R)=mv2(4R)
v1=2v2……i
From conservation of energy
12mv21−GMm2R=12mv22−GMm4R……….ii
Solving eqn i and ii we get
v2=√GM6R,v1=√2GM3R
If r is the radius of curvature at point A. 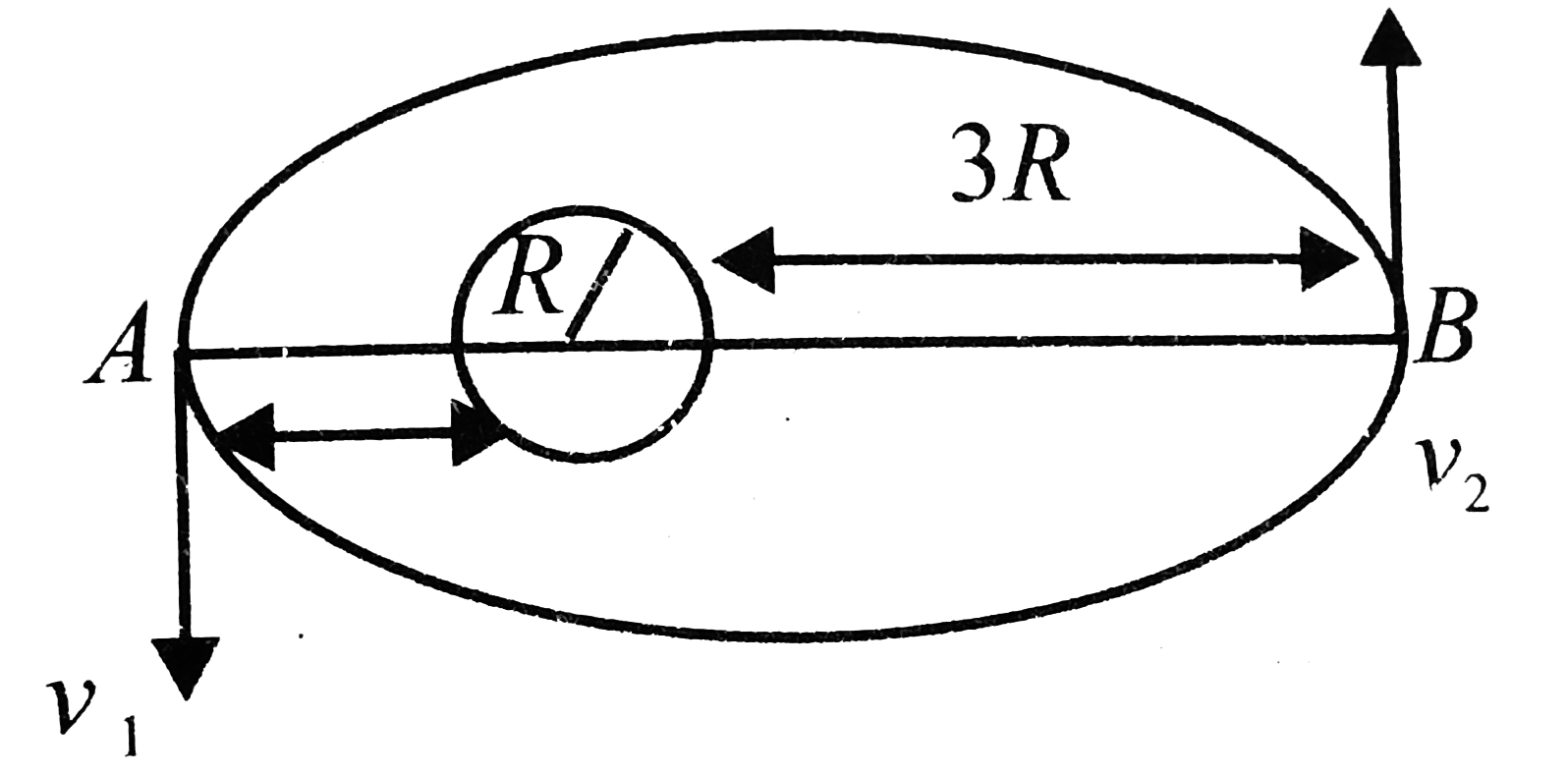
mv21r=GMm(2R)2
r=4v21GM=8R3 (putting value of v1)
Topper's Solved these Questions
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Integer
5 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Fill In The Blanks
5 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Assertion- Reasoning
13 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
Similar Questions
The minimum and maximum distance of a satellite from the centre of the earth are 2R and 4R respectively, where R is the radius of earth and M is the mass of the earth. The radius of curvature at the point of maximum distance is
View SolutionThe distance of geostationary satellite from the centre of the earth (radius R) is nearest to
View Solution
Knowledge Check
The escape velocity from the surface of the earth is (where RE is the radius of the earth )
A√2gREB√gREC2√gRED√3gRE
Two identical satellites are moving around the Earth in circular orbits at heights 3R and R respectively where R is the radius of the Earth. The ratio of their kinetic energies is x. Find x.
View SolutionThe radii of circular orbits of two satellite A and B of the earth are 4R and R, respectively. If the speed of satellite A is 3v, then the speed of satellite B will be
View SolutionTwo satellites A and B of the same mass are orbiting the earth at altitudes R and 3R respectively, where R is the radius of the earth. Taking their orbit to be circular obtain the ratios of their kinetic and potential energies.
View SolutionThe potential energy of a satellite of mass m revolving at height R above the surface of the earth where R= radius of earth is
View SolutionA satellite of mass m goes round the earth along a circular path of radius r. Let mE be the mass of the earth and RE its radius then the linear speed of the satellite depends on.
View SolutionTwo identical satellites are orbiting are orbiting at distances R and 7R from the surface of the earth, R being the radius of the earth. The ratio of their
View SolutionIf body of mass mhas to be taken from the surface to the earth to a height h=4R, then the amount of energy required is (R = radius of the earth)
View Solution
