The moment of inertia of a door of mass m, length 2l and width l about its longer side is.
11ml224
5ml224
ml23
none of these
The correct Answer is:C
(About YYh) =ml212
Using parallel axis theorem,
I (about AD) =ml212+ml24=ml23

Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Linked Comprehension
28 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective
13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
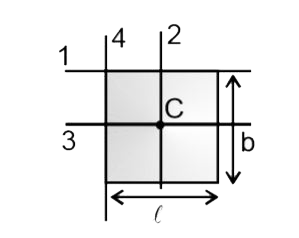
In the figure shown find moment of inertia of a plate having mass M, length l and width b about axis 1,2,3 and 4. Assume that C is centre and mass is uniformly distributed
View SolutionWhat is moment of inertia of a solid cylinder of mass m, length l and radiusr about the axis of the cylinder ?
View Solution
Knowledge Check
The moment of inertia of a uniform cylinder of length landradiusR about its perpendicular bisector is I. What is the ratio l/R such that the moment of inertia is minimum ?
A1B3√2C√32D√32Moment of inertia of a cylinder of mass M, length L and radius R about an axis passing through its centre and perpendicular to the axis of the cylinder is I=M(R24+L212). If such a cylinder is to be made for a given mass of a material, the ratio L/R for it to have minimum possible I is :
A23B32C√23D√32The moment of inertia of a cube of mass m and side a about one of its edges is equal to
A23ma2B43ma2C3ma2D83ma2
Calculate moment of inertia of a square of each side of mass m, length l about a corner and perpendicular to plane.
View SolutionThe moment of inertia of a cylinder of radius R, length L and mass M about an axis passing through its centre of mass and normal to its length is
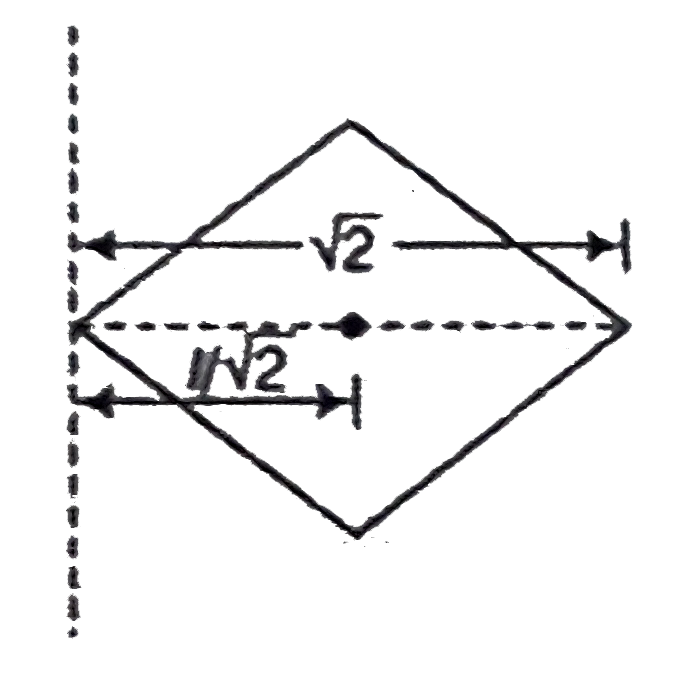
View SolutionThe moment of inertia of a system of four rods each of length l and mass m about the axis shown is
View SolutionThe moment of inertia of a uniform rod of length 2l and mass m about an axis xy passing through its centre and inclined at an angle α is

View SolutionMoment of inertia of a rod of mass m and length l about its one end is l. If one-fourth of its length is cur away, then moment of inertia of the remaining rod about its one end will be
View Solution
